Swipe Bo
Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)Total Submission(s): 1654 Accepted Submission(s): 337
Problem Description
“Swipe Bo” is a puzzle game that requires foresight and skill.
The main character of this game is a square blue tofu called Bo. We can swipe up / down / left / right to move Bo up / down / left / right. Bo always moves in a straight line and nothing can stop it except a wall. You need to help Bo find the way out.
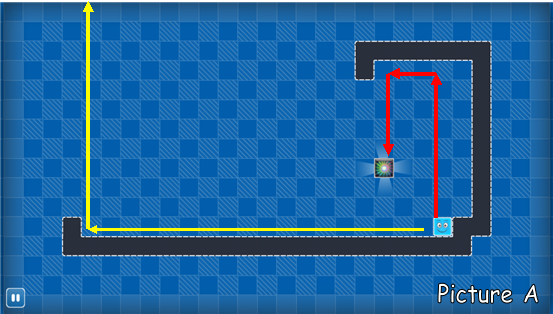
The picture A shows that we needs three steps to swipe Bo to the exit (swipe up, swipe left, swipe down). In a similar way, we need only two steps to make Bo disappear from the world (swipe left, swipe up)!
Look at the picture B. The exit is locked, so we have to swipe Bo to get all the keys to unlock the exit. When Bo get all the keys, the exit will unlock automatically .The exit is considered inexistent if locked. And you may notice that there are some turning signs, Bo will make a turn as soon as it meets a
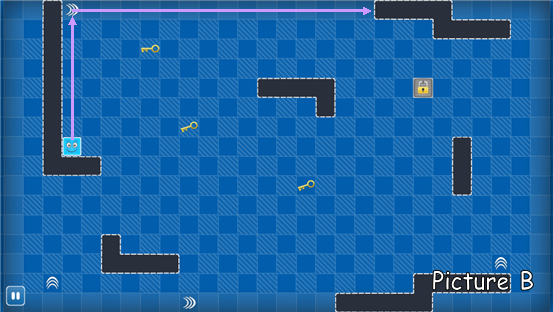
turning signs. For example, if we swipe Bo up, it will go along the purple line.
Now, your task is to write a program to calculate the minimum number of moves needed for us to swipe Bo to the exit.
The main character of this game is a square blue tofu called Bo. We can swipe up / down / left / right to move Bo up / down / left / right. Bo always moves in a straight line and nothing can stop it except a wall. You need to help Bo find the way out.
The picture A shows that we needs three steps to swipe Bo to the exit (swipe up, swipe left, swipe down). In a similar way, we need only two steps to make Bo disappear from the world (swipe left, swipe up)!

Look at the picture B. The exit is locked, so we have to swipe Bo to get all the keys to unlock the exit. When Bo get all the keys, the exit will unlock automatically .The exit is considered inexistent if locked. And you may notice that there are some turning signs, Bo will make a turn as soon as it meets a

turning signs. For example, if we swipe Bo up, it will go along the purple line.
Now, your task is to write a program to calculate the minimum number of moves needed for us to swipe Bo to the exit.
Input
The input contains multiple cases, no more than 40.
The first line of each test case contains two integers N and M (1≤N, M≤200), which denote the sizes of the map. The next N lines give the map’s layout, with each line containing M characters. A character is one of the following: '#': represents the wall; 'S' represents the start point of the Bo; 'E' represents the exit; '.' represents an empty block; ‘K’ represents the key, and there are no more than 7 keys in the map; 'L','U','D','R' represents the turning sign with the direction of left, up, down, right.
The first line of each test case contains two integers N and M (1≤N, M≤200), which denote the sizes of the map. The next N lines give the map’s layout, with each line containing M characters. A character is one of the following: '#': represents the wall; 'S' represents the start point of the Bo; 'E' represents the exit; '.' represents an empty block; ‘K’ represents the key, and there are no more than 7 keys in the map; 'L','U','D','R' represents the turning sign with the direction of left, up, down, right.
Output
For each test case of the input you have to calculate the minimal amount of moves which are necessary to make Bo move from the starting point to the exit. If Bo cannot reach the exit, output -1. The answer must be written on a single line.
Sample Input
5 6 ###### #....# .E...# ..S.## .##### 5 6 ###### #....# .....# SEK.## .##### 5 6 ###### #....# ....K# SEK.## .##### 5 6 ###### #....# D...E# S...L# .#####
Sample Output
3 2 7 -1
Source
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <vector>
#include <queue>
#include <set>
#include <algorithm>
#define LL long long
using namespace std;
const int MAXN = 200 + 2;
struct Node
{
int x, y;
int key;
int step;
};
char mp[MAXN][MAXN];
bool vis[MAXN][MAXN][1<<7][4];
bool use[MAXN][MAXN][1<<7];
int sx, sy, ex, ey;
int key_s[MAXN][MAXN];
int n, m;
int num_key;
int dir[][2] = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};
int bfs()
{
queue<Node>Q;
while(!Q.empty()) Q.pop();
memset(vis, false, sizeof(vis));
memset(use, false, sizeof(use));
Node now, nxt;
now.x = sx; now.y = sy;
now.key = 0; now.step = 0;
Q.push(now);
use[sx][sy][0] = true;
while(!Q.empty())
{
now = Q.front();
Q.pop();
for(int i=0;i<4;i++)
{
int x = now.x;
int y = now.y;
int key = now.key;
int mx = dir[i][0];
int my = dir[i][1];
while(1){
if(mp[x][y] == 'L')
{
mx = 0;
my = -1;
}
if(mp[x][y] == 'R')
{
mx = 0;
my = 1;
}
if(mp[x][y] == 'U')
{
mx = -1;
my = 0;
}
if(mp[x][y] == 'D')
{
mx = 1;
my = 0;
}
int dir;
if(mx == -1 && my == 0) dir = 0;
else if(mx == 1 && my == 0) dir = 1;
else if(mx == 0 && my == 1) dir = 2;
else if(mx == 0 && my == -1) dir = 3;
if(vis[x][y][key][dir]) break;
vis[x][y][key][dir] = true;
x += mx;
y += my;
if(x < 0 || x >= n || y < 0 || y >= m) break;
if(mp[x][y] == '#') break;
if(x == ex && y == ey && key == (1 << num_key) - 1)
return now.step + 1;
if(mp[x][y] == 'L')
{
mx = 0;
my = -1;
}
if(mp[x][y] == 'R')
{
mx = 0;
my = 1;
}
if(mp[x][y] == 'D')
{
mx = 1;
my = 0;
}
if(mp[x][y] == 'U')
{
mx = -1;
my = 0;
}
if(mp[x][y] == 'K')
key |= key_s[x][y];
if(x + mx >= 0 && x + mx < n && y + my>= 0 && y + my < m && mp[x+mx][y+my] =='#')
{
if(use[x][y][key]) break;
nxt.x = x;
nxt.y = y;
nxt.step = now.step + 1;
nxt.key = key;
Q.push(nxt);
use[x][y][key] = true;
break;
}
}
}
}
return -1;
}
int main()
{
while(scanf("%d%d", &n, &m)!=EOF)
{
//memset(key_s, 0, sizeof(key_s));
num_key = 0;
for(int i=0;i<n;i++)
{
scanf("%s", mp[i]);
for(int j=0;j<m;j++)
{
if(mp[i][j] == 'S')
sx = i, sy = j;
if(mp[i][j] == 'E')
ex = i, ey = j;
if(mp[i][j] == 'K')
{
key_s[i][j] = (1 << num_key);
num_key++;
}
}
}
int ans = bfs();
printf("%d\n", ans);
}
return 0;
}























 1809
1809

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








