HDU 5288 OO's sequence (2015多校第一场 二分查找）

OO’s Sequence

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 131072/131072 K (Java/Others)
Total Submission(s): 955    Accepted Submission(s): 358

Problem Description

OO has got a array A of size n ,defined a function f(l,r) represent the number of i (l<=i<=r) , that there's no j(l<=j<=r,j<>i) satisfy a _i mod a _j=0,now OO want to know

（）

 

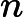
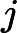
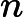
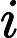
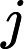
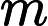
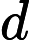
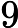
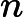
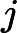
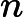
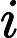
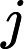
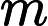
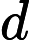
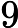
Input

There are multiple test cases. Please process till EOF.
In each test case: 
First line: an integer n(n<=10^5) indicating the size of array
Second line:contain n numbers a _i(0<a _i<=10000)

 

Output

For each tests: ouput a line contain a number ans.

 

Sample Input

  
  

   
   5
1 2 3 4 5
  
  

 

Sample Output

  
  

   
   23
  
  

 

Author

FZUACM

 

Source

2015 Multi-University Training Contest 1

解题思路：
预处理出所有数的因数并且保存每个数出现的位置，对于每个A[i]， 找最小的区间使得该区间内不包含A[i]的因数，通过向左向右进行两次二分查找来实现。

#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
#include <cmath>
#include <queue>
#include <stack>
#include <algorithm>
using namespace std;
const int MAXN = 100000 + 10;
const int MOD = 1e9 + 7;
vector<int>G[MAXN];
vector<int>p[MAXN];
vector<int>rp[MAXN];
vector<int>M[MAXN];
int N;
int A[MAXN];
int main()
{
    for(int i=1; i<=10000; i++)
    {
        for(int j=i; j<=10000; j+=i)
            G[j].push_back(i);
    }
    while(scanf("%d", &N)!=EOF)
    {
        for(int i=1;i<=N;i++) p[i].clear();
        for(int i=1;i<=N;i++) rp[i].clear();
        for(int i=1; i<=N; i++)
            scanf("%d", &A[i]);
        for(int i=1; i<=N; i++)
        {
            p[A[i]].push_back(i);
        }
        for(int i=N;i>=1;i--)
        {
            rp[A[i]].push_back(-i);
        }
        long long ans = 0;
        for(int i=1; i<=N; i++)
        {
            int L = -1, R = N + 1;
            for(int j=0; j<G[A[i]].size(); j++)
            {
                int x = G[A[i]][j];
                int r = upper_bound(p[x].begin(), p[x].end(), i) - p[x].begin();
                int l = upper_bound(rp[x].begin(), rp[x].end(), -i) - rp[x].begin();
                if(r >= p[x].size()) r = N  + 1;
                else r = p[x][r];
                //cout << x << ": " << l << ' '<< r << endl;
                if(l >= rp[x].size()) l = 0;
                else l = -(rp[x][l]);
                //cout << x << ": " << l << ' '<< r << endl;
                L = max(l, L);
                R = min(R, r);
            }
            if(R == 0) R = N + 1;
            if(L < 0) L = 0;
            //cout << L << ' ' << R << endl;
            ans = (ans + (long long)(i - L) * (long long)(R - i)) % MOD;
        }
        printf("%I64d\n", ans );
    }
    return 0;
}