1,课本教材习题5.18.
a,根据字母及空格出现的频率,可构造哈夫曼树,
(1)根据字母及空格出现的频率,可构造哈夫曼树,如下图:
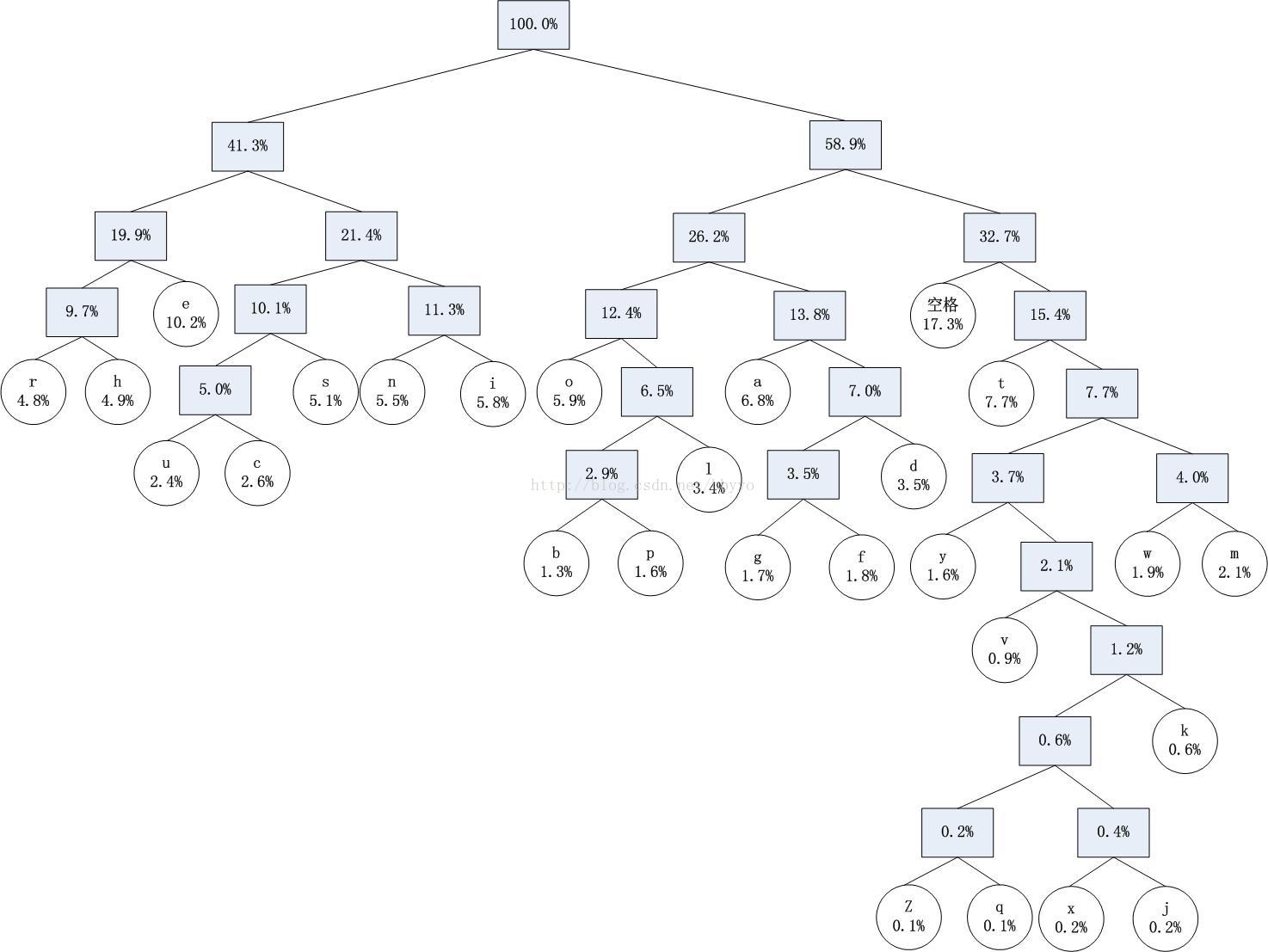
利用哈夫曼编码定义,可得出哈夫曼编码为:
z:1111011000
q:1111011001
x:1111011010
j: 1111011011
k:11110111
v:1111010
b:100100
p:100101
y:111100
g:101100
f:101101
w:111110
m:111111
u:01000
c:01001
l:10011
d:10111
r:0000
h:0001
s:0101
n:0110
i:0111
o:1000
a:1010
t:1110
e:001
空格:110
b,根据哈夫曼树可得出每个字母编码平均需要的位数为:(10*4+8+7+6*7+5*4+4*8+3*2)/27=5.7407
c,我认为熵的值比以上计算结果要大,因为每一个字母编码实际中是整数,而以上计算为小数,如果舍去小数部分,只取整数部分就偏小了,故应该偏大才行。
d,我不认为这就是英文文本压缩的下限,因为英文文本的复杂度还远远地比这个深,除了字母及其出现频率,还有英文词组,字母的前缀和后缀应该被考虑到的。










 本文详细探讨了使用哈夫曼编码进行文本压缩的方法,并对其效率进行了评估,同时指出了当前方法的局限性和改进方向,强调了在压缩过程中考虑英文词组、字母前缀和后缀的重要性。
本文详细探讨了使用哈夫曼编码进行文本压缩的方法,并对其效率进行了评估,同时指出了当前方法的局限性和改进方向,强调了在压缩过程中考虑英文词组、字母前缀和后缀的重要性。
















 1056
1056

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








