目录
字典树,又称前缀树或单词查找树,优点是最大限度的减少无谓的字符串比较,查询效率比哈希表高。Trie树的核心思想是空间换时间,利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。缺点是内存消耗很大。
trie树把要查找的关键词看作一个字符序列,并根据构成关键词字符的先后顺序构造用于检索的树结构,类似于查阅英语词典。
1.基本性质
A.根节点不包含字符,每条边代表一个字符;
B.从根节点到某一结点,路径上经过的字符连接起来,为该节点对应的字符串;
C.每个节点的所有子节点包含的字符都不相同。
2.字典树的构建
好比假设有b,abc,abd,bcd,abcd,efg,hii 这6个单词,我们构建的树就是如下图这样的。
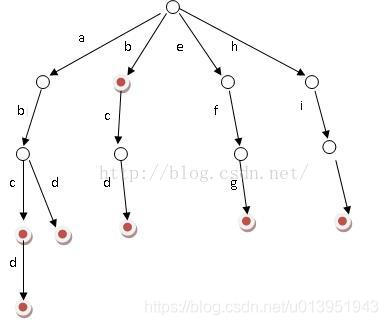
如上图所示,对于每一个节点,从根遍历到他的过程就是一个单词,如果这个节点被标记为红色,就表示这个单词存在,否则不存在。
那么,对于一个单词,我只要顺着他从根走到对应的节点,再看这个节点是否被标记为红色就可以知道它是否出现过了。把这个节点标记为红色,就相当于插入了这个单词。
3.代码实现(c++版)
myhead.h文件如下:
#pragma once
#include <iostream>
#include <cstdlib>
#include <vector>
#include <string>
#include <set>
#include <algorithm>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <cmath>
#include <climits>
主程序如下:
#include "stdafx.h"
#include "myhead.h"
class TrieNode // 字典树节点
{
private:
bool isEnd; // 标记是否是一个单词的结束
int index; // 单词序号
std::vector<TrieNode*> children; // 当前节点的子节点
public:
TrieNode() :index(-1), isEnd(false), children(26, nullptr) {}
~TrieNode() {
for (int i = 0; i < 26; ++i)
if (children[i] != nullptr) {
delete children[i];
children[i] = nullptr;
}
}
// 对外接口
int getIndex() { return index; }
void setIndex(int i) { index = i; }
bool isWordEnd() { return isEnd; }
void setWordEnd() { isEnd = true; }
// 插入一个字符到子节点
TrieNode* insertNode(const char c)
{
if (!('a' <= c && c <= 'z')) return nullptr;
auto id = c - 'a';
if (children[id] == nullptr) // 当前字符不存在
children[id] = new TrieNode();
return children[id];
}
// 在子节点中寻找一个字符
TrieNode* getNode(const char c)
{
if (!('a' <= c && c <= 'z')) return nullptr;
auto id = c - 'a';
return children[id];
}
};
class TrieTree {
private:
TrieNode * root;
public:
TrieTree() :root(new TrieNode()) {}
~TrieTree() { delete root; }
//插入一个单词及序号
void insert(std::string word, int index)
{
auto p = root;
for (auto i = 0; i < word.size(); ++i)
p = p->insertNode(word[i]);
p->setWordEnd();
p->setIndex(index);
}
// 查找一个字符串
TrieNode *getNode(std::string word)
{
auto p = root;
for (int i = 0; i < word.size(); ++i)
{
p = p->getNode(word[i]);
if (p == nullptr)
return nullptr;
}
return p;
}
// 查找一个单词并返回序号
bool search(std::string word, int &index)
{
auto p = getNode(word);
if (p)
{
index = p->getIndex();
return p->isWordEnd();
}
return false;
}
};
int main()
{
std::vector<std::string> vec{ "abc", "hello", "world", "ni", "hao" };
TrieTree *tree = new TrieTree();
for (int i = 0; i < vec.size(); ++i)
tree->insert(vec[i], i);
std::cout << "输入你想找的单词:" << std::endl;
std::string temp;
std::cin >> temp;
int index = -1;
if (tree->search(temp, index))
{
std::cout << "找到单词, 它在" << index << "位置" << std::endl;
}
system("pause");
return EXIT_SUCCESS;
}
4.通过字典树实现leetcode 336题
题目描述:
给定一组 互不相同 的单词, 找出所有不同 的索引对(i, j),使得列表中的两个单词, words[i] + words[j] ,可拼接成回文串。
示例 1:
输入:["abcd","dcba","lls","s","sssll"]
输出:[[0,1],[1,0],[3,2],[2,4]]
解释:可拼接成的回文串为 ["dcbaabcd","abcddcba","slls","llssssll"]
示例 2:
输入:["bat","tab","cat"]
输出:[[0,1],[1,0]]
解释:可拼接成的回文串为 ["battab","tabbat"]
思路:
如果字符串 S1 + S2 能构成一个回文串,把 S1 分成 S1_1 和 S1_2 两部分,可以有以下以下两种拼接情况:
①.S2 拼接在前,并且 S1_1 是回文串、 S1_2 是 S2 的逆序;
②.S2 拼接在后,并且 S1_2 是回文串、 S1_1 是 S2 的逆序;

或者可以这么理解,可以拼接成回文字符串的有以下四种情况:
1.s是回文字符串&&t是空串 || t是回文字符串 && s是空串 ==> s+t, t+s都是回文字符串
2.t是s的逆序==>s+t, t+s都是回文字符串
3.s可以分成s1, s2, st s1 + s2 == s && s1 是回文字符串 && s2是t的逆序 ==> t+s是回文字符串
4.s可以分成s1, s2, st s1+s2 == s && s1 是t的逆序 && s2是回文字符串 ==> s+t是回文字符串
代码如下:
//字典树节点
class TrieNode
{
private:
bool isEnd;//单词结束标记
int index;//单词序号
vector<TrieNode*> children;//子节点
public:
//构造
TrieNode():index(-1),isEnd(false),children(26,nullptr){}
//析构
~TrieNode()
{
for(int i = 0;i < 26;i++)
{
if( children[i])
{
delete children[i];
children[i] = nullptr;
}
}
}
//对外接口
int getIndex() { return index;}
void setIndex( int i) { index = i;}
bool isWordEnd() { return isEnd;}
void SetEnd(){ isEnd = true ;}
//插入一个字符到子节点
TrieNode * insertNode(char c)
{
if( !( 'a' <= c <= 'z')) return nullptr;
int id = c-'a';
if( children[id] == nullptr)
{
children[id] = new TrieNode();
}
return children[id];
}
//在子节点中查找一个字符
TrieNode * getNode(char c)
{
if( !( 'a' <= c <= 'z')) return nullptr;
int id = c-'a';
return children[id] ;
}
};
//字典树
class Trie
{
private:
TrieNode * root;//根节点
public:
Trie():root(new TrieNode()){}
~Trie() { delete root;}
//插入一个单词及序号
void insert( string word,int index)
{
TrieNode * p = root;
for( int i = 0;i<word.size();i++)
{
p = p->insertNode(word[i]);
}
p->SetEnd();
p->setIndex(index);
}
//查找一个字符串
TrieNode *getNode(string word)
{
TrieNode * p = root;
for(int i = 0;i < word.size();i++ )
{
p = p->getNode(word[i]) ;
if( p == NULL ) return NULL;
}
return p;
}
//查找一个单词,返回序号
bool search(string word,int &index)
{
TrieNode * p = getNode(word);
if( p )
{
index = p->getIndex();
return p->isWordEnd();
}
return false;
}
};
class Solution {
public:
vector<vector<int>> palindromePairs(vector<string>& words) {
vector<vector<int>> res;
//构建字典树
Trie * trieTree = new Trie();
for(int i = 0;i < words.size();i++)
{
trieTree->insert(words[i],i);
}
for(int i = 0;i < words.size();i++)
{
for(int j = 0;j < words[i].size();j++ )
{
bool flag = check(words[i],0,j);
if(flag)//前半截是回文
{
string temp = words[i].substr(j+1);
reverse(temp.begin(),temp.end());
int index = -1;
if( trieTree->search(temp,index) )
{
if( i != index )
{
res.push_back({index,i});
if( temp == "")
{
res.push_back({i,index});
}
}
}
}
flag = check(words[i],j+1,words[i].size()-1);
if(flag)//后半截是回文
{
string temp = words[i].substr(0,j+1);
reverse(temp.begin(),temp.end());
int index = -1;
if( trieTree->search(temp,index) )
{
if( i != index )
res.push_back({i,index});
}
}
}
}
return res;
}
bool check(string &vec,int left,int right)
{
int i = left;
int j = right;
while(i <= j)
{
if( vec[i] != vec[j]) return false;
i++;
j--;
}
return true;
}
};
参考文献:
- https://blog.youkuaiyun.com/sunhuaqiang1/article/details/52463257?utm_medium=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param&depth_1-utm_source=distribute.pc_relevant.none-task-blog-BlogCommendFromMachineLearnPai2-1.channel_param
- https://leetcode-cn.com/problems/palindrome-pairs/solution/c-zi-dian-shu-zhu-shi-xiang-xi-by-li-zhi-chao-4/

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








