1.2 线性表——链表

最新推荐文章于 2025-01-09 20:50:02 发布
最新推荐文章于 2025-01-09 20:50:02 发布
阅读量311 收藏
点赞数
分类专栏： 阿导算法学习之路 文章标签： 线性表 链表 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/u013930425/article/details/103180019
版权

什么是链表

链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。

列表（也成为顺序表）和链表都是线性表，那他们有什么区别呢？从结构上来说，列表底层是通过数组来存储数据，需要申请空间，然后按照次序逐一存储，数据之间紧密贴合，数据之间联系是索引；链表每个节点只保留存储元素和下个节点指针，所以什么时候存数据就什么时候申请空间，数据之间联系是每个节点携带的指针。

  • 空间利用率

从结构上就能看出列表的空间利用率比链表高，因为链表在存储数据的时候每次都只申请一个节点的空间，且空间的位置是随机的，这样便会产生很多空间碎片，一定程度上造成空间浪费；另外链表每个节点都至少带一个指针，所以链表申请空间的利用率也比列表低。

  • 时间复杂度

因为列表底层是由数组实现的，访问元素，直接通过索引就能够获取元素，时间复杂度为 O(1)，而链表需要遍历节点到指定位置，所以链表访问元素的时间复杂度为 O(n)。但是在删除和插入两种操作中，数组需要因为，因此时间复杂度为 O(n),而链表直接操作某个节点即可，因此时复杂度为O(1)，因此，如何使用列表和链表可根据具体的业务场景进行选择。

  1. 若是业务场景查询操作比较多，但修改删除操作比较少，建议使用列表

  2. 若是业务场景修改删除操作比较多，但查询操作比较少，建议使用链表

最后阿导从其它地方找到一个表格进行总结，如下

比对项链表列表（数组）
内存占用不需要连续的内存空间需要连续的内存空间
大小可变可动态变化数组大小固定，不能动态扩展
增删较快，只需要修改前一个元素的指针即可较慢，需要移动修改元素之后的所有元素
查询较慢，只能遍历查找较快，直接通过下标索引直接访问
访问方式必须是顺序访问，不能随机访问可随机访问其中的元素
空间使用可以随意扩大不能随意扩大

说完链表和列表的区别，在链表中常见的有单向链表，双向链表，下面逐一分析这三种链表。

单向链表

结构


    private class Node<E> {
        /**
         * 元素
         */
        private E e;
        /**
         * 下一个节点
         */
        private Node<E> next;

    }

单链表数据结构

单向链表结构体中包含存储数据区域的 e,和指向下一个节点的指针 next。

操作

  • 新增元素：public boolean add(E e)

单链表新增元素

新增元素一般是将新增的元素添加到链表的尾部，一般这里面可以通过 size 来遍历至链表的最后一个元素，我这边根据判断每个元素下一个节点是否为空来判断是否是最后一个元素，这里面需要区别对待的是头节点，因为在操作类需要保留头节点信息。最后统计链表大小属性 size 加一。

  • 插入元素：public boolean add(int index, E e)

单向链表插入元素

插入元素，首先是需要判断插入的位置是否合法，然后找出插入的位置，插入元素需要注意的是后续指针区域的变化，这也是和列表中数组移位不相同的一点。最后统计链表大小属性 size 加一。

  • 查询第一个匹配到的位置：public int indexOf(E e)

链表中访问元素必须是顺序访问，从头节点依次遍历，直到查询到目标元素或最后一个节点结束。

  • 移除某个位置的节点：public E remove(int index)

单向链表删除元素

移除某个位置的元素，第一步仍然需要判断移除的位置是否合法，然后找寻到移除位置，这里移除也不需要向数组那样移位，只需要处理移除的位置前后节点即可，这里需要注意的是头节点没有前驱节点。最后记得将统计链表大小的 size 减一。

  • 移除链表上某个元素：public E remove(E e)

这里实现方式也比较多，第一种是通过遍历，进行匹配然后进行删除指定的位置信息，我这里的做法其实不建议使用，只是为了偷懒，先查询到位置，再移除该位置的元素。

  • 修改指定位置的数据区域： public void set(int index, E e)

判断修改位置的合法性，然后找到位置直接修改元素即可。

  • 判断元素是否存在： public boolean contains(E e)

这里可借助 indexOf 方法进行判断即可。

  • 判断是否为空：public boolean isEmpty()

直接根据 size 是否为零进行判断。

  • 获取指定位置的数据：public E getData(int index)

判断位置合法性，然后依次遍历到该位置取出数据区域的数据即可。

  • 获取链表大小：public int size()

直接返回统计链表大小属性 size。

  • 转换成数组：public Object[] toArray()

通过遍历赋值到数组并返回。

  • 重写 toString 方法：public String toString()

通过连接符进行形象表示链式结构。

  • 清空链表：public void clear()

将头节点置为空，统计链表大小的属性 size 置为 0。

示例


package com.dao.datastructure.list;

/**
 * 链表
 *
 * @author 阿导
 * @CopyRight 万物皆导
 * @Created 2019-11-18 19:28:00
 */
public class DaoLinkedList<E> {
    /**
     * 节点内部类
     *
     * @author 阿导
     * @time
     * @copyRight 万物皆导
     */
    private class Node<E> {
        /**
         * 元素
         */
        private E e;
        /**
         * 下一个节点
         */
        private Node<E> next;

        private Node() {
            this(null);
        }

        private Node(E e) {
            this(e, null);
        }

        private Node(E e, Node<E> next) {
            this.e = e;
            this.next = next;
        }

    }

    /**
     * 头节点
     */
    private Node head;
    /**
     * 节点数目
     */
    private int size;

    /**
     * 构造方法
     *
     * @return
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public DaoLinkedList() {
        this.head = null;
        this.size = 0;
    }

    /**
     * 添加元素
     *
     * @param e
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean add(E e) {
        // 新节点
        Node<E> newNode = new Node(e);
        // 找到链表最尾部，然后插入结果即可（头节点比较特殊）
        if (this.size == 0 && this.head == null) {
            this.head = newNode;
        } else {
            // 临时遍历获取当前头节点
            Node<E> next = this.head;
            // 遍历直到尾节点
            while (next.next != null) {
                next = next.next;
            }
            // 将尾节点的下一个节点指向新节点
            next.next = newNode;
        }
        // 节点大小加一
        this.size++;
        // 操作成功
        return true;
    }

    /**
     * 指定位置插入节点
     *
     * @param index
     * @param e
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean add(int index, E e) {
        // 判断插入的位置是否合法
        this.indexOutOfBoundsException(index);
        // 记录位置
        int pox = 0;
        // 获取头节点
        Node<E> next = this.head;
        // 记录上一个节点
        Node<E> cur = null;
        // 找到插入位置
        while (pox++ < index) {
            // 当前节点保存
            cur = next;
            // 下一节点
            next = next.next;
        }
        //若是此种情况，则是头节点
        if (cur == null) {
            // 新节点的下一个节点是头节点
            Node<E> newNode = new Node(e, this.head);
            // 将头节点指向新节点
            this.head = newNode;
        } else {
            // 新节点的下一个节点当前节点的下一个节点
            Node<E> newNode = new Node(e, next);
            // 当前节点指向新节点
            cur.next = newNode;
        }
        // 节点大小加一
        this.size++;
        // 操作成功
        return true;
    }

    /**
     * 查询第一个匹配到的位置
     *
     * @return int
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public int indexOf(E e) {
        // 记录位置
        int pox = 0;
        // 获取头节点
        Node<E> cur = this.head;
        // 遍历节点
        while (cur != null) {
            // 若查询到节点，则返回位置
            if ((cur.e == null && e == null) || e != null && e.equals(cur.e)) {
                return pox;
            }
            // 下个节点走起
            cur = cur.next;
            pox++;
        }
        // 表示未找到
        return -1;
    }

    /**
     * 移除某个位置的节点
     *
     * @param index
     * @return E
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public E remove(int index) {
        // 判断插入的位置是否合法
        this.indexOutOfBoundsException(index);
        // 记录位置
        int pox = 0;
        // 记录上一个节点
        Node<E> cur = null;
        // 获取头节点
        Node<E> next = this.head;
        // 找到插入位置
        while (pox++ < index) {
            // 当前节点保存
            cur = next;
            // 下一节点
            next = next.next;
        }
        // 保留删除的节点
        E e = (E) next.e;
        if (cur == null) {
            // 若是删除头节点,直接将头节点指向头节点的下一个节点即可
            this.head = this.head.next;
        } else {
            // 当前节点下一个节点指向下一个节点的下一个节点
            cur.next = next.next;
        }
        // 节点大小减一
        this.size--;

        return e;
    }

    /**
     * 移除链表上某个元素
     *
     * @param e
     * @return E
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public E remove(E e) {
        int index = this.indexOf(e);
        // 未查询到不做任何处理，直接返回
        if (index == -1) {
            return e;
        }
        // 移除元素
        remove(index);
        // 直到所有的元素都删除
        return remove(e);
    }
    /**
     * 修改内容
     *
     * @author 阿导
     * @time 2019/11/20 :00
     * @param index
     * @param e
     * @return void
     */
    public void set(int index, E e) {
        // 判断插入的位置是否合法
        this.indexOutOfBoundsException(index);
        // 记录位置
        int pox = 0;
        Node<E> cur = this.head;
        // 查找指定位置
        while (pox++ < index) {
            cur = cur.next;
        }
        // 替换元素
        cur.e = e;
    }
    /**
     * 重写 toString
     *
     * @author 阿导
     * @time 2019/11/20 :00
     * @return java.lang.String
     */
    @Override
    public String toString() {
        // 声明结果
        StringBuilder sb = new StringBuilder();
        // 当前节点
        Node<E> cur = this.head;
        // 遍历节点
        while (cur != null) {
            // 获取当前节点元素
            sb.append(cur.e);
            // 是否需要连接符号
            if (cur.next != null) {
                sb.append("->");
            }
            // 指针指向下一个节点
            cur = cur.next;
        }
        // 返回结果
        return sb.toString();
    }

    /**
     * 判断元素是否存在
     *
     * @param e
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean contains(E e) {
        return this.indexOf(e) > -1;
    }

    /**
     * 判断是否为空
     *
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean isEmpty() {
        return this.size == 0;
    }

    /**
     * 查找指定位置的数据
     *
     * @param index
     * @return E
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public E getData(int index) {
        this.indexOutOfBoundsException(index);
        // 记录位置
        int pox = 0;
        Node<E> cur = this.head;
        // 查找指定位置
        while (pox++ < index) {
            cur = cur.next;
        }

        return cur.e;
    }

    /**
     * 转换成数组
     *
     * @return E[]
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public Object[] toArray() {
        // 存储结果
        Object[] obj = new Object[this.size];
        // 获取头节点
        Node<E> cur = this.head;
        // 记录位置
        int pox = 0;
        // 遍历节点
        while (cur != null) {
            // 获取元素
            obj[pox++] = cur.e;
            // 指向下一个节点
            cur = cur.next;
        }
        // 返回结果
        return obj;
    }

    /**
     * 获取链表大小
     *
     * @return int
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public int size() {
        return this.size;
    }

    /** 
     * 清空链表
     *
     * @author 阿导
     * @time 2019/11/20 :00
     * @return void
     */
    public void clear(){
        this.head = null;
        this.size=0;
    }
    
    /**
     * 判断是否越界
     *
     * @param index
     * @return void
     * @author 阿导
     * @time 2019/11/19 :00
     */
    private void indexOutOfBoundsException(int index) {
        if (index >= this.size || index < 0) {
            throw new ArrayIndexOutOfBoundsException("位置越界！！！");
        }
    }


}

双向链表

结构


  private class Node<E> {
        /**
         * 节点元素
         */
        private E e;
        /**
         * 上一个节点
         */
        private Node<E> pre;
        /**
         * 下一个节点
         */
        private Node<E> next;
        
   }

双向链表最基本的结构有三个，分别是存储数据的 e,指向上一个节点 pre,以及指向下一个节点的 next。

双向链表数据结构

操作

  • 新增元素：public boolean add(E e)

双向链表新增元素

双向链表相比较单向链表能更快的添加新的元素，因为双向链表会存储尾节点，所以直接替换尾节点即可，这里主要注意的是第一个节点进来如何处理，新节点前驱节点和后续节点怎么处理。最后统计链表大小属性 size 加一。

  • 插入元素：public boolean add(int index, E e)

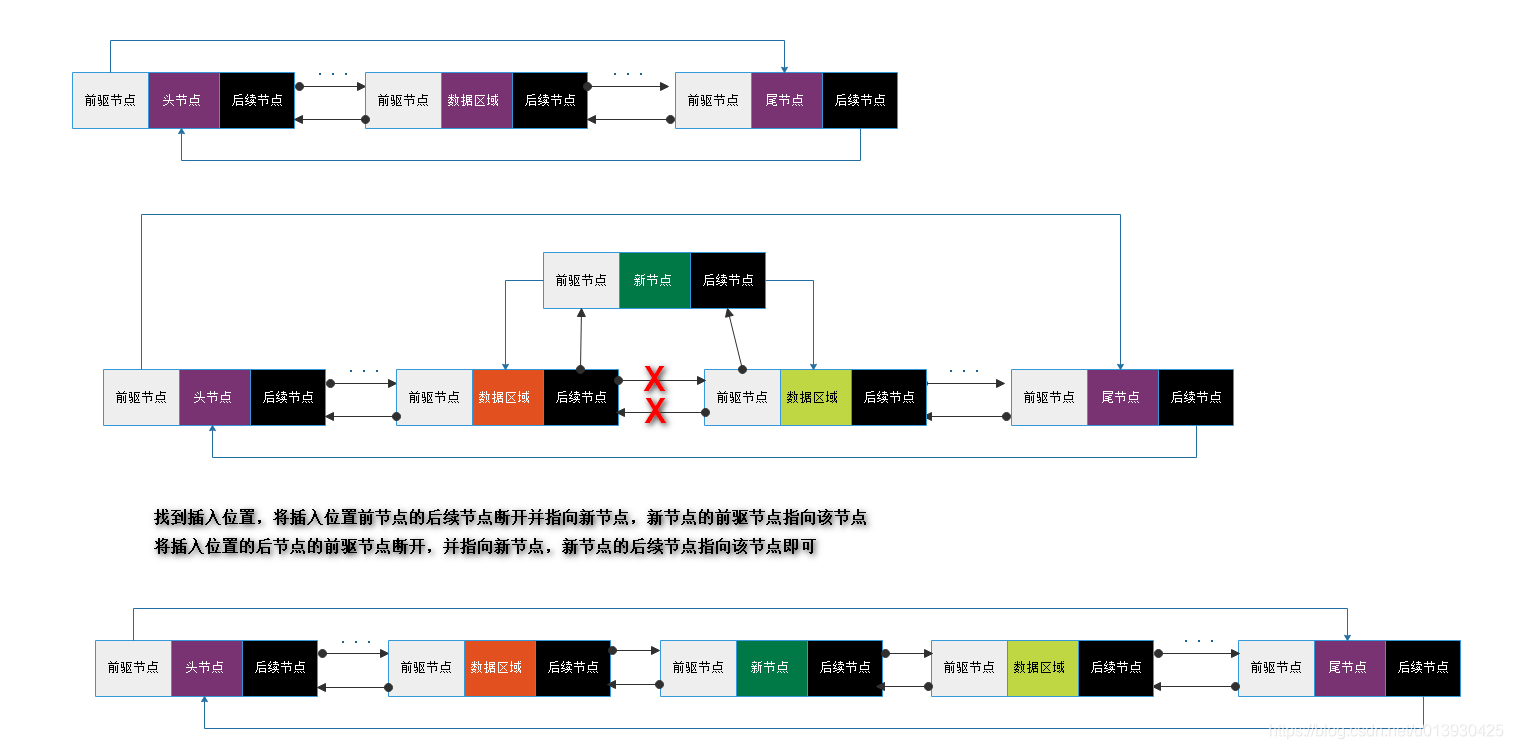
双向链表插入元素

插入元素，首先是需要判断插入的位置是否合法，然后找出插入的位置，这里相对单向节点可以根据插入位置离头尾节点距离一定程度上减少遍历次数，这里依旧注意的是插入头节点的情况，最后要处理好新节点和旧节点的指针指向。最后统计链表大小属性 size 加一。

  • 查询第一个匹配到的位置：public int indexOf(E e)

可以同时从头节点和尾节点，双向查找，谁最先查到相同的元素，先返回谁的序列位置

  • 移除某个位置的节点：public E remove(int index)

双向链表移除元素

移除某个位置的元素，第一步仍然需要判断移除的位置是否合法，不过这里需要注意的是移除的元素是否是最后一个元素，另外是否是头节点或者尾节点，最后需要处理好每个节点的指针指向。最后记得将统计链表大小的 size 减一。

  • 移除链表上某个元素：public E remove(E e)

这里实现和单向链表类似。

  • 修改指定位置的数据区域： public void set(int index, E e)

判断修改位置的合法性，然后找到位置直接修改元素即可。

  • 判断元素是否存在： public boolean contains(E e)

这里可借助 indexOf 方法进行判断即可。

  • 判断是否为空：public boolean isEmpty()

直接根据 size 是否为零进行判断。

  • 获取指定位置的数据：public E getData(int index)

判断位置合法性，然后找到位置取出数据区域的数据即可。

  • 获取链表大小：public int size()

直接返回统计链表大小属性 size。

  • 转换成数组：public Object[] toArray()

通过遍历赋值到数组并返回。

  • 重写 toString 方法：public String toString()

通过连接符进行形象表示链式结构。

  • 清空链表：public void clear()

将头尾节点置为空，统计链表大小的属性 size 置为 0。

示例


package com.dao.datastructure.list;

/**
 * 双向链表
 *
 * @author 阿导
 * @CopyRight 万物皆导
 * @Created 2019-11-19 15:27:00
 */
public class DaoDoubleLinkedList<E> {

    private class Node<E> {
        /**
         * 节点元素
         */
        private E e;
        /**
         * 上一个节点
         */
        private Node<E> pre;
        /**
         * 下一个节点
         */
        private Node<E> next;


        public Node() {
        }

        public Node(E e) {
            this.e = e;
        }

        public Node(E e, Node<E> pre, Node<E> next) {
            this.e = e;
            this.pre = pre;
            this.next = next;
        }
    }

    /**
     * 节点
     */
    private Node<E> head;
    /**
     * 尾节点
     */
    private Node<E> foot;
    /**
     * 大小
     */
    private int size;


    /**
     * 构造方法
     *
     * @return
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public DaoDoubleLinkedList() {
        this.head = null;
        this.foot = null;
        this.size = 0;
    }

    /**
     * 添加元素
     *
     * @param e
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean add(E e) {

        // 找到链表最尾部，然后插入结果即可（头节点比较特殊）
        if (this.size == 0 && this.head == null && this.foot == null) {
            // 新节点
            Node<E> newNode = new Node(e);
            // 头尾节点都是本身
            this.head = newNode;
            this.foot = newNode;
            this.head.next = this.foot;
            this.head.pre = this.foot;
        } else {
            // 新节点，前驱指针指向头部，后续指针指向尾节点
            Node<E> newNode = new Node(e, this.foot, this.head);
            // 尾节点的后续指针指向新节点
            this.foot.next = newNode;
            // 头节点的前驱指针指向新节点
            this.head.pre = newNode;
            // 新节点为尾节点
            this.foot = newNode;
        }
        // 节点大小加一
        this.size++;
        // 操作成功
        return true;
    }

    /**
     * 指定位置插入节点
     *
     * @param index
     * @param e
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean add(int index, E e) {
        // 判断插入的位置是否合法
        this.indexOutOfBoundsException(index);
        // 记录位置
        int pox = 0;
        // 获取最多访问次数
        int n = this.size/ 2;
        // 获取头节点
        Node<E> next = this.head;
        // 记录上一个节点
        Node<E> cur = this.foot;
        // 若是离头节点比较近
        if (index < n) {
            while (pox++ < index) {
                // 当前节点保存
                cur = next;
                // 下一节点
                next = next.next;
            }
        } else {
            while (pox++ < this.size - index) {
                // 下一节点
                next = cur;
                // 当前节点保存
                cur = cur.pre;
            }
        }
        //若是此种情况，则是头节点
        if (cur == null) {
            // 若插入的是头节点
            Node<E> newNode = new Node(e, this.foot, this.head);
            // 当头节点前驱指针指向新节点
            this.head.pre = newNode;
            // 尾节点的后续指针指向新节点
            this.foot.next = newNode;
            // 新节点作为头节点
            this.head = newNode;
        } else {
            // 新节点，下一个节点指向 next，上一个节点指向 cur
            Node<E> newNode = new Node(e, cur, next);
            // 当前节点后续指针指向新节点
            cur.next = newNode;
            // 下一个节点前驱指针指向新节点
            next.pre = newNode;
        }
        // 节点大小加一
        this.size++;
        // 操作成功
        return true;
    }

    /**
     * 查询离头或根节点最近的节点
     *
     * @return int
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public int indexOf(E e) {
        // 记录位置
        int pox = 0;
        // 获取头节点
        Node<E> curNext = this.head;
        Node<E> curPre = this.foot;
        // 获取最多访问次数
        int n = (this.size + 1) / 2;
        // 遍历节点
        while (pox < n) {
            // 若查询到节点，则返回位置
            if ((curNext.e == null && e == null) || e != null && e.equals(curNext.e)) {
                return pox;
            }
            if ((curPre.e == null && e == null) || e != null && e.equals(curPre.e)) {
                return this.size - pox - 1;
            }
            // 下个节点走起
            curNext = curNext.next;
            curPre = curPre.pre;
            pox++;
        }
        // 表示未找到
        return -1;
    }

    /**
     * 移除某个位置的节点
     *
     * @param index
     * @return E
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public E remove(int index) {
        // 判断插入的位置是否合法
        this.indexOutOfBoundsException(index);

        // 获取最多访问次数
        int n = this.size / 2;
        // 记录位置
        int pox = 0;
        // 记录上一个节点
        Node<E> curPre = this.foot;
        // 获取头节点
        Node<E> curNext = this.head;
        // 若是离头节点比较近
        if (index < n) {
            while (pox++ < index) {
                curPre = curNext;
                curNext = curNext.next;
            }
        } else {
            while (pox++ < this.size - index) {
                curNext = curPre;
                curPre = curPre.pre;
            }
        }

        // 保留删除的节点
        E e = curNext.e;
        // 若是头节点
        if (curNext.equals(this.head)) {
            // 若是删除头节点,直接将头节点指向头节点的下一个节点即可
            if (this.size == 1) {
                this.head = null;
                this.foot = null;
            } else {
                this.head = this.head.next;
                this.head.pre = this.foot;
                this.foot.next = this.head;
            }
        } else if (curNext.equals(this.foot)) {
            e = curPre.e;
            // 若是尾节点
            this.foot = this.foot.pre;
            this.foot.next = this.head;
            this.head.pre = this.foot;
        } else {
            curPre.next = curNext.next;
            curNext.next.pre = curPre;
        }
        // 节点大小减一
        this.size--;

        return e;
    }

    /**
     * 移除链表上某个元素
     *
     * @param e
     * @return E
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public E remove(E e) {
        int index = this.indexOf(e);
        // 未查询到不做任何处理，直接返回
        if (index == -1) {
            return e;
        }
        // 移除元素
        remove(index);
        // 直到所有的元素都删除
        return remove(e);
    }

    /**
     * 修改内容
     *
     * @param index
     * @param e
     * @return void
     * @author 阿导
     * @time 2019/11/20 :00
     */
    public void set(int index, E e) {
        // 判断插入的位置是否合法
        this.indexOutOfBoundsException(index);
        // 获取最多访问次数
        int n = (this.size + 1) / 2;
        // 记录位置
        int pox = 0;
        Node<E> cur = this.head;
        // 若是离头节点比较近
        if (index < n) {
            while (pox++ < index) {
                cur = cur.next;
            }
        } else {
            cur = this.foot;
            while (pox++ < this.size - index - 1) {
                cur = cur.pre;
            }
        }
        // 替换元素
        cur.e = e;
    }

    /**
     * 重写 toString
     *
     * @return java.lang.String
     * @author 阿导
     * @time 2019/11/20 :00
     */
    @Override
    public String toString() {
        // 声明结果
        StringBuilder sb = new StringBuilder();
        // 当前节点
        Node<E> cur = this.head;
        // 遍历节点
        while (!cur.equals(this.foot)) {
            // 获取当前节点元素
            sb.append(cur.e);
            // 是否需要连接符号
            sb.append("->");
            // 指针指向下一个节点
            cur = cur.next;
        }
        sb.append(this.foot.e);
        // 返回结果
        return sb.toString();
    }

    /**
     * 判断元素是否存在
     *
     * @param e
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean contains(E e) {
        return this.indexOf(e) > -1;
    }

    /**
     * 判断是否为空
     *
     * @return boolean
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public boolean isEmpty() {
        return this.size == 0;
    }

    /**
     * 查找指定位置的数据
     *
     * @param index
     * @return E
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public E getData(int index) {
        this.indexOutOfBoundsException(index);
        // 记录位置
        int pox = 0;
        Node<E> cur = this.head;
        // 查找指定位置
        while (pox++ < index) {
            cur = cur.next;
        }

        return cur.e;
    }

    /**
     * 转换成数组
     *
     * @return E[]
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public Object[] toArray() {
        // 存储结果
        Object[] obj = new Object[this.size];
        // 获取头节点
        Node<E> cur = this.head;
        // 记录位置
        int pox = 0;
        // 遍历节点
        while (cur != null) {
            // 获取元素
            obj[pox++] = cur.e;
            // 指向下一个节点
            cur = cur.next;
        }
        // 返回结果
        return obj;
    }

    /**
     * 获取链表大小
     *
     * @return int
     * @author 阿导
     * @time 2019/11/19 :00
     */
    public int size() {
        return this.size;
    }
    /**
     * 清空链表
     *
     * @author 阿导
     * @time 2019/11/20 :00
     * @return void
     */
    public void clear(){
        this.head = null;
        this.foot = null;
        this.size = 0;
    }
    /**
     * 判断是否越界
     *
     * @param index
     * @return void
     * @author 阿导
     * @time 2019/11/19 :00
     */
    private void indexOutOfBoundsException(int index) {
        if (index >= this.size || index < 0) {
            throw new ArrayIndexOutOfBoundsException("位置越界！！！");
        }
    }

}

结束语

作为一个java 从业者，我们需要了解的是 LinkedList，查看源码即可知道，节点的定义和我这里面说的双向链表一致，所以它也是一个双向链表，一般面试官都喜欢问的话题就是拿它和顺序表进行对比，也就是 ArrayList（通过数组实现），他们都实现了 List 和 Collection 接口，具体类图如下所示，他们的区别在本文开篇基本已阐述，此处不再赘述。

类图

不知各位看官对链表是否有一定的了解，如有疑问，欢迎留言，如有不当之处，请多多包涵和指教！

线性表-链表
RenPeng_Ben的博客
08-01 563
链表 概论 wikipedia:链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是并不会按线性的顺序存储数据，而是在每一个节点里存到下一个节点的指针(Pointer)。由于不必须按顺序存储，链表在插入的时候可以达到O(1)的复杂度，比另一种线性表顺序表快得多，但是查找一个节点或者访问特定编号的节点则需要O(n)的时间，而顺序表相应的时间复杂度分别是O(logn)和O(1)。 链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数
线性表——链表ChainList的实现 C++
净无邪博客
03-07 2266
本文主要总结常用的数据结构——线性表之链式描述，实现其基本的增删查改功能，不涉及完整功能，目的是为了熟悉常用数据结构属性和代码实现底层原理。 顺序表结构有以下缺点： 插入或删除节点时，需要移动大量数据 如果表很大，有时难以分配连续存储空间，导致内存分配失败而无法存储 而链表内存空间却可以不是连续的，所以链表恰好解决了顺序表只能申请连续存储空间的缺点。那么，链表是什么呢？接下来让我们学习一下什么是链表？ 一、线性表——链式描述ChainList 1.1链表定义（链表数据结构的创建和调用（C++）） 链表
数据结构思维导图——线性表（最全）
m0_61105833的博客
09-13 1245
数据结构线性表思维导图
28、线性表
YGingko的专栏
04-29 458
应用程序中数据主要有四种基本的逻辑结构:
链表和list
chen_zan_yu_的博客
05-02 651
STL的 list ： 双向链表。它的内存空间不必连续，通过指针来进行数据的访问， 高效率地在任意地方删除和插入，插入和删除操作是常数时间。 ist和vector的优缺点正好相反，它们的应用场景不同： （1）vector：插入和删除操作少，随机访问元素频繁； （2）list：插入和删除频繁，随机访问较少。 例题： hdu 1276 士兵队列训练问题 一队士兵报数：从头开始1至2报数，...
链表列表
文龙的博客
04-12 3273
一、链表列表在存储方式上和数组列表的不同   链表列表的存储空间不连续。更有效利用了碎片化的存储空间。    二、什么是链表列表   链表列表由节点组成，每个节点上有存储的数据和下一个节点的地址，最后一个节点的指向下一个节点为null 三、定义链表列表   1.定义一个节点类，有数据和下一个节点两个属性 public class Node { private E data;
【数据结构】受限制的线性表——队列
HD_13的博客
03-20 2726
上一章我们讲了一种特殊的线性表只能在表尾进行插入和删除操作，接下来我们讲一个和栈很相似的数据结构，它也是一种特殊且所限制的线性表，它是只能在表头删除操作在表尾进行插入操作。
线性表——栈Stack的实现 C++
净无邪博客
03-12 1960
栈和队列是应用最多的数据结构之二，有数组实现和链表实现两种方式。当需要对容器做出限制，只允许一边插入和取出数据时，则需要用到栈。下面将总结数组实现的栈和阐述其原理。 一、线性表——栈Stack 1.1栈Stack定义 栈是一种特殊的线性表，其插入（也称为入栈或压栈）和删除（也称为弹出或出栈）操作都在表的同一端进行；该插入和删除的端口称为栈顶（top），另一端称为栈底（bottom）。 1.2栈的基本运算 1.2.1基本运算 (1) 初始化（构造一个空的栈） (2) 计算栈长度（栈中节点个数） (3) 插入节
第一章#1.2线性表的链式表示和实现
qq_54256430的博客
07-24 1422
###链式存储结构### 用任意物理位置存储，存储单元可能恰好连续，但逻辑顺序和物理顺序就不一定相同了。 在存储这一个元素的值还要存储下一个元素的地址。一个节点分成两个部分（数据域，指针域） 节点：数据元素的存储映像。数据域＋指针域。 链表：n个结点由指针链连接在一起。它是线性表的链式存储映像。 ※链表类型： 单链表：节点只有一个指针域的链表，称为单链表或线性链表。 双链表：结点有两个指针域的链表，一个用来存储上一结点地址，一个用存储下一结点的地址，还有一个数据域。 循环...
线性表的链式存储结构——链表及其操作(创建,查找,插入,输出,删除)
热门推荐
striver的博客
03-13 1万+
文章目录1.单链表的建立1.1头插法1.2尾插法2.链表基本操作 1.单链表的建立 1.1头插法 1)从一个空表开始，创建一个头结点。 2)依次读取数组a中的元素，生成新节点。 3)将新节点插入到当前链表的表头上，直到结束为止，插入过程如下图所示。 typedef struct LNode { int data; struct LNode *next;//存储后继节点位置的指针域，用next表示 }LinkNode; 头插法代码如下，由数组元素a创建单链表L void CreatListF(Lin
链表与列表的区别
最新发布
C6666888的博客
01-09 430
选择LinkedList还是ArrayList取决于具体的应用需求。理解这两种数据结构的工作原理及其各自的优缺点，可以帮助开发者根据实际情况做出最佳决策。此外，值得注意的是，两者都不是线程安全的实现；如果需要在线程并发环境中使用，必须采取额外措施确保同。
列表与链表
weixin_30267697的博客
10-06 604
列表 关于列表的存储： 　　列表开辟的内存空间是一块连续的内存，把这个内存等分成几份(单位是字节)，他是连续存储的。 　　如果一个列表长度已满，再append添加元素的话，会在内存中重新开辟一个2倍的内存空间以存储新元素，原列表内存会被清除。 链表------->列表相对应的数据结构 　　链表是一种线性数据结构（与树形结构相对），不是进行连续存储的。 　　链表中每一个元素都是一个对象...
列表与链表区别和联系
2303_76350311的博客
03-19 434
例如，如果需要频繁访问元素，列表可能是更好的选择；- **列表**：插入或删除元素时，可能需要移动大量元素以保持连续的内存空间，因此在非尾部插入或删除元素时，操作的时间复杂度为O(n)。- **链表**：插入或删除元素时，只需改变相应节点的指针，时间复杂度为O(1)（假设已经知道插入或删除位置的前一个节点）。- **链表**：不支持随机访问，要访问特定位置的元素需要从头开始遍历，时间复杂度为O(n)。1. **线性结构**：无论是列表还是链表，它们都是线性数据结构，元素之间是一对一的前后关系。
天生我才必有用——浅析Python列表与链表
the best messi的博客
03-26 1675
前言 之前写了一篇《没有指针，Python如何实现链表、二叉树这些数据结构》然后有大佬觉得我那里面讲的是列表，不是链表。当时我也很疑惑，因为我也不太确定列表和链表到底有什么区别，说实话，列表确实比较好用，因为是Python已经封装好了的，方法种类多样，更加的实用。但是这难道就意味着链表这一数据结构没有丝毫的用处嘛？当然不是，只是可能你还没有到非用他不可的地步罢了。 链表详解 链表的底层实现机制 翻...
python 列表和链表的区别
yake1965
07-11 5766
python 列表和链表的区别 Python中的list python中的list并不是我们传统意义上的列表 传统列表——通常也叫作链表(linked list)是由一系列节点来实现的，其中每个节点都持有一个指向下一节点的引用 简单实现起来应该就像下面那样： class Node: def init(self, value, next=None): self.value = value self.next = next 接下来，我们就可以将所有的节点构造成一个列表了： L = Node(“a”, No
数据结构之链表
weixin_30291791的博客
09-19 235
一、定义 链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。 链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。 每个结点包括两个部分： 1、存储数据元素的数据域， 2、下一个结点地址的指针域。 相比于线性表顺序结构，操作复杂。由于不必须按顺序存储，链表在插入的时候可以达到O...
C++ 单链表基本操作分析与实现
tomcat_kk的博客
12-05 4219
链表 　　链表是一种物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。链表由一系列结点（链表中每一个元素称为结点）组成，结点可以在运行时动态生成。每个结点包括两个部分：一个是存储数据元素的数据域，另一个是存储下一个结点地址的指针域。 相比于线性表顺序结构，链表比较方便插入和删除操作。   创建头节点 　　手动new一个新的Node，
数据结构讲义：线性表插入算法解析
具体到提供的算法2.3 —— `InsertList`，这是一个在动态链表中插入元素的函数。函数接受三个参数：线性表的头指针`L`，要插入的元素`x`，以及插入位置的索引`I`。算法首先检查插入位置是否合法，即索引I是否在1到...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值