Fermi Estimate

注：本文为 “费米估算” 相关文章合辑。

英文引文机翻，未校。

如有内容异常，请看原文。

---

Fermi Estimate 费米估算

July Thomas, Brilliant Physics, A Former Brilliant Member, and contributed

A Fermi estimate is one done using back-of-the-envelope calculations and rough generalizations to estimate values which would require extensive analysis or experimentation to determine exactly.
费米估计是使用粗略的计算和粗略的概括来完成的估计值，这需要广泛的分析或实验才能准确确定。

Physics is celebrated for its ability to make extremely accurate predictions about tough problems such as the magnetic moment of electrons, the deflection of light by the Sun’s gravity, or the orbit of the planets around the Sun. However, accuracy often comes at the cost of great difficulty in calculation.
物理学因其能够对棘手问题做出极其准确的预测而闻名，例如电子的磁矩、太阳引力引起的光偏转或行星围绕太阳的轨道。然而，准确性往往以计算的巨大难度为代价。

For example, calculating even a poor estimate for the temperature at which a Bose-Einstein condensate forms requires most people about 15 years of preparation, and an accurate calculation for the flight of a commercial jet is entirely intractable without the aid of sophisticated software systems that handle the difficult numerical calculations. If a nice, aesthetically pleasing analytical result were required, much of physics would not have happened. Indeed, the seduction of formal calculations can be a serious hindrance. Whenever the math gets out of hand, it is usually a good idea to relax demands and accept an approach that while imprecise, offers a prayer of moving forward.
例如，即使是对玻色-爱因斯坦凝聚态形成温度的糟糕估计，大多数人也需要大约 15 年的准备，而如果没有处理困难数值计算的复杂软件系统的帮助，商用喷气式飞机飞行的准确计算是完全困难的。如果需要一个漂亮、美观的分析结果，那么很多物理学就不会发生。事实上，正式计算的诱惑可能是一个严重的障碍。每当数学失控时，放宽要求并接受一种方法通常是一个好主意，这种方法虽然不精确，但提供了向前的祈祷。
  ~  

How many windmills are needed to power a country?
一个国家需要多少台风车？

Fermation of subproblems 子问题的费米化

If the cost of the wars in Afghanistan and Iraq were factored into the price of gasoline for a taxpayer in the United States, what would the effective war tax be per gallon? On the basis of energy per person, what is more effective, solar power or wind? How many cracked iPhone screen repairmen are there in the United States? Each of these questions is probably completely bewildering, at least if trying to guess the answer in one step. Who has an intuition for any of these numbers? They are outside normal experience for several reasons. In the context of the question of a war tax
如果阿富汗和伊拉克战争的成本被计入美国纳税人的汽油价格，那么每加仑的有效战争税是多少？根据人均能源，太阳能和风能哪个更有效？美国有多少破裂的 iPhone 屏幕维修工？这些问题中的每一个都可能完全令人困惑，至少如果试图一步猜出答案的话。谁对这些数字有直觉呢？他们超出正常体验有几个原因。在战争税问题的背景下

• Some of the numbers involved are incredibly big, and humans are poor judges of large numbers.
  其中一些涉及的数字非常大，而人类无法判断大数字。
• There are factors that are completely unknown, such as the number of miles driven by a typical person per year, the size of the war’s black budget (clandestine operations), or the stability of OPEC in the absence of United States foreign policy, that could be significant factors in finding an accurate answer.
  有一些因素是完全未知的，例如一个普通人每年驾驶的英里数、战争黑色预算的规模（秘密行动），或者欧佩克在没有美国外交政策的情况下的稳定性，这些因素可能是找到准确答案的重要因素。
• However, these concerns can be addressed by breaking the big problem into appropriate sub-problems.
  但是，可以通过将大问题分解为适当的子问题来解决这些问题。

How much revenue does a typical MLB team make per season? 一支典型的 MLB 球队每个赛季能赚多少收入？

 

---

The main question is quite a tall order, but some reasonable assumptions can be made.
主要问题是一个相当高的要求，但可以做出一些合理的假设。
 
One of the major sources of team revenue must be ticket sales, or else they’d just play the games in one place and broadcast the proceedings to the respective cities. So, assume that ticket sales make up ∼$\frac{1}{3}$ the profits of a typical MLB team (this can always be revisited if it turns out to be wildly off).
球队收入的主要来源之一是门票销售，否则他们只会在一个地方进行比赛，并将比赛过程广播到相应的城市。因此，假设门票销售构成 $\sim \frac{1}{3}$ 典型 MLB 球队的利润（如果结果证明非常糟糕，这总是可以重新审视的）。
 

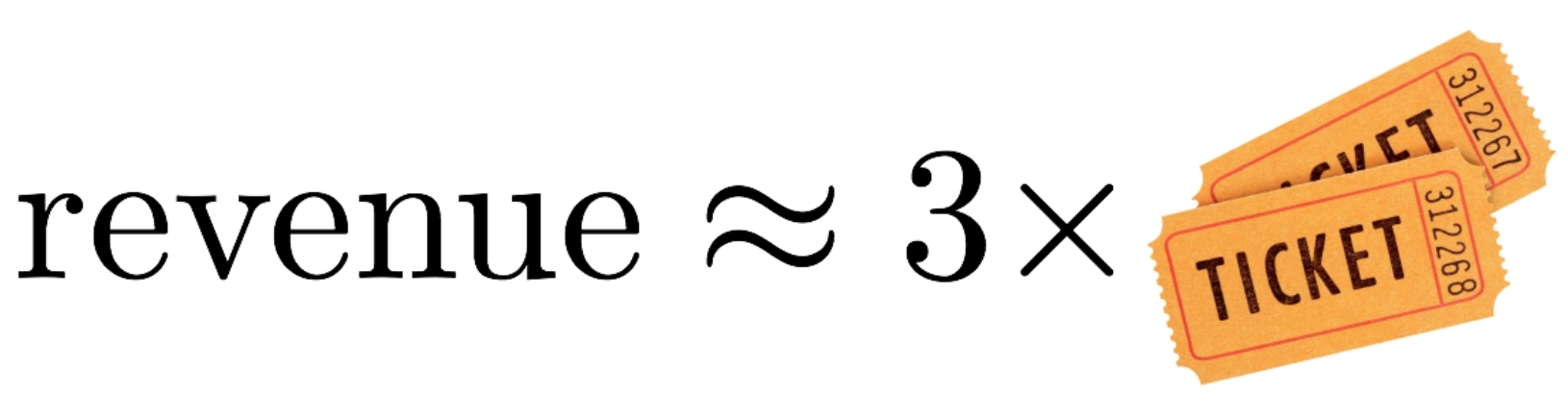
How much does a team make from ticket sales per year? Most MLB stadiums have room for $N_{seat}\approx 40,000$ fans to attend. Assuming that on most days the stadium is approximately$\gamma =80\%$ full, since they probably plan so that the stadium doesn’t look too empty on TV, but has enough room for extra fans should there be heightened interest.
一支球队每年从门票销售中赚多少钱？大多数 MLB 体育场都有空间容纳 $N_{seat}\approx 40,000$ 名粉丝参加。假设在大多数日子里，体育场大约为 $\gamma =80\%$ 满率，因为他们可能计划让体育场在电视上看起来不会太空，但如果兴趣更高，就有足够的空间容纳额外的球迷。
A fan can get a horrible seat for a team in a reasonably sized market for about $20 (personal estimate from going to Los Angeles Angels games). An extremely nice seat can cost as much as $2500. Let’s assume that the distribution is asymmetrical and that most seats are just okay, so that the average ticket costs slightly more than the ultra-bad seat $p_{ticket}\approx$ $30 .
一个球迷可以在一个合理规模的市场中以大约 20 美元的价格为一支球队获得一个可怕的座位（个人估计去看洛杉矶天使队的比赛）。一个非常好的座位可能要花费高达 2500 美元。让我们假设分布是不对称的，并且大多数座位都还可以，因此平均票价比超级糟糕的座位略高于 $p_{ticket}\approx$ $30 。
Finally, each team plays $N_{game}=162$ games per year, and on average, splits the profits of each game with the opposing team. Thus, the annual revenue of a typical MLB team is approximately $3\gamma N_{\text{seat}}{p}_{\text{ticket}}{N}_{\text{game}}\frac{1}{2}\approx$ $230 million.
最后，每支球队都进行比赛 $N_{game}=162$ 场比赛每年，平均而言，与对方球队平分每场比赛的利润。因此，典型 MLB 球队的年收入约为 $3\gamma N_{\text{seat}}{p}_{\text{ticket}}{N}_{\text{game}}\frac{1}{2}\approx$ $230 million。
The real answer is $226 million, which means the estimate is wonderfully accurate, certainly more so than it deserves to be.
真正的答案是 2.26 亿美元，这意味着这个估计非常准确，肯定比它应得的要准确。

Without knowing anything about the actual revenue of any given MLB team, we were able to break the big problem down into several more manageable sub-problems that we could reason about with our common sense:
在对任何给定 MLB 球队的实际收入一无所知的情况下，我们能够将大问题分解为几个更易于管理的子问题，我们可以用我们的常识来推理：

• stadium capacity 体育场容量
• typical attendance 典型出勤率
• ticket prices 票价
• the number of games in a season 一个赛季中的比赛数
• a reasonable guess for the contribution of ticket prices to revenue 对门票价格对收入贡献的合理猜测
   
  By multiplying the answers to all five sub-problems, we arrive at a remarkably good first approximation for team revenue.
  通过将所有 5 个子问题的答案相乘，我们得出了非常好的团队收入第一近似值。
   
  A Fermi problem is an approximate, back-of-the-envelope calculation of an arbitrary figure facilitated by identifying suitable factors of the figure, that are accessible to common experience. Depending on the difficulty of the problem, and the number of sub-problems required to get in touch with common sense, one can usually hope to be correct to within a factor of 2 or 3, and other times to within the correct order of magnitude.
  费米问题是任意图形的近似、粗略的计算，通过确定图形的合适因子来促进，这些因子是常识可以获得的。根据问题的难度，以及与常识取得联系所需的子问题的数量，人们通常希望正确到 2 或 3 倍以内，有时则在正确的数量级内。

0 250 2.5 25,000

You are an astronaut, it is a few hours before you are scheduled to launch for an intergalactic space mission, and you’re sitting on the shore of the Atlantic Ocean near Cape Canaveral, savoring the view one last time. This mission is especially trying; because of the relativistic speed of your spaceship, Earth will be one billion years into the future upon your return.
您是一名宇航员，距离您计划发射星际太空任务还有几个小时，您坐在卡纳维拉尔角附近的大西洋岸边，最后一次欣赏美景。这个任务特别令人费解; 由于你的宇宙飞船的相对论速度，当你回来时，地球将在未来 10 亿年。

Depressed beyond words, you decide, in one of your weaker moments, to pee into the Atlantic Ocean.
难以言喻的沮丧，你决定在你最虚弱的时刻，向大西洋撒尿。

Flash forward: 1 billion years. 快进：10 亿年。

You return to Earth, expecting a hero’s welcome, but instead you find that all of humanity has vanished. Instead, the Earth is run by a peaceful clan of telekinetic dolphins who made off with the lion’s share of Bitcoins that were abandoned by the last humans as they uploaded their souls to the singularity server. In a disillusioned haze, you bend down and fill your astronaut survival cup with refreshing lake water, hoping for some clarity. After drinking the glass, you realize that this far into the future, all the Earth’s water has been thoroughly well mixed since the time you took off on your mission.
你回到地球，期待英雄的欢迎，但你却发现全人类都消失了。相反，地球由一个和平的念力海豚氏族管理，他们偷走了最后一代人类在将灵魂上传到奇点服务器时丢弃的大部分比特币。在幻灭的雾霾中，你弯下腰，把你的宇航员救生杯装满清爽的湖水，希望能得到一些清澈。喝完杯子后，你意识到，在遥远的未来，自从你开始执行任务以来，地球上的所有水都已经彻底混合了。

Approximately how many molecules of your billion year old urine did you just consume?
您刚刚消耗了大约多少个十亿年前的尿液分子？

Assumptions and details 假设和详细信息

• You released $\text{1 L}$ of urine into the Atlantic Ocean.
  你释放了 $\text{1 L}$ 尿液进入大西洋。

• Approximate your urine as consisting of pure water.
  你的尿液近似由纯水组成。

How many iPhone screen repairmen are there in the United States?
美国有多少名 iPhone 屏幕维修工？

An important number for this problem is the number of iPhones in the United States. We can arrive at this number in two ways.
这个问题的一个重要数字是美国的 iPhone 数量。我们可以通过两种方式得出这个数字。

First, from common experience, it seems about 1 in 2 people has a smartphone, and those without them tend to be the very young or the very old. Furthermore, it is common to hear that Android phones dominate the market place, so let’s estimate the Android figure to be about $\frac{2}{3}$, and thus the iPhone share to be about $\frac{1}{3}$, approximating Windows, Blackberry, and other platforms to be minor players in the market. This yields $\sim 50,000,000$ iPhones.
首先，从一般经验来看，似乎大约每 2 个人中就有 1 人拥有智能手机，而没有智能手机的人往往是非常年轻或非常年长的人。此外，经常听到 Android 手机在市场上占据主导地位，因此让我们估计 Android 的数字约为 $\frac{2}{3}$，因此 iPhone 份额大约是 $\frac{1}{3}$，将 Windows、Blackberry 和其他平台近似为市场上的次要参与者。这样就会得到 $\sim 50,000,000$ 部 iPhone。

Another way is to think about the people you see on the street, and try to directly estimate how many of them have an iPhone. This number seems to me to be around 1 in every 5 people, which would make ∼60∼60 million iPhones in the country. Thus, an estimate in the range of fifty to sixty million seems to be approximately right.
另一种方法是想想你在街上看到的人，并尝试直接估计他们中有多少人拥有 iPhone。在我看来，这个数字大约是每 5 人中就有 1 人，这将使 ∼60 该国有 6000 万部 iPhone。因此，5000 万到 6000 万之间的估计似乎大致正确。

How many of these are cracked? Phone contracts usually last for two years, and most people take their upgrade, so let’s assume that the typical iPhone spends 2.5 years with the customer before being replaced. Now, how many of these screens will be cracked over the lifetime of the phone? I’d guess that this number sits somewhere around 20%.
其中有多少是破解的？电话合同通常持续两年，大多数人都会进行升级，所以让我们假设典型的 iPhone 在被更换之前与客户在一起会花 2.5 年。现在，在手机的整个生命周期内，这些屏幕中会有多少被破解？我猜这个数字在 20% 左右。

Every cracked screen doesn’t get replaced or else we wouldn’t see them around too often. Let’s assume that if a crack happens in the first $\frac{2}{3}$ of the time for which the customer owns the phone, they’ll get it fixed, but otherwise they’ll just wait for a new phone. This means that in a given year, $\frac{1\text{ iPhone}}{2.5\text{ years}}\times 20\%\times 66\%\approx 5\%$ of iPhones will need their screens replaced, or $5\%\times 55,000,000\approx 2,800,000$ iPhone screens.
每个破裂的屏幕都不会被更换，否则我们不会经常看到它们。我们假设，如果第一个 $\frac{2}{3}$ 客户拥有手机的时间，他们会修好它，但除此之外，他们只会等待新手机。这意味着，在给定的年份中， $\frac{1\text{ iPhone}}{2.5\text{ years}}\times 20\%\times 66\%\approx 5\%$ 的 iPhone 需要更换屏幕，或者 $5\%\times 55,000,000\approx 2,800,000$ 个 iPhone 屏幕。

How many repairmen does this support? Let us assume that each iPhone screen takes the average repairmen 1 hr1 hr to fix and that the average iPhone screen fixer spend about half their full time work week fixing iPhone screens (averaging over full and part time workers). Thus, we predict there to be enough broken iPhones to support the employment of approximately $\frac{2.8\times 10^6\text{ phones}\times (1\text{ hr/phone})}{52\text{ weeks}\times 20\text{ hrs/(iPhone fixer)/week}}\approx 2,700\text{ iPhone fixers}$ iPhone fixers in the entire country.
这支持多少维修工？让我们假设每个 iPhone 屏幕都需要普通的维修工 1 小时 1 小时来修复，并且 iPhone 屏幕修复者平均花费大约一半的全职工作时间来修复 iPhone 屏幕（全职和兼职工人的平均人数）。因此，我们预测将有足够多的破损 iPhone 来支持大约 $\frac{2.8\times 10^6\text{ phones}\times (1\text{ hr/phone})}{52\text{ weeks}\times 20\text{ hrs/(iPhone fixer)/week}}\approx 2,700\text{ iPhone fixers}$ iPhone 修复者 在全国。

This is roughly 10 times the number of Apple stores in the country, so it seems fairly reasonable.
这大约是该国 Apple 商店数量的 10 倍，因此似乎相当合理。

The accuracy of guess strings guess 字符串的准确性

As we saw with the MLB revenue problem, breaking down our big problems into small problems can be a big aid in tackling an estimate. However, there is potential for trouble. For instance, with the iPhone we are not necessarily getting more familiar with the numbers we have to estimate by breaking the problem down. Despite the number of cracked iPhone screens being a simpler problem than guessing the number of screen repairmen outright, few people are familiar with the frequency of iPhone screen breaks. We hope this number will be accurate to within a factor of two (we guessed 20% but it could easily be 10% or 30%). Similarly, we took a wild guess at the amount of time required to fix a given iPhone. As it turns out, the true frequency of screen breaks is close to one third of all iPhones and the average repair time is closer to half an hour. Thus in one of the numbers we were too low by a factor of $\frac{2}{3}$ and in another we were too high by a factor of two, which means that all told, those two factors place us about 33% too high in our estimate. With long strings of guesses, these errors can multiply, and drag us away from the right answer. However, we are unlikely to have a consistent bias (too high or too low) on a series of unique sub-problems, and thus, our mistakes will tend to balance each other out, as in a random walk. If we are too high in some numbers, we are likely to be too low in other numbers.
正如我们在 MLB 收入问题中看到的那样，将我们的大问题分解为小问题对解决估算有很大帮助。但是，可能会有麻烦。例如，对于 iPhone，我们不一定会更熟悉我们必须通过分解问题来估计的数字。尽管破裂的 iPhone 屏幕数量比直接猜测屏幕维修工的数量更简单，但很少有人熟悉 iPhone 屏幕破裂的频率。我们希望这个数字能精确到两倍以内（我们猜测是 20%，但也很容易是 10% 或 30%）。同样，我们对修复给定 iPhone 所需的时间进行了大胆的猜测。事实证明，屏幕破裂的真实频率接近所有 iPhone 的三分之一，平均维修时间接近半小时。因此，在其中一个数字中，我们太低了 $\frac{2}{3}$ 而在另一个 Factor 中，我们高出了 2 倍，这意味着总而言之，这两个因素使我们差不多 33% 在我们的估计中太高了。在一长串的猜测中，这些错误可能会成倍增加，并使我们远离正确的答案。然而，我们不太可能在一系列独特的子问题上有一致的偏见（太高或太低），因此，我们的错误往往会相互平衡，就像在随机游走中一样。如果我们在某些数字上太高，那么我们在其他数字上也可能太低。

Crudely, if we have a consistent uncertainty in estimating any numbers, we can model our guess as a random number drawn from a Gaussian distribution about the true answer with a characteristic variance ${\sigma }^2$. Breaking our guess into $n$ sub-problems means that our variance becomes $\approx n{\sigma }^2$ (the variance of random variables is additive), and thus the standard deviation (the square root of the variance) increases with the square root of $n$. This is the same behavior as a random walk (where the average displacement increases as $\sqrt{t}$ with time), which we might expect since we hope to guess slightly too high or slightly too low at each number we estimate. Thus, when possible, we should avoid making too many sub-guesses.
粗略地说，如果我们在估计任何数字时都有一致的不确定性，我们可以将我们的猜测建模为从高斯分布中抽取的关于真实答案的随机数，该随机数具有特征方差 ${\sigma }^2$ .将我们的猜测分解为 $n$ 个子问题意味着我们的方差变为 $\approx n{\sigma }^2$ （随机变量的方差是加法的），因此标准差（方差的平方根）随着 $n$.这与随机游走的行为相同（其中平均位移随着时间的推移增加 $\sqrt{t}$ ），这可能是我们预期的，因为我们希望在我们估计的每个数字上猜测稍微过高或稍微过低。因此，如果可能，我们应该避免进行过多的子猜测。

On the other hand, it is likely that our familiarity with the numbers in our sub-problems is significantly better than our knowledge of our big problem, so to a point it will always make sense to break up our big problems. It isn’t possible to precisely model this trade-off between random walks and accurate knowledge, so knowing when to stop finding sub-problems is a matter of intuition and building experience in making accurate predictions of this kind.
另一方面，我们对子问题中数字的熟悉程度可能明显优于我们对大问题的了解，因此在某种程度上，分解我们的大问题总是有意义的。不可能在随机游走和准确知识之间精确建模这种权衡，因此知道何时停止查找子问题是直觉问题，并需要积累做出此类准确预测的经验。

Dominant Part 主导部分

Another crucial technique in good estimates is to ignore everything but what you deem to be the most important factor(s) in the problem. In the baseball problem, for example, we assumed the major sources of revenue to be tickets, TV, and the merchandise that people buy at the stadium or elsewhere, and we took all other sources of income to be negligible. Likewise, if we estimate the daily energy budget of a person, we can assume that the energy used by their electric toothbrush makes a negligible contribution when compared with the energy that goes into making their food, driving their vehicle, heating their home, etc. If we consider the time required to get in a car and drive 100 miles, we can ignore the time required to open the door, et cetera.
良好估计的另一个关键技术是忽略所有内容，除了您认为是问题中最重要的因素。例如，在棒球问题上，我们假设主要收入来源是门票、电视以及人们在体育场或其他地方购买的商品，而我们认为所有其他收入来源都可以忽略不计。同样，如果我们估计一个人的日常能源预算，我们可以假设他们的电动牙刷使用的能源与制造食物、驾驶车辆、取暖等的能源相比，其贡献可以忽略不计。如果我们考虑上车行驶 100 英里所需的时间，我们可以忽略开门所需的时间，等等。

This takes some bravado to get started. Getting a sense for the dominant contribution(s) is not always obvious and may take some numerical comparisons to get a good sense for it. However, reducing the number of variables we need to keep track of always reduces the complexity of our mathematical problems, and can lead us toward more accurate solutions. For example, if we solve a problem first in one extreme case, then in another, we may be able to identify the short and long time behavior, or low and high energy behavior, and therefore know what we should be looking for when we undertake the full-blown analytical solution. Treating the dominant parts leads us to answers that are substantially correct, i.e. only differ from the true answer by a factor of twenty or thirty percent, and therefore give us a good idea of what’s going on.
这需要一些虚张声势才能开始。了解主要贡献并不总是显而易见的，可能需要进行一些数值比较才能很好地了解它。然而，减少我们需要跟踪的变量数量总是可以降低数学问题的复杂性，并且可以引导我们找到更准确的解决方案。例如，如果我们在一个极端情况下先解决一个问题，然后在另一个极端情况下，我们可能能够识别短时和长时间的行为，或者低能量和高能量行为，因此知道当我们进行全面的分析解决方案时应该寻找什么。处理主导部分会引导我们得出基本正确的答案，即与真实答案仅相差 20% 或 30 倍，因此让我们对发生的事情有一个很好的了解。

How long will it take to melt a frozen water bottle by shaking it?
摇晃冷冻的水瓶需要多长时间才能融化？
 

To make this estimate, we have to identify a mechanism for heating the ice. For simplicity, we assume that the system is at zero degrees Celsius. Under this assumption, we can’t melt the ice if there’s none melted to begin with, i.e. if we shake a solid block of ice back and forth, no heat is delivered to the ice.
为了做出这个估计，我们必须确定一种加热冰的机制。为简单起见，我们假设系统处于 0 摄氏度。在这个假设下，如果一开始就没有融化的冰，我们就无法融化冰，也就是说，如果我们来回摇晃一块实心冰块，就不会有热量传递到冰上。

To make progress, let’s grant the water bottle a small initial volume of liquid water, also at zero degrees Celsius. Let’s say assume that a water bottle has volume $V=1\text{ L}$ and that initially, some small fraction of the water is liquid, i.e. $ϵ=0.1\%$.
为了取得进展，让我们给水瓶少量的初始液态水，也是在零摄氏度。假设一个水瓶的体积 $V=1\text{ L}$，最初，一小部分水是液体，即 $ϵ=0.1\%$.
 
When we accelerate the bottle in one direction, all the material in the bottle is given kinetic energy. When we decelerate to force the bottle in the other direction, the ice is decelerates by traveling through the liquid water and the liquid water essentially moves out of the way to the back of the bottle. This is the manner in which heat enters the system. In decelerating through the liquid water, the ice experiences a frictional force that’s converted into heat. Since the ice and water are at zero degrees Celsius, the heat goes toward melting the ice.
当我们向一个方向加速瓶子时，瓶子中的所有材料都会被赋予动能。当我们减速以迫使瓶子向另一个方向移动时，冰通过液态水而减速，液态水基本上会移开到瓶子的背面。这就是热量进入系统的方式。在通过液态水减速时，冰会受到摩擦力，该摩擦力会转化为热量。由于冰和水处于零摄氏度，热量会融化冰。
 
At time $t$ the liquid volume is given by $V(t)$, and the volume of frozen ice is given by $V_T-V(t)$ (in this step, we explicitly ignore the density difference of ice and water). If we approximate the water bottle as a cylinder, the distance that the ice will decelerate through is given by the liquid volume divided by the cross-sectional area: $A^{-1}\left(V_T-V(t)\right)$. Let us make the crude approximation that the ice doesn’t lose any velocity as it pushes the water out of the way, i.e. the accelerating force from our arm is equal to the force of water friction on the ice. Thus the ice travels at the speed $v$ until it hits the end of the bottle. Let’s assume a vigorous shake. The human arm is capable of throwing a ball (baseball, cricket) at ∼40 m/s∼40 m/s; let’s take 10% of that value as the sustained steady state velocity of the ice, $v\approx 4\text{ m/s}$.
时间 $t$ 液体体积为 $V(t)$ , 冻结的体积由下式给出 $V_T-V(t)$ （在此步骤中，我们明确忽略了冰和水的密度差异）。如果我们将水瓶近似为圆柱体，则冰减速通过的距离由液体体积除以横截面积得出： $A^{-1}\left(V_T-V(t)\right)$ 。让我们粗略地估计一下，冰在将水推开时不会损失任何速度，即我们手臂的加速力等于水在冰上的摩擦力。因此，冰以 $v$ 直到它碰到瓶子的末端。让我们假设剧烈摇晃。人类的手臂能够向 ∼40 米/秒 ∼40 米/秒;让我们将该值的 10% 作为冰的持续稳态速度 $v\approx 4\text{ m/s}$。
 
Then, with each shake, our ice feels the drag force $\approx \frac{1}{2}{\rho }_{water}A{v}^2$ which acts through the distance $A^{-1}\left(V_T-V(t)\right)$, thus with each shake, our bottle acquires the heat $\approx \frac{1}{2}{\rho }_{water}{v}^2\left(V_{T}V(t)\right)$.
然后，每次摇晃时，我们的冰都会感受到阻力 $\approx \frac{1}{2}{\rho }_{water}A{v}^2$ 它通过距离起作用 $A^{-1}\left(V_T-V(t)\right)$，因此每次摇晃时，我们的瓶子都会获得热量 $\approx \frac{1}{2}{\rho }_{water}{v}^2\left(V_{T}V(t)\right)$ 。
 
We can turn this into an average power by estimating the time taken to decelerate through the water. Here we have several choices. We can make a simplistic model in which each shake travels through the same distance dd and is shaken back and forth at the speed vv. We can also make a slightly more sophisticated model in which the shaker changes directions as soon as they feel the ice hit the bottle. This is more realistic. First we’ll calculate the simple model.
我们可以通过估计在水中减速所需的时间，将其转换为平均功率。在这里，我们有几种选择。我们可以制作一个简单的模型，其中每次摇动都经过相同的距离 d d 并以 v v. 我们还可以制作一个稍微复杂的模型，其中摇床一旦感觉到冰块碰到瓶子就改变方向。这更现实。首先，我们将计算简单模型。
 
Constant shake frequency
恒定的摇动频率

Here, we have it that shake time is given by $t\approx d/v$, and thus the average power is given by
 
$\bar{P}=\frac{1}{2}\frac{V_{T}V(t)}{d}{\rho }_{water}{v}^3$

在这里，我们有 shake time 的给出 $t\approx d/v$，因此平均功率由下式给出
 
$\bar{P}=\frac{1}{2}\frac{V_{T}V(t)}{d}{\rho }_{water}{v}^3$

How much ice melts with the addition of heat $\Delta Q$? The heat of melting is given by $L_{melt}$, and we therefore require the heat $\Delta Q=M_{ice}{L}_{melt}$ to melt the mass $M_{\text{ice}}$ of ice. Taking a time derivative, we have ${\dot{M}}_{\text{ice}}=\frac{\bar{P}}{L_{\text{melt}}}$, or

$\dot{V}(t)=\frac{\bar{P}}{{\rho }_{\text{ice}}{L}_{\text{melt}}}$

$=\frac{1}{2}\frac{{\rho }_{\text{water}}{v}^3}{d{\rho }_{\text{ice}}{L}_{\text{melt}}}\left(V_T-V(t)\right)$,

加热后冰融化了多少 $\Delta Q$。熔化热由下式给出 $L_{melt}$ 融化 ，因此我们需要热量 $\Delta Q=M_{ice}{L}_{melt}$ 熔化质量 $M_{\text{ice}}$。以时间导数为例，我们有 ${\dot{M}}_{\text{ice}}=\frac{\bar{P}}{L_{\text{melt}}}$ 或

$\dot{V}(t)=\frac{\bar{P}}{{\rho }_{\text{ice}}{L}_{\text{melt}}}$
 
$=\frac{1}{2}\frac{{\rho }_{\text{water}}{v}^3}{d{\rho }_{\text{ice}}{L}_{\text{melt}}}\left(V_T-V(t)\right)$,
 
which yields the solution

$V(t)=V_T+\left(V(0)-V_T\right)e^{-t\gamma }$，

从而产生解决方案

$V(t)=V_T+\left(V(0)-V_T\right)e^{-t\gamma }$，
 
where $\gamma =\frac{1}{2}\frac{{\rho }_{water}{v}^3}{d{\rho }_{ice}{L}_{melt}}$. Solving for the time $t$ at which the fraction $f$ of the ice has melted (explained below), we find

$t_{\text{melt}}={\gamma }^{-1}\log \frac{1-ϵ}{1-f}$.
 
其中 $\gamma =\frac{1}{2}\frac{{\rho }_{water}{v}^3}{d{\rho }_{ice}{L}_{melt}}$。解出部分冰融化的时间 $t$ 的分数 $f$ 的冰已经融化（解释如下），我们发现

$t_{\text{melt}}={\gamma }^{-1}\log \frac{1-ϵ}{1-f}$
 
This solution is asymptotic as we approach complete melting, so we have to use some reasonable cutoff, such as $f=0.99$, i.e. the time to melt 99% of the ice. Plugging in the known values for the density of ice, and water, the heat of melting, some reasonable value for $d$(0.5 m), and $V=1\text{ L}$ (volume of a typical water bottle), we get $\approx 20,000\text{ s}$ or about $5.5\text{ hrs}$. Since we shake at roughly $8\text{ Hz}$, this translates to about 160,000 shakes back and forth. Below, we plot the number of shakes required as ϵϵ (the initial fraction of melted ice) is varied from 0.1% to 99%.
当我们接近完全熔化时，这个解是渐近的，所以我们必须使用一些合理的截止值，例如 $f=0.99$，即融化 99% 的冰的时间。代入冰的密度和水的已知值，融化的热量，一些合理的值 d d （0.5 m） 和 $V=1\text{ L}$（典型水瓶的体积），我们得到 ≈20,000 秒 ≈20,000 秒或左右 5.5 小时由于我们大致摇晃 $8\text{ Hz}$ ，这相当于来回摇晃大约 160,000 次。下面，我们将所需的摇动次数绘制为 ε ε（融化冰的初始分数）从 0.1% 到 99% 不等。
 
Our choice for tt was poor because shakes at the beginning should have a higher frequency (short distance for ice to travel through liquid) while shakes at the end should have a lower frequency (greater distance to travel). Thus, initially, this model should underestimate the average power delivered, and as time goes on, it may overestimate it.
我们的选择 t T 很差，因为开始时的震动应该具有较高的频率（冰在液体中的移动距离较短），而结束时的震动应该具有较低的频率（移动距离较远）。因此，最初，该模型应该低估提供的平均功率，随着时间的推移，它可能会高估它。

Scaled shake frequency
缩放的摇动频率
 
Now we calculate the model where we change shake direction as soon as the ice hits the end of the bottle. The time it takes to hit the end in this case is given by $t\approx \frac{\left(V_{T}V(t)\right)A^{-1}}{v}$.
现在我们计算一个模型，一旦冰块碰到瓶子的末端，我们就会改变摇晃方向。在这种情况下，到达终点所需的时间由下式给出 $t\approx \frac{\left(V_{T}V(t)\right)A^{-1}}{v}$。
 
Using this new estimate for $t$, we find the average power to be constant in time
使用这个新的估计值 $t$，我们发现平均功率在时间上是恒定的

$\bar{P}=\frac{1}{2}{\rho }_{\text{water}}{v}^2\frac{V_T-V(t)}{V_T-V(t)}Av$

$=\frac{1}{2}\rho v^{3}A$.
This yields a much simpler result, i.e. $V(t)=\frac{1}{2}\frac{{\rho }_{water}}{{\rho }_{ice}{L}_{melt}}{v}^{3}At$, and thus $t\approx \frac{2V_T{\rho }_{ice}{L}_{melt}}{{\rho }_{water}{v}^{3}A}$

这会产生一个更简单的结果，即 $V(t)=\frac{1}{2}\frac{{\rho }_{water}}{{\rho }_{ice}{L}_{melt}}{v}^{3}At$ ，因此 $t\approx \frac{2V_T{\rho }_{ice}{L}_{melt}}{{\rho }_{water}{v}^{3}A}$。
 
Plugging in the numbers, we predict that we will require only $\approx 2000s$, or 30 min. The average shake will last for $t_{shake}\approx \frac{V_T}{2A}\frac{1}{v}=0.025s$, which is about $40\text{ Hz}$, so we require $\approx 80,000$ shakes.
插入这些数字，我们预测我们只需要 $\approx 2000s$ 或 30 分钟平均摇晃将持续 $t_{shake}\approx \frac{V_T}{2A}\frac{1}{v}=0.025s$，大约是 $40\text{ Hz}$，所以我们需要 $\approx 80,000$ 次摇晃。
 
Are these reasonable estimates for the number of shakes to melt a frozen water bottle? When should we expect these models to work? Are there any cases where this model should fail terribly, i.e. should it be accurate for small initial unmelted volume?
这些对于融化冰冻水瓶的摇动次数是否合理估计？我们应该期望这些模型何时起作用？是否有任何情况会导致此模型严重失败，即对于较小的初始未熔化体积，它是否应该准确？
 
Challenge yourself 挑战自我

How long would it take for you to shake the melted ice from zero degrees Celsius up to boiling?
您将融化的冰从零摄氏度摇晃到沸腾需要多长时间？

Wars in the Middle East 中东战争

  ~  

Often, when pressed for an explanation of the western military presence in the Arabian peninsula, government officials will point to the “strategic interests” of the west in the economic balance and stability of Middle East oil powers, the implication being that without constant intervention in this part of the world, oil markets would become unstable and the west would suffer economically. Putting aside the risks or lack thereof that would exist in a world with a hands-off foreign policy toward the Arabian Peninsula, this begs the question of just how much money our military presence in the Middle East has cost relative to the western consumption of oil. For simplicity, we’ll consider the United States.
通常，当被要求解释西方在阿拉伯半岛的军事存在时，政府官员会指出西方在中东石油大国的经济平衡和稳定中的“战略利益”，这意味着如果不对世界这一地区的持续干预，石油市场将变得不稳定，西方将在经济上受到影响。撇开一个对阿拉伯半岛采取不干涉外交政策的世界存在的风险或缺乏风险不谈，这就引出了一个问题，即相对于西方的石油消费，我们在中东的军事存在究竟要花多少钱。为简单起见，我们将考虑美国。

First we estimate the number of gallons of gasoline that the U.S. consumes every year. Let’s approximate the gas used in cars to be roughly half of all gasoline consumed in the United States. Next, let’s estimate the number of miles driven per year by the average American. From personal experience, it seems reasonable to take 40 miles as the average distance driven per day by Americans in their commute to and from work. Counting $365\times \frac{5}{7}\approx 260$ work days (ignoring holidays), this makes

$260\text{ workdays}\times 40\text{ miles per workday}\approx 10,000\text{ miles per year}$.
首先，我们估计美国每年消耗的汽油加仑数。让我们估计汽车使用的汽油大约占美国所有汽油消耗量的一半。接下来，让我们估计一下普通美国人每年驾驶的英里数。从个人经验来看，将 40 英里作为美国人每天上下班通勤的平均行驶距离似乎是合理的。计数 $365\times \frac{5}{7}\approx 260$ （不计节假日)，这使得
$260\text{ workdays}\times 40\text{ miles per workday}\approx 10,000\text{ miles per year}$。

Let’s multiply that by $\frac{3}{2}$ that to account for leisure, and errands. That brings us to ≈15,000≈15,000 miles per year. Assuming that $\frac{3}{5}$ of the country’s population is in the active work force, this makes $180,000,000$ people driving $\approx 15,000$ miles a year, or $2.7\times 10^{12}$ miles driven per year. Assuming a typical gas mileage of 25 miles per gallon, this gets us to $1.1\times 10^{11}$ gallons of per year, or $2.2\times 10^{11}$ gallons per year all told.
让我们将其乘以 $\frac{3}{2}$ 考虑到闲暇和差事。这就把我们带到了每年 $\approx 15,000$ 英里。假设该国 $\frac{3}{5}$ 的人口是活跃的劳动力，这使得 $180,000,000$ 人驾驶 每年 15,000 英里，或 $2.7\times 10^{12}$ 每年行驶英里数。假设典型的油耗为每加仑 25 英里，这使我们达到 $1.1\times 10^{11}$ 加仑数，或 $2.2\times 10^{11}$ 加仑数。

Over the period from 2001-2007 years, the portion of the military budget of the United States devoted to force projection in the Persian Gulf has averaged about $ $5\times10^{11}$ per year, which means that over that timespan there was an unseen tax on gasoline equivalent to roughly
$\displaystyle\approx\frac{$5\times10^{{11}}{2.2\times10}{11}\text{ gallons}}\approx$2\text{ per gallon}$

在 2001 年至 2007 年期间，美国军事预算中用于波斯湾力量投射的部分平均约为每年 KaTeX parse error: Undefined control sequence: \5 at position 14: \displaystyle\̲5̲\times10^{11} 美元，这意味着在这段时间内，有一项看不见的汽油税，大约相当于
$\displaystyle\approx\frac{$5\times10^{{11}}{2.2\times10}{11}\text{ gallons}}\approx$2\text{ per gallon}$

Taking the popular rationale for Middle East foreign policy at face value, you might expect that the domestic cost of gasoline would have fallen by some amount during this effort or remained stable, but in fact the cost of gasoline rose considerably. The price of oil is the outcome of a complex interconnection of supply and demand, international trade, and the capriciousness of OPEC, but it is also a function of the stability of the region. Invariably, some of the price increase was due to the massive instability visited upon the region by the sustained wars and insurgency movements that rose up in opposition to them.
从表面上看中东外交政策的流行理由，你可能会认为国内汽油成本会下降一些或保持稳定，但实际上汽油成本大幅上升。石油价格是供需、国际贸易和欧佩克反复无常的复杂相互联系的结果，但它也是该地区稳定的函数。无一例外，一些价格上涨是由于持续的战争和反对他们的叛乱运动给该地区带来了巨大的不稳定。

Though the connection between the wars and the pump is concealed by the shell game of how taxes are paid, common sense calculation can shine a light on the true cost and sense of military interventions.
尽管战争与加油站之间的联系被如何纳税的空壳游戏所掩盖，但常识性计算可以揭示军事干预的真实成本和意义。
  ~  

Suppose you’re flying from San Francisco (SFO) to New York (NYC). The plane (Airbus 320) carries 189 passengers and has 6 crew members who each make $20 per hour. Assume a minimal model where the only costs of operating the flight are paying the salary of the crew, and paying for fuel. Further, assume that the all the engine does is fight the drag force. If each ticket costs $300, jet fuel costs $0.75 per liter, and the crew is paid for the number of complete hours they work, what percent of your ticket price goes toward the airline’s profit?
假设您从旧金山 （SFO） 飞往纽约 （NYC）。这架飞机（空客 320)载有 189 名乘客，有 6 名机组人员，每人每小时赚 20 美元。假设一个最小模型，其中运营航班的唯一成本是支付机组人员的工资和燃料费用。此外，假设发动机所做的只是对抗阻力。如果每张机票价格为 300 美元，喷气燃料每升价格为 0.75 美元，机组人员根据他们工作的完整小时数获得报酬，那么您的机票价格中有多少百分比用于航空公司的利润？
Assumptions and Details 假设和详细信息

• The Airbus has a drag coefficient $C_D$ of $\frac{1}{3\pi }$.
  空客有一个阻力系数 $C_D$ of $\frac{1}{3\pi }$.

• The density of air is $\rho =1.275{\text{ kg/m}}^3$.
  空气的密度为 $\rho =1.275{\text{ kg/m}}^3$

• The plane flies at $511\text{ mph }(228\text{ m/s})$ from start to finish.
  飞机巡航 511 英里/小时（228 米/秒） 从开始到结束。

• The distance from NYC to SFO is $4148\text{ km}$.
  NYC 到 SFO 的距离是 4148 公里

• The energy efficiency of the jet engines is $\eta =16\%$.
  喷气发动机的能源效率 $\eta =16\%$

• Approximate the Airbus as a cylinder of diameter $6\text{ m}$.
  将 Airbus 近似为直径为 6 米

• The energy density of the jet fuel is $45\times 10^6\text{ J/kg}$.
  喷气燃料的能量密度为 $45\times 10^6\text{ J/kg}$

• The density of the fuel is $804{\text{ kg/m}}^3$.
  燃料的密度为 $804{\text{ kg/m}}^3$

• The crew is paid for each full hour they work, i.e. if they work $5.2hrs$ they are paid for $5.5$.
  机组人员每工作一小时就会得到报酬，即如果他们工作 5.2 小时付 5.5.

Scaling of wind and solar power 风能和太阳能的规模化

Wind power 风能

A favored technology of some environmentalists is the wind farm. Its advocates point out how it is inherently clean and carbon neutral, and that the wind is a resource we’re leaving on the table. Together with the circumstance of our current reliance on petroleum, wind seems like a slam dunk. But how does it compare with competing renewable energy sources like solar power? How do its intrinsic limitations compare with those of the Sun?
一些环保主义者青睐的技术是风电场。它的倡导者指出，风能本质上是清洁和碳中和的，而且风能是我们要留给桌面上的一种资源。再加上我们目前对石油的依赖，风似乎是一个大灌篮。但它与太阳能等竞争性可再生能源相比如何？它的内在限制与太阳相比如何？
 
In order to have a sense of scale for our energy budget, we need to know the daily energy use per person. Let’s take the European Union states as a middle of the road energy-using population. Official figures state that energy use for E.U. citizens is approximately 40,000 kilowatt-hours per person per year, or $112\text{ kWh}$ per person per day. This number is fun to estimate on its own, but we’ll take it for granted for the purposes of our present question.
为了对我们的能源预算有一个尺度感，我们需要知道每人每天的能源使用量。让我们以欧盟国家为例，作为能源使用人口的中间地带。官方数据表明，欧盟公民的能源使用量约为每人每年 40,000 千瓦时，或 每人每天 112 kWh。这个数字本身估计起来很有趣，但就我们目前的问题而言，我们将认为它是理所当然的。
 
When we think of a windmill, the basic thing that’s happening is that the kinetic energy of the wind is being harvested to spin the windmill which uses the kinetic energy to drive an electric generator. The amount of kinetic energy that’s in a parcel of wind of volume $V$ and velocity $v$ is given by $\frac{1}{2}\rho V{v}^2$. If we assume that the only wind that drives the propeller is that wind that’s in the cylinder of air aligned with the blades, then we have $\frac{1}{2}\rho Av{v}^2=\frac{1}{2}\rho A{v}^3$ kilowatts arriving at the blades per second. Thus, in a day, we have $\frac{1}{2}\rho A{v}^3\times 24$

kilowatt-hours flowing through the blades.
当我们想到风车时，发生的基本事情是风的动能被收集起来，使风车旋转，风车利用动能驱动发电机。体积风中的动能 V 和速度 v 的给出公式为 $\frac{1}{2}\rho V{v}^2$ 。如果我们假设驱动螺旋桨的唯一风是与叶片对齐的空气圆柱体中的风，那么我们就有 $\frac{1}{2}\rho Av{v}^2=\frac{1}{2}\rho A{v}^3$ 每秒到达叶片的千瓦数。因此，在一天之内，我们有 $\frac{1}{2}\rho A{v}^3\times 24$ 千瓦时流经叶片。
 
Now, the density of air in the European Union is $\approx 1.3{\text{ kg/m}}^2$, and the average wind speed in the European Union is about $5\text{ m/s}$. Taking the blade area to be $A\approx 3r^2$, we have $\frac{3}{2}\rho v^3{r}^2\times 24\text{ hrs}$ kilowatt-hours coming from a windmill.
现在，欧盟的空气密度是 $\approx 1.3{\text{ kg/m}}^2$ ，欧盟的平均风速约为 $5\text{ m/s}$。将刀片区域 $A\approx 3r^2$ 我们有 $\frac{3}{2}\rho v^3{r}^2\times 24\text{ hrs}$ 来自风车的千瓦时。
 
Finally, windmills are not completely efficient not only because the wind has kinetic energy left when it leaves the blades. Let’s be generous and assume that windmills can harvest $50\%$ of the energy that flows through them.
最后，风车并不完全有效，不仅因为风离开叶片时还残留了动能。让我们慷慨地假设风车可以收集流经它们的 50% 的能量。

Since the windmill operates by taking energy out of the air, we can’t put one windmill directly behind another or we’ll quickly end up with a region of dead air. Hence, we must put a reasonable amount of space between our windmills. To estimate how far this is, look at some pictures of wind farms in the wild. For example, in the picture below, it appears that the spacing between windmills is roughly 6 times the size of the blade diameter.
由于风车是通过从空气中获取能量来运作的，我们不能将一个风车直接放在另一个风车后面，否则我们很快就会变成一个死气沉沉的区域。因此，我们必须在风车之间留出合理的空间。要估计这有多远，请看一些野外风电场的照片。例如，在下图中，风车之间的间距大约是叶片直径大小的 6 倍。
 
Thus, a dense packing of the windmills would have one windmill for every ${\left(12r\right)}^2=144r^2{\text{ meters}}^2$. Being extremely generous and taking the entirety of the land mass of the European Union ($\approx 4.5\times 10^6{\text{ km}}^2$) to be ripe for windmill placement, this gives us $\frac{3}{4}\rho v^3\times 24\text{ hrs}\frac{1}{144}{A}_{E.U.}$. kilowatt-hours per day. Plugging in real numbers, this gives about $1{\text{ W/m}}^2$ or $200\text{ kWh}$ per person per day. Being a bit more realistic, we could probably only place windmills on about $20\%$ of the land area of the European Union when we consider mountains, places that aren’t so windy, that people don’t want their land covered by windmills, etc.
因此，一个密集的风车堆积将有一个风车对应一个 ${\left(12r\right)}^2=144r^2{\text{ meters}}^2$ 。极其慷慨并占据了欧盟的全部土地（ $\approx 4.5\times 10^6{\text{ km}}^2$ ） 放置风车的时机成熟，这给了我们 $\frac{3}{4}\rho v^3\times 24\text{ hrs}\frac{1}{144}{A}_{E.U.}$每天千瓦时。代入实数，得到大约 $1{\text{ W/m}}^2$ or $200\text{ kWh}$ 每人每天。更现实一点，我们可能只能将风车放在大约 20% 当我们考虑山脉时，占欧盟陆地面积的 20%，这些地方没有那么多风，人们不希望他们的土地被风车覆盖，等等。
 
Windmills are more often useless than not during the day, with most E.U. windmills operating at something like $25\%$ capacity. This brings us down to about $200/20=10\text{ kWh/day}$ per person, which is about 10% of the typical E.U. citizen’s energy budget. Altogether, this isn’t bad, but it also isn’t a solution to an energy crisis.
风车通常比白天无用多，大多数欧盟风车的运行时间类似于 25% 容量。这使我们归结为大约 200/20= 10 kWh/每人天，大约是典型欧盟公民能源预算的 10%。总而言之，这还不错，但也不是解决能源危机的方法。
 
The easiest target for increasing this number is to simply build more windmills, but that likely requires going offshore (higher wind speeds, more real estate), which means rapid deterioration due to rust, seawater, etc. and thus more energy going into producing windmills in the first place. Therefore, wind power will likely supplement our overall energy budget.
增加这个数字最简单的目标是简单地建造更多的风车，但这可能需要去海上（更高的风速，更多的空间），这意味着由于生锈、海水等原因而迅速恶化，因此首先要有更多的能源用于生产风车。因此，风力发电可能会补充我们的整体能源预算。

Solar Power 太阳能

Now let’s consider solar power. The calculation is a good deal simpler than that for wind. The intensity of solar radiation at the distance of the Earth is about $1300{\text{ W/m}}^2$. Averaging over the entirety of the Earth, and accounting for the effective cross section, this turns into about $300{\text{ W/m}}^2$ for the average parcel of land on Earth.
现在让我们考虑一下太阳能。计算比风的计算简单得多。太阳辐射强度在地球的距离约为 $1300{\text{ W/m}}^2$。在整个地球上平均，并考虑有效横截面，这变成了大约 $300{\text{ W/m}}^2$ 对于地球上的平均土地。
 
Taking into account the amount of energy that’s bounced off the top of the atmosphere back into space (∼70%), and also the amount bounced off the Earth’s surface back into space (another∼70%), this gets us to roughly $10\%$ the solar radiation, or $100{\text{ W/m}}^2$.
考虑到从大气层顶部反弹回太空的能量 （∼70%），以及从地球表面反弹回太空的量（其他∼70%），这让我们得到了大约 10% 的太阳辐射，或者 $100{\text{ W/m}}^2$ .
 >

Let’s again take the E.U. as our test land mass. Top of the line solar panels can reach efficiencies of $\sim 25$, meaning that we can expect $25{\text{ W/m}}^2$. Given a population density of $5\times 10^8\text{ people}/4.5\times 10^6{\text{ km}}^2$, this figures to about $5400\text{ kWh}$ per person per day.
让我们再次将欧盟作为我们的试验地块。顶级太阳能电池板可以达到 ∼25%，这意味着我们可以预期 $25{\text{ W/m}}^2$ 。假设人口密度为 $5\times 10^8\text{ people}/4.5\times 10^6{\text{ km}}^2$，这个数字大约是每人每天 5400 kWh。
 
Adjusting down the usable land to just 5% of the land mass, we have $\sim 240\text{ kWh}$ per person per day, which could more than account for the average E.U. citizen’s daily energy usage
将可用土地调整到仅占陆地面积的 5%，我们有每人每天 240 kWh，这可能超过欧盟公民的平均每日能源使用量。

See also

Dimensional analysis.

Cite as:

Fermi Estimate. Retrieved 08:52, September 29, 2024, from https://brilliant.org/wiki/fermi-estimate/

---

数据分析中最好用的估算法：费米思想

作者 李启方

在很多数据分析面试中，主考官都喜欢问应试者这样的一些问题：

“不用任何公开参考资料，估算今年新生儿的出生数量？”

“估算你所在的城市，每年收集到的家庭垃圾的总重量是多少？”

“估算此时此刻的世界上，有多少人正在挖鼻孔？”

…

像这种看似无厘头的问题，却常常在数据分析的面试中见到，而如果应试者没有一定的数据思维，第一反应一定是：

“你疯了吧？这种问题我怎么回答？”

如果你这么回答，或者是胡乱猜一个数字，那么恭喜你，你可以去准备下一场面试了。

其实这样的题目看似无法回答，但实际上主考官考验的是你的数据思维能力，如何在数据不明确、以及各种限制条件下，利用一些假设的理由和经验推算出正确答案。

这也就涉及到了我们要分享的数据分析思想 ——费米问题。

一、神奇的费米问题

费米是意大利裔的美国物理学家，曾在 1938 年获得诺贝尔物理学奖，而他被世人所更为熟知的，则是他在芝加哥大学课堂上凭空抛出的一个看似荒谬的问题：

“芝加哥有多少个钢琴调音师？”

听到这个问题的学生都是一脸茫然，费米则提示遇到这样看似庞大的问题，可以把这个问题分解成一些便于操作和认知的小问题，根据猜测和假设去估算问题。

这也就是费米问题思想的核心：逻辑拆解。

也就是说把一个庞大的、抽象的、复杂的问题，逐级拆解为微小的、具体的、简单的问题，然后再将这些小问题进一步拆解，只要保证了逻辑关系，那么将这些可以回答的小问题答案，逐步反推到费米问题上，就可以得到最终的准确答案。

在麦肯锡分析思维中，这种方法叫做 “逻辑树法”。

现在我们再回过头来，看一下费米是怎么解答的呢？

首先费米将这个问题拆解成了两个问题：每年芝加哥全部调音师的工作时长，以及一位调音师每年的工作时间。

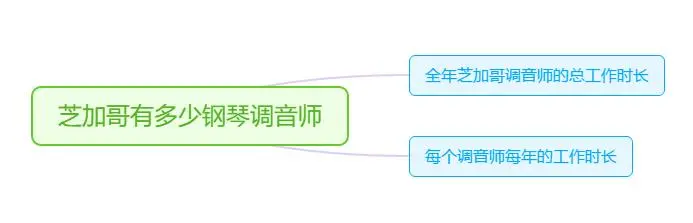
为什么要拆解成这两个问题呢？因为我们在拆解问题的时候需要按照一定的逻辑关系，这个逻辑关系必须要保证能够完全覆盖费米问题的所有范围。

比如这个问题的拆解逻辑是：

总人数 = 总时长 / 单个时长

然后我们再先看一下，每年芝加哥全部调音师的工作时长是多少？费米继续将这个问题进行拆解，拆解为了 3 个问题：

• 芝加哥有多少架钢琴？
• 每架钢琴多久调一次音？
• 一位调音师的调音时长？

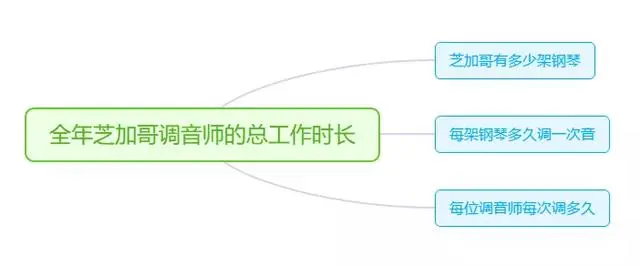
拆解逻辑是：

钢琴数 * 每年调音次数 * 调音时长 = 每年总调音时长

现在问题又变成了芝加哥有多少钢琴和每年调音的次数，这样的问题还能继续拆解吗？

答案是不能，这样的问题就属于费米问题的基本问题，基本问题的确定就要涉及费米问题的另一个主要思想：问题估算。

二、天才的大数估算法

对于基本问题的估算方法，费米给出了一个天才式的估算方法：

对于小问题的估算，不要估算其本身，而是先估算其上下界，然后在 10 倍的范围内估算出数值，这种方法竟然能保证极高的准确率。

至于原因，我们稍后再讲，先看一下费米是怎么估算的。

首先是如何知道芝加哥的钢琴数，费米先估算了芝加哥总居民数是 300 万（这个不用估算也基本能知道），平均每个家庭有 4 个人（美国四人家庭居多），那么芝加哥估计会有 75 万个家庭。

这些家庭中有多少有钢琴呢？在当时的美国，钢琴属于半稀缺物品，拥有钢琴的家庭应该不会超过 1/2，也不会低于 1/10，因此费米估算为 1/3，那么全市大概会有 25 万架钢琴。

第二个基本问题是每架钢琴每年需要调音几次，调音师不是常见的岗位，调音次数应该不会超过 1 年 3 次，也不会低于 10 年 1 次，因此费米估算为 3 年 1 次，也就是每年 0.33 次，那么每年全市有 8.3 万架钢琴需要调音。

第三个基本问题是调音一次要花多久，不会超过 10 小时，也不会低于 1 小时，因此费米估算为 3 小时。

这样第一个大问题我们就解决了，总钢琴的总调音时长大约是 3*83000=249000

下面估算第二个大问题：每年每位调音师工作多久？

假设调音师一年工作 250 天，算上他每天需要往返的路时，那么他一年的工作时间就是 250240.6=3600H

这样所有的问题都已经估算出了结果，最终调音师数量 = 249000/3600=69 位

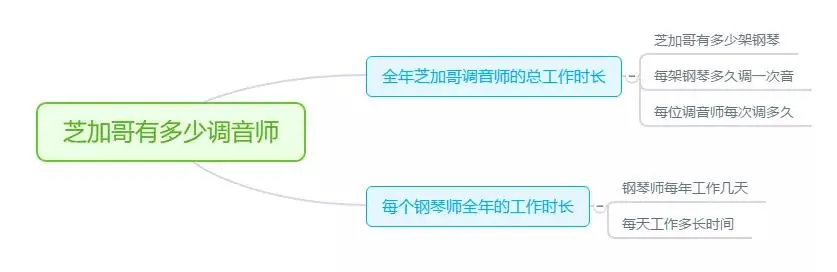
那么实际上有多少人呢？经过费米和学生们事后进行电话号码验证，大概芝加哥市有 80 位调音师，除去一些号码重复的，其结果竟然跟费米估算的相差无几！

三、暗中帮助的平均律

但是可能有人会产生质疑，如果将费米估算中家庭拥有钢琴率改为 1/5，而不是 1/3，其结果不就会改变了吗？费米的这些估算难道都是巧合吗？

其实，费米估算法中涉及到了一个数据概念：平均律。

他的原理是在任何一组计算中，估算带来的错误都可以相互抵消，所做的假设越多，被抵消的概率就会越大。

也就是说，有人会假设 1/5 的家庭拥有钢琴，他也可能同时会假设每架钢琴需要 1 年调 1 次音，而不是 3 年调一次，这样一高一低，错误估计就会被相互抵消。

换成数据分析的语言就是，你在假设或者猜测某一个小事件的时候，你的推测假设有可能有的过高，有可能有的过低，如果这些 “点” 的数量足够，最终误差就会被相互抵消，整体结果最终会呈现为一个平均值，这就是平均律理论。

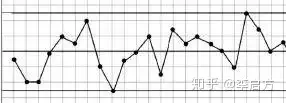
其实就类似于上图，我们确定一个估算上边界，以及一个估算下边界，所有落在这个范围里面的点都会趋向于平均值，落在平均值上的点和平均值下的点就会相互抵消消除，其结果也就趋于一个准确值了。

这也就是为什么费米估算法会百试百灵，准确率十分之高了！

四、费米思想如何用在数据分析中

费米估算法求出的是一种数量级上的准确，这种准确是由一些要素保证的，首先是模型的准确性，这是基础，无论是物理定律还是生活经验都要经受住检验；

其次是变量估计的准确，这个很好理解，你对这个变量越不确定，答案就有可能越不靠谱；

第三条很重要，是对第二条的补救，对一个变量组，每个变量都选择可能性最大的值，最后会在概率意义上得到很好的结果（通俗地说，有可能估计大也可能估计小了，但是最后抵消了，所以参数越多，稳定性越好）。

所以说，费米处理问题的方式是将复杂、困难的问题分解成小的、可以解决的部分，从而以最直接的方法迅速解决问题。这种思维方式非常实用，可以帮助我们解决很多日常甚至重要的问题。

在实际生活中，我们常常需要在信息不全的情况下做出判断决策，要使我们的决定尽可能正确，最有效的策略就是 “费米思维”。

最后给大家分享老李常用的数据分析工具和分析报告模板：

免费试用 BI 工具 FineBIwww.fanruan.com/actionform?action=active-fbi

发布于 2020-03-10 17:26・IP 属地江苏 ，编辑于 2023-10-16 17:12・IP 属地江苏

---

费米估算 | 产品面试中的估算问题解法

作者 苏 Eddie 2020-05-30

费米估算可以解决产品面试中的估算问题。本文介绍了费米估算的起源、原理、方法和案例！

前言：前段时间在分析大厂产品面试题，发现估算题目出现的概率蛮大。比如估算北京一年出租出去的房子数量，估算一个城市的加油站等，这类问题（Market Sizing）貌似没有已知条件。

查找相关资料后，才知道费米给出了一套解决这类问题的方法论。

费米问题的本质在于将未知问题逐步拆解成已知问题，通过建模和生活经验给出毛估。这篇文章会介绍下费米估算和如何解决这类 Market Sizing 估算问题。

一、费米估算：起源

有这样的一个故事：

在一次芝加哥大学课堂上，费米问学生。芝加哥市有多少调琴师，学生们一脸茫然。费米提示把这个问题 “分解成一些便于操作的小问题，然后鼓起勇气作猜测和假设”。

芝加哥有多少居民？可靠的估算是 300 万；平均每个家庭有多少人？4 人；多少家庭有钢琴？大概三分之一，那么全市大约就有 25 万架钢琴；一架钢琴隔多长时间需要调音？平均 5 年，那么芝加哥平均每年有 5 万架次的钢琴需要调音；每个调音师每天能为多少架钢琴调音？4 架；假设他一年工作 250 天，那么他每年约为 1000 架钢琴调音。

由此，费米和学生们推测，芝加哥市大概有 50 位钢琴调音师。

事后有人用电话号码簿加以验证，实际统计的结果与费米的猜测十分接近。

二、费米估算的原理

1. 费米估算的概念

费米估算指的是解决未知结果的估算问题，将复杂的问题拆解成小的、可知结果的部分。

将拆解出来的简单部分赋予实际意义，如果还不能得出结果，那就继续再拆解，直到拆解后的所有部分问题变成一个常识问题或者是比较容易解决的，从而将一个未知结果的问题逐步变得清晰。

2. 平均律

在将复杂的问题拆解成小的、可知结果的部分过程中，可能会存在估算，那么这样的估算会不会给最终结果带来很大的误差呢？

比如前面例子中，费米估算芝加哥有 1/3 家庭有钢琴，如果当时估算的是 1/4，那结果就会不准确了吗？

其实在费米估算过程中，我们不是只有一次估算，我们会产生一系列的估算。比如估算芝加哥有 1/3 家庭有钢琴，同时也会估算一架钢琴平均 5 年调一次音。这些估算有的过高有的过低，相乘之后会相互抵消，回归到较为准确的平均值。

费米估算不是万能的，有个很重要的前提，我们的估算值是有实际数据或者生活经验支撑的。估算值不能偏离实际结果太远，要从实际结果、常识出发。比如费米在估算芝加哥每个家庭有 4 个人，换成我们来估算的话，我们不能拍脑袋直接估算芝加哥每个家庭有 10 个人。

这种脱离实际常识、数据的估算其实是瞎猜，瞎猜怎么能对呢？

三、如何用费米估算 Market Sizing 问题

最近在分析些产品面试题，发现一些大厂喜欢出这样的估算题目，比如：

估算杭州每年奶茶店的规模大小？

估算杭州一家奶茶店一天卖多少杯奶茶？

估算杭州有多少家奶茶店？

这类问题称为 Market Sizing 问题，有些同学在面试时碰到这类问题，如果没有提前了解这类题型，难以找到比较好的回答思路。

这类 Market Sizing 题型正好可以通过费米估算的法则来解决，将未知的数逐步拆解成已知的部分，从而将一个未知结果的问题逐步变得清晰。

Market Sizing 问题在运用费米估算时，主要是通过需求端、供给端两个角度切入将问题拆解。这两个角度可以解决 80% 的 Market Sizing 问题，当然有些不涉及商品的规模、数量的问题，这两个角度可能解决不了。

那就需要对这个问题进行数学分析，列出公式，从而拆解。

费米估算步骤：

• 明确问题
• 分析是需求端问题还是供给端问题，或者两个角度都不是
• 问题拆解，列公式
• 计算

对问题进行拆解时，我们提倡按照不重不漏（MECE，Mutually Exclusive Collectively Exhausted）的原则 ，将问题层层拆解成子问题，从而找到问题的根源。

在对问题进行拆解的时候，我们需要注意两个问题。

1）避免把未知数拆解成新的未知数，而应该使得拆解后的元素变得可解决

举个例子，在 “估算杭州一家奶茶店一天卖多少杯奶茶？” 中，我们从需求端出发，先是估算杭州常住人口为 1000 万，接着估算

每天喝奶茶的人 = 常住人口 * 渗透率

假设渗透率是 1%，估出每天喝奶茶的人是 10 万，每人每天喝一杯。然后估算杭州有 1000 家奶茶店，最终得出每家奶茶店一天卖 100 杯奶茶。

问题来了，我们刚刚拆解杭州奶茶店这个元素，我们估算是 1000 家，其实这是个特别关键的值。这个值直接影响到了每家奶茶店平均卖多少杯奶茶。但杭州有多少家奶茶店这个值其实也是个未知数（并不能通过常识或者数据得知，别跟我说去百度一下）。从一个未知数继续推出一系列未知数，这样

所以拆解后的元素不能还是未知数，如果还是未知数则需要继续拆解，使得拆解后的元素变得可解决。

2）对拆解后的部分赋予数值时，避免改变数值真实范围

不改变数值真实范围指的是在赋予计算公式中各元素以实际意义的时候，不扩大或者缩小范围，按照数据或者经验来赋予较为准确的范围。

前文也谈论到，比如费米在估算芝加哥每个家庭有 4 个人，换成我们来估算的话，我们不能拍脑袋直接估算芝加哥每个家庭有 10 个人。我们的估算值应该是有实际数据或者生活经验支撑的。

在面试的时候碰到这类估算问题，千万别直接说可以百度查找等这类回答，或者转牛角尖死磕某一数据的准确性。

面试官通过这类题目考察的其实是面试者的分析方法和逻辑，对于问题拆解的边界考虑，答案可能并不是那么重要，这个思考过程才是面试官想要的。

四、案例分析

1. 估算杭州每年奶茶店的规模大小？

4.1.1 明确问题

Q：问的是杭州每年奶茶店的规模大小，规模大小具体指的是什么？

A：规模大小指的是奶茶店的销售额大小

Q：奶茶店的销售额是指仅仅销售奶茶的收入，还是包括奶茶店里别的饮料和面包等食品？

A：奶茶店的销售额指的是所有饮品（不统计面包这类食品）

4.1.2 分析需求端问题还是供给端问题，或者两个角度都不是

这个问题问的是杭州每年奶茶店的规模，是一个地域的市场规模，这类问题一般可从需求端（消费者）切入，因为杭州常住人口是一个可知的数字。初步判定可从需求端出发。

4.1.3 问题拆解，列公式

杭州每年奶茶店的规模大小 = 杭州常住人口 * 渗透率 *50* 饮品单价 * 每人每周续购杯数

从需求端将未知问题拆解成元素后，我们发现：

杭州常住人口：杭州常住人口数是已知的，这属于常识，目前是 1000 万左右。

渗透率：渗透率指的是有多少比例的人会选择喝奶茶，这个比例需要我们估算。估算的时候要避免改变数值真实范围，不能估算的太离谱。

这里主要是考察边界问题，我们在回答的时候可以说通过样本估算。比如我随机选择 100 位朋友，看 100 位朋友中有多少人是符合条件的，从而估算出渗透率。

这里还有一个关键问题，不同年龄段的人喝奶茶的频率是不一样的。根据生活经验，年轻人喝奶茶次数会比中年人喝老年人高，所以我们可以通过 MECE 法则将杭州常住人口分为小孩、年轻人、中年人和老年人，计算公式依然没有变，最终相加各类型的规模大小即可。

• 每人每周续购杯数：解决办法同上。
• 52：指的是一年约有 52 周，是已知数。
• 饮品单价：根据我们的生活常识，蜜雪冰城的奶茶均价 8 元，喜茶的奶茶均价在 30 元一杯。所以饮品单价我们可取 15 元一杯。

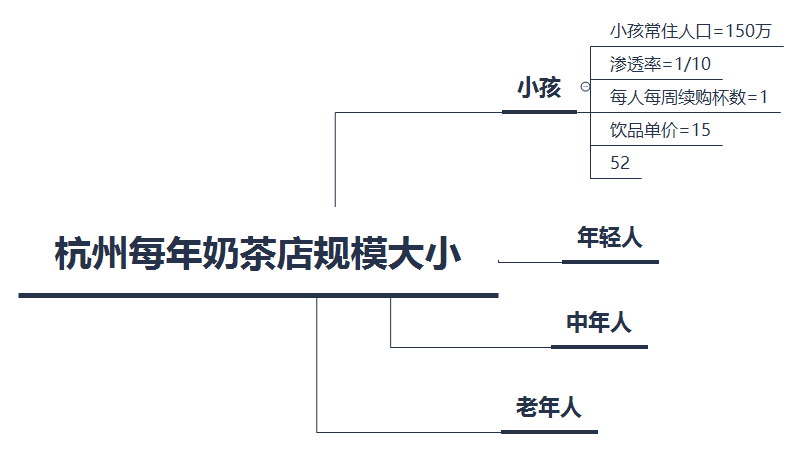
4.1.4 计算

杭州每年奶茶店规模大小 =（1500.115152）+（3000.4151.552）+（4000.1150.552）+（1500.05150.552)=170625 万

估算出杭州每年奶茶店的规模大小约为 17 亿。

2. 估算杭州一家奶茶店一天卖多少杯奶茶

4.2.1 明确问题

Q：奶茶指的是店里所有饮品？

A：是的

4.2.2 分析需求端问题还是供给端问题，或者两个角度都不是

这个问题如果也从需求端出发，会发现很难拆解出有意义的元素，因为店里的顾客人流是不确定。所以一般这种要从供给端出发，看奶茶店能提供多少杯奶茶。因为一般情况下，供给需求是平衡的。

4.2.3 问题拆解，列公式

杭州一家奶茶店一天卖出奶茶杯数 = 工作时长 * 一窗口每小时卖出多少杯 * 售卖窗口

从供给端将未知问题拆解成元素后，我们发现：

• 工作时长：早上 9 点到晚上 9 点，一共 12 小时，已知数。
• 一窗口每小时卖出多少杯：以天为单位，存在高峰和低峰期。根据生活经验，估算高峰期为 12-14 点和 18-21 点，低峰期为 9-12 点和 14-18 点。同时根据生活经验，制作一杯奶茶需要 3 分钟，高峰期一窗口每小时卖出 15 杯，低峰期一窗口每小时卖出 5 杯。
• 售卖窗口：预估一个奶茶店有售卖窗口（制作机器）有 3 个。

4.2.4 计算

杭州一家奶茶店一天卖多少杯奶茶 =（5153）+（753）=330

估算出杭州一家奶茶店一天能卖 330 杯奶茶。

五、总结

面试的时候碰上这类问题，可以从上面总结的四个步骤来分析：

1. 明确问题
2. 分析是需求端问题还是供给端问题，或者两个角度都不是
3. 问题拆解，列公式
4. 计算

面试官考察点不会是我们最终的答案准不准确，而是看我们对问题进行拆解时合不合理，看我们能不能对我们的估算给出合理的解释。这类题型不必太在意细节和纠结于数字的精准度。

当然啦，如果是面试时第一次碰到这类问题还是很难快速找到思路，所以日常的时候可以刻意分析下这类题型，学会费米估算对我们来说受益匪浅。

费米估算在极其有限的条件下，通过拆解未知并利用身边的信息来求解出结果。

费米估算也给到了我一些启发，即便有些事情看上去无法确定，但可以通过分析拆解，逐步逼近结果。面对不确定性，我们不应停滞不前，而是要懂得抓住身边有价值信息，快速决策。

---

via：

• 数据分析中最好用的估算法：费米思想 - 知乎 编辑于 2023-10-16 17:12・IP 属地江苏
  https://zhuanlan.zhihu.com/p/112238260

• 费米估算 | 产品面试中的估算问题解法 | 人人都是产品经理 作者：苏 Eddie
  https://www.woshipm.com/pmd/3941089.html