数据压缩基本原理及常用算法 | 无损压缩历史_数据压缩基础理论-优快云博客

本文链接：https://blog.youkuaiyun.com/u013669912/article/details/142322751

注：机翻，未校。

Fundamentals of Compression

数据压缩基本原理

Friday, December 26th, 2014

Compression is the process of reducing the storage space requirement for a set of data by converting it into a more compact form than its original format. This concept of data compression is fairly old, dating at least as far back as the mid 19th century, with the invention of Morse Code.

Morse Code was created to enable operators to transmit textual messages across an electrical telegraph system using a sequence of audible pulses to convey characters of the alphabet. The inventors of the code recognized that some letters of the alphabet are used more frequently than others (e.g. E is much more common than X), and therefore decided to use shorter pulse sequences for more common characters and longer sequences for less common ones. This basic compression scheme provided a dramatic improvement to the system’s overall efficiency because it enabled operators to transmit a greater number of messages in a much shorter span of time.

Although modern compression processes are significantly more complicated than Morse Code, they still rely on the same basic set of concepts, which we will review in this article. These concepts are essential to the efficient operation of our modern computerized world — everything from local and cloud storage to data streaming over the Internet relies heavily on compression and would likely be cost ineffective without it.
压缩是通过将一组数据转换为比其原始格式更紧凑的形式来减少一组数据的存储空间要求的过程。这种数据压缩的概念相当古老，至少可以追溯到 19 世纪中叶，当时摩斯电码的发明。摩尔斯电码的创建是为了使操作员能够使用一系列可听脉冲通过电报系统传输文本消息，以传达字母表中的字符。该代码的发明者认识到字母表中的某些字母比其他字母使用得更频繁（例如 E 比 X 更常见），因此决定对更常见的字符使用较短的脉冲序列，对不太常见的字符使用较长的序列。这种基本的压缩方案极大地提高了系统的整体效率，因为它使操作员能够在更短的时间内传输更多的消息。尽管现代压缩过程比摩尔斯电码复杂得多，但它们仍然依赖于相同的基本概念集，我们将在本文中对其进行回顾。这些概念对于我们现代计算机化世界的高效运行至关重要——从本地和云存储到互联网上的数据流，一切都严重依赖压缩，如果没有压缩，可能会成本效益低下。

Compression Pipeline 压缩管道

The following figure depicts the general paradigm of a compression scheme. Raw input data consists of a sequence of symbols that we wish to compress, or reduce in size. These symbols are encoded by the compressor, and the result is coded data. Note that although the coded data is usually smaller than the raw input data, this is not always the case (as we’ll see later).
下图描述了压缩方案的一般范例。原始输入数据由我们希望压缩或缩小大小的符号序列组成。这些符号由 Compressor 编码，结果是编码数据。请注意，尽管编码数据通常小于原始输入数据，但情况并非总是如此（我们稍后将看到）。

Coded data may then be fed into a decompressor, usually at a later point in time, where it is decoded and reconstructed back into raw data in the form of an output sequence of symbols. Note that throughout this article we’ll use the terms sequence and string interchangably to refer to a sequential set of symbols.

If the output data is always identical to the input, then the compression scheme is said to be lossless, and utilizes a lossless encoder. Otherwise, it is a lossy compression scheme.

Lossless compression schemes are usually employed for compression of text, executable programs, or any other type of content where identical reconstruction is required. Lossy compression schemes are useful for images, audio, video, or any content where some degree of information loss is acceptable in order to gain improved compression efficiency.

然后，编码数据可以被馈送到解压缩器中，通常在稍后的某个时间点，在那里它被解码并以输出符号序列的形式重建回原始数据。请注意，在本文中，我们将交替使用术语 sequence 和 string 来指代一组连续的符号。如果输出数据始终与输入相同，则称为压缩方案是无损的，并使用无损编码器。否则，它是一个有损压缩方案。无损压缩方案通常用于压缩文本、可执行程序或需要相同重建的任何其他类型的内容。有损压缩方案适用于图像、音频、视频或可接受一定程度信息丢失的任何内容，以便提高压缩效率。

Data Modelling 数据建模

Information is defined as a quantity that measures the complexity of a piece of data. The more information that a data set has, the harder it is to compress it. The notion of rarity is correlated with this concept of information because the occurrence of a rare symbol provides more information than the occurrence of a common one.

For example, the occurrence of an earthquake in Japan would provide less information than an earthquake on the moon, as earthquakes are far less common on the moon. We can expect most compression algorithms to carefully regard the frequency or probability of a symbol when deciding how to compress it.

We describe the efficiency of a compression algorithm as its effectiveness at reducing information load. A more efficient compression algorithm will reduce the size of a particular data set more than a less efficient algorithm.
信息被定义为衡量一段数据复杂性的数量。数据集包含的信息越多，压缩它就越困难。稀有性的概念与这个信息概念相关，因为稀有符号的出现比常见符号的出现提供的信息更多。例如，日本发生地震提供的信息比月球上的地震少，因为地震在月球上的情况要少得多。我们可以预期大多数压缩算法在决定如何压缩品种时会仔细考虑品种的频率或概率。我们将压缩算法的效率描述为它在减少信息负载方面的有效性。与效率较低的算法相比，更高效的压缩算法将更能减小特定数据集的大小。

Probability Models 概率模型

One of the most important steps in designing a compression scheme is to create a probability model for the data. This model allows us to examine the characteristics of the data in order to efficiently fit a compression algorithm to it. Let’s walk through part of the modelling process to make this a bit more clear.
设计压缩方案的最重要步骤之一是为数据创建概率模型。该模型允许我们检查数据的特征，以便有效地将压缩算法拟合到它。让我们来了解一下建模过程的一部分，以使其更加清晰。

Let’s assume we have an alphabet, G, which consists of all possible symbols in a data set. In our example, G contains precisely four symbols: A through D.
假设我们有一个字母表 G，它由数据集中所有可能的符号组成。在我们的示例中，G 恰好包含四个符号：A 到 D。

$G=\langle A,B,C,D\rangle$

We also have a probability density function, P, which defines the probabilities for each symbol in G actually occurring in an input string. Symbols with higher probabilities are more likely to occur in an input string than symbols with lower probabilities.
我们还有一个概率密度函数 P，它定义了 G 中每个符号在输入字符串中实际出现的概率。概率较高的符号比概率较低的符号更有可能出现在输入字符串中。

$P(A)=0.2\text{ }P(C)=0.1$

$P(B)=0.4\text{ }P(D)=0.3$

For this example we will assume that our symbols are independent and identically distributed. The presence of one symbol in a source string is expected to have no correlation to the presence of any other.
对于此示例，我们将假设我们的品种是独立的并且分布相同。源字符串中存在一个符号应与任何其他符号的存在无关。

Minimum Coding Rate 最小编码速率

B is our most common symbol, with a probability of 40%, while C is our least likely symbol, which occurs only 10% of the time. Our goal will be to devise a compression scheme that minimizes the required storage space for our common symbols, while supporting an increase in the necessary storage space for more rare symbols. This trade off is a fundamental principle of compression, and inherint in virtually all compression algorithms.
B 是我们最常见的符号，概率为 40%，而 C 是我们最不可能的符号，只出现 10% 的时间。我们的目标是设计一种压缩方案，以最小化我们的常见符号所需的存储空间，同时支持增加更多稀有符号所需的存储空间。这种权衡是压缩的基本原则，几乎是所有压缩算法中固有的。

Armed with the alphabet and pdf, we can take an initial shot at defining a basic compression scheme. If we simply encoded symbols as raw 8 bit ASCII values, then our compression efficiency, known as the coding rate, would be 8 bits per symbol. Suppose we improve this scheme by recognizing that our alphabet contains only 4 symbols. If we dedicate 2 bits for each symbol, we will still be able to fully reconstruct a coded string, but require only 1/4th the amount of space.

At this point we have significantly improved our coding rate (from 8 to 2 bits per symbol), but have completely ignored our probability model. As previously suggested, we can likely improve our coding efficiency by incorporating our model, and devising a strategy that dedicates fewer bits to the more common symbols (B and D), and more bits to the less common symbols (A and C).

This brings up an important insight first described in Shannon’s seminal paper — we can define the theoretical minimum required storage space for a symbol (or event) based simply on its probability. We define the minimum coding rate for a symbol as follows:
有了 alphabet 和 pdf，我们可以初步定义一个基本的压缩方案。如果我们简单地将符号编码为原始的 8 位 ASCII 值，那么我们的压缩效率（称为编码速率）将是每个符号 8 位。假设我们通过认识到我们的字母表只包含 4 个符号来改进这个方案。如果我们为每个符号专用 2 位，我们仍然能够完全重建一个编码字符串，但只需要 1/4 的空间。在这一点上，我们已经显著提高了编码速率（每个符号从 8 位提高到 2 位），但完全忽略了我们的概率模型。如前所述，我们可以通过合并我们的模型，并设计一种策略来提高编码效率，将更少的位专用于更常见的符号（B 和 D），而将更多的位专用于不太常见的符号（A 和 C）。这带来了一个重要的见解，该见解在 Shannon 的开创性论文中首次描述——我们可以简单地根据其概率来定义品种（或事件）的理论最小所需存储空间。我们定义交易品种的最小编码速率如下：

$MCR(S)=-{{\log }_{2}}(P(S))$

For example, if a symbol occurs 50% of the time, then it would require, at an absolute minimum, 1 bit to store it.
例如，如果一个 symbol 在 50% 的时间内出现，那么它绝对至少需要 1 bit 来存储它。

Entropy and Redundancy 熵和冗余

Going further, if we compute a weighted average of the minimum coding rates for the symbols in our alphabet, we arrive at a value that is known as the Shannon entropy, or simply the entropy of the model. Entropy is defined as the minimum coding rate at which a given model may be coded. It is based on an alphabet and its probability model, as described below.
更进一步，如果我们计算字母表中符号的最小编码率的加权平均值，我们会得到一个称为香农熵的值，或者简称为模型的熵。熵定义为可以对给定模型进行编码的最小编码速率。它基于字母表及其概率模型，如下所述。

$H(G,P)=-\sum\limits_{i=0}^{n}{P({{X}_{i}}){{\log }_{2}}(P({{X}_{i}}))}$

$\text{for }{{\text{X}}_{\text{i}}}\in G$

As one might expect, models with many rare symbols will have a higher entropy than models with fewer and more common symbols. Furthermore, models with higher entropy values will be harder to compress than those with lower entropy values.
正如人们所料，具有许多稀有符号的模型将比具有较少和更多常见符号的模型具有更高的熵。此外，具有较高熵值的模型将比具有较低熵值的模型更难压缩。

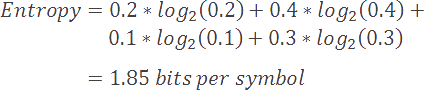
In our current example, our model has an entropy of 1.85 bits per symbol. The difference between our current coding rate (2) and entropy (1.85) is known as the redundancy of our compression scheme.
在我们当前的例子中，我们的模型每个符号的熵为 1.85 位。我们当前的编码率（2）和熵（1.85）之间的差异称为压缩方案的冗余。

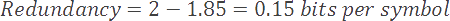
Entropy is an extremely useful topic with applicability to many different subfields including encryption and artificial intelligence. A full discussion of entropy is outside the scope of this article, but interested readers can learn much more here.

熵是一个非常有用的主题，适用于许多不同的子领域，包括加密和人工智能。对熵的全面讨论不在本文的范围之内，但感兴趣的读者可以在这里了解更多信息。

Coding the Model 对模型进行编码

We’ve taken a slight liberty thus far, and have automatically given ourselves the probabilities of our symbols. In reality, the model may not always be readily available and we will need to derive these values either through analysis of source strings (e.g. by tallying symbol probabilities from exemplar data), or by adaptively learning the model in tandem with a compression process. In either case, the probabilities of the actual source data may not perfectly match the model, and we will lose efficiency proportional to this divergence. For this reason, it is important to derive (or constantly maintain) as accurate a model as possible.
到目前为止，我们稍微放纵了一下，并自动地给了自己我们品种的概率。在现实中，该模型可能并不总是容易获得，我们需要通过分析源字符串（例如，通过计算示例数据的符号概率）或通过自适应地学习模型与压缩过程来推导出这些值。在任何一种情况下，实际源数据的概率都可能与模型不完全匹配，我们将损失与这种差异成正比的效率。因此，得出（或持续维护）尽可能准确的模型非常重要。

Common Algorithms 常用算法

Once the probability model is defined for a set of data, we are able to devise a compression scheme that properly leverages the model. While the process of developing a new compression algorithm is beyond the scope of this article, we can leverage existing algorithms to fit our needs. We review some of the most popular algorithms below.

Each of the following algorithms is a sequential processor, which means that in order to reconstruct the nth element from a coded sequence, the previous 0…(n-1) symbols must first be decoded. Seeking operations are not possible because of the variable length nature of the encoded data — the decoder has no way of jumping to the correct offset for symbol n without first decoding all previous symbols. Additionally, some coding schemes rely on internal historical state that is maintained only by processing each symbol within a sequence in order.
一旦为一组数据定义了概率模型，我们就能够设计出一个压缩方案来适当地利用该模型。虽然开发新压缩算法的过程超出了本文的范围，但我们可以利用现有算法来满足我们的需求。我们在下面回顾了一些最流行的算法。以下每种算法都是一个顺序处理器，这意味着为了从编码序列中重建第 n 个元素，之前的 0…（n-1）符号必须首先解码。由于编码数据的长度可变性，因此无法进行搜索操作 — 如果不先解码所有先前的符号，解码器就无法跳转到符号 n 的正确偏移量。此外，某些编码方案依赖于内部历史状态，该状态仅通过按顺序处理序列中的每个元件来维护。

- Huffman Coding 霍夫曼编码

This is one of the most well known compression schemes and it dates back to the early 1950s, when David Huffman first described it in his paper, “A Method for the Construction of Minimum Redundancy Codes.” Huffman coding works by deriving an optimal prefix code for a given alphabet.

A prefix code ascribes a numerical value to each symbol in an alphabet such that no symbol’s code is a prefix for any other symbol’s code. For example, if 0 is the code for our first symbol, A, then no other symbol in our alphabet may begin with a 0. Prefix codes are useful because they enable precise and unambiguous decoding of a bit stream.
霍夫曼编码这是最著名的压缩方案之一，它可以追溯到 1950 年代初，当时 David Huffman 在他的论文“A Method for the Construction of Minimum Redundancy codes”中首次描述了它。霍夫曼编码的工作原理是为给定字母表派生最佳前缀代码。前缀代码为字母中的每个符号赋予一个数值，这样，任何符号的代码都不会是任何其他符号代码的前缀。例如，如果 0 是我们的第一个符号 A 的代码，那么字母表中的其他符号都不能以 0 开头。前缀代码很有用，因为它们支持精确和明确的 bit stream 解码。

The process for deriving an optimal prefix code for a given alphabet (the essence of Huffman coding) is outside the scope of this article, but check out my other blog post that describes the process in detail.
为给定字母表派生最佳前缀代码的过程（霍夫曼编码的精髓）不在本文的讨论范围之内，但请查看我的另一篇博客文章，其中详细描述了该过程。

The following table illustrates the Huffman codes for all symbols in our alphabet.
下表说明了我们字母表中所有符号的霍夫曼码。

Symbol	Probability	Code
B	0.4	0
D	0.3	10
A	0.2	110
C	0.1	111

Now, let’s examine the effectiveness of a sample prefix code for our example alphabet, G. Notice that we’ve assigned shorter codes to more common symbols, and longer codes to less common ones.
现在，让我们检查一下示例字母表 G 的示例前缀代码的有效性。请注意，我们已将较短的代码分配给更常见的符号，而将较长的代码分配给不太常见的符号。

Using this system, our average coding rate is significantly reduced to 1.9 bits per symbol, versus our previous best value of 2, and our redundancy is reduced to 0.05 bits per symbol (versus 0.15).
使用这个系统，我们的平均编码速率显著降低到每个符号 1.9 位，而我们之前的最佳值为 2，我们的冗余降低到每个符号 0.05 位（而不是 0.15）。

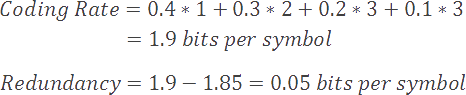
- Dictionary Approaches 字典法

Coders of this type leverage a dictionary to store recently observed symbols. When a symbol is encountered, it is first checked against the dictionary, to see if it is already stored. If it is, then the output will simply consist of a reference to the dictionary entry (usually an offset), rather than the full symbol.

Examples of common dictionary based compression schemes include LZ77 and LZ78, which serve as the foundation for many different lossless encoding schemes.

In some cases, a sliding window is used to adaptively track recently seen symbols. In these cases, a symbol is only maintained in the dictionary if it has been seen relatively recently. Otherwise, the symbol is evicted (and potentially re-entered for a later occurrence). This process prevents symbol indices from growing too large, and leverages the fact that symbols in a sequence may recur within a relatively short window.
字典方法这种类型的编码人员利用字典来存储最近观察到的符号。当遇到一个品种时，首先根据字典检查它，看看它是否已经被存储。如果是，则输出将仅包含对字典条目的引用（通常是偏移量），而不是完整的符号。常见的基于字典的压缩方案的示例包括 LZ77 和 LZ78，它们是许多不同的无损编码方案的基础。在某些情况下，滑动窗口用于自适应地跟踪最近看到的符号。在这些情况下，只有当某个符号最近出现时，才会在字典中保留该符号。否则，将逐出该符号（并可能重新输入以供以后使用）。此过程可防止 symbol indices 增长过大，并利用 sequence 中的元件可能在相对较短的窗口内重复出现的事实。

- Exponential Golomb Coding 哥伦布指数编码

Imagine you have an alphabet consisting of integers within the range of 0 to 255, and that the probability for a symbol is related to its distance from zero. In this case, low values are the most common, and higher values are increasingly more rare.

For this scenario, an Exponential Golomb Coder might be useful. Golomb coding uses a specific prefix code that gives preference to low values at the expense of high values. The following table illustrates the first few values:
指数 Golomb 编码假设您有一个由 0 到 255 范围内的整数组成的字母表，并且一个符号的概率与它与零的距离有关。在这种情况下，低值是最常见的，而较高的值越来越少见。对于这种情况，Exponential Golomb Coder 可能很有用。Golomb 编码使用特定的前缀代码，该代码以牺牲高值为代价，优先使用低值。下表说明了前几个值：

Integer	Golomb Code
0	1
1	010
2	011
3	00100
4	00101
5	00110

The process for encoding an integer is straightforward. First, increment the integer value and count the number of bits required to store this new value. Next, subtract one from the bit count and output this number of zeroes to the output stream. Lastly, output the incremented value (computed in the first step) to the bit stream.

For example, a value of 4 would be incremented to 5, or 101 binary. This value requires 3 bits for storage, so we output 2 zeroes to the output stream, followed by our binary value of 101. The result is 00101.

Like most compression schemes, the effectiveness of Golomb coding is heavily dependent upon the specific symbols in the source sequence. Sequences containing many high values will compress much more poorly than sequences with fewer, and in some cases, a Golomb coded sequence may even be greater in size than the original input string.

For more information about this coding scheme, check out this project.
对整数进行编码的过程很简单。首先，递增整数值并计算存储此新值所需的位数。接下来，从 bit count 中减去 1，并将此数量的 0 输出到输出流。最后，将递增的值（在第一步中计算）输出到 bit stream。例如，值 4 将递增为 5 或 101 二进制。该值需要 3 位进行存储，因此我们将 2 个 0 输出到输出流，后跟我们的二进制值 101。结果为 00101。与大多数压缩方案一样，Golomb 编码的有效性在很大程度上取决于源序列中的特定符号。包含许多高值的序列比包含较少值的序列压缩得更差，在某些情况下，Golomb 编码序列甚至可能比原始输入字符串的大小更大。有关此编码方案的更多信息，请查看此项目。

- Arithmetic Coding 算术编码

Arithmetic coding is a novel compression algorithm that has recently (within the last 15 years) gained tremendous popularity, particularly for media compression. Arithmetic coders are highly efficient, computationally intensive and sequential in nature.

A common variant of arithmetic coding, called binary arithmetic coding, uses only two symbols (0 and 1) in its alphabet. This variation is particularly useful because it simplifies the design of the coder, lowers the runtime computational costs, and does not require any explicit communication between the compressor and decompressor to communicate an alphabet and model.

For more information about arithmetic coding, check out my other article, Context Adaptive Binary Arithmetic Coding.
算术编码算术编码是一种新颖的压缩算法，最近（在过去 15 年内）获得了极大的普及，尤其是对于媒体压缩。算术编码器本质上是高效的、计算密集型的和顺序的。算术编码的一种常见变体称为二进制算术编码，在其字母表中仅使用两个符号（0 和 1）。这种变化特别有用，因为它简化了编码器的设计，降低了运行时计算成本，并且不需要 compressor 和 decompressor 之间任何显式通信来传达字母表和模型。有关算术编码的更多信息，请查看我的另一篇文章 Context Adaptive Binary Arithmetic Coding。

- Run Length Encoding (RLE) 行程长度编码（RLE）

Thus far we’ve assumed that our source symbols are independent and identically distributed. Our probability model and measurements for coding rate and entropy have relied upon this fact, but what if our sequence of symbols does not satisfy this requirement?

Suppose that repetition is very likely within our sequence, and that the presence of one particular symbol strongly suggests that repeated instances of it will follow. In this case, we may choose to use another encoding scheme known as run length encoding. This technique performs well with highly repetitive symbols, and poorly when there is little repetition.
游程编码（RLE）到目前为止，我们假设我们的源符号是独立的并且分布相同。我们的概率模型以及编码率和熵的测量依赖于这一事实，但如果我们的符号序列不满足这个要求怎么办？假设在我们的序列中很可能出现重复，并且一个特定符号的存在强烈表明它将随之而来的重复实例。在这种情况下，我们可以选择使用另一种称为 run length encoding 的编码方案。这种技术在处理高度重复的元件时表现良好，而在重复很少时表现不佳。

Run length encoders anticipate stretches of repeated symbols within a string, and replace them with a pair consisting of a copy of the symbol followed by a repetition count.

For example, the sequence AABBBBBBBDDD contains repetitions of A, B, and D, and would be run length encoded as the sequence A2B7D3 to represent the fact that A is repeated twice, B seven times, and D three times. Upon reconstruction, the decoder will repeat each letter according to the repetition count specified in the string to arrive back at the original input string.

As we’ve previously mentioned, this algorithm is suitable for strings with high repetition, but notice what happens when encoding a string with minimal repetition: ABCDABCD becomes A1B1C1D1A1B1C1D1, which is far worse than the original source. Similar to most other compression algorithms, the efficiency of run length encoding is heavily dependent upon how well the source string matches the underlying model of the algorithm. In the most severe cases, run length encoding may produce a compressed result that is 2 times larger than the source input.
游程编码器可以预见字符串中重复符号的拉伸，并将它们替换为由符号副本后跟重复计数组成的一对。例如，序列 AABBBBBBBDDD 包含 A、B 和 D 的重复项，并且将编码为序列 A2B7D3 的运行长度，以表示 A 重复两次、B 重复 7 次和 D 重复 3 次的事实。重建后，解码器将根据字符串中指定的重复计数重复每个字母，以返回原始输入字符串。正如我们之前提到的，此算法适用于重复率高的字符串，但请注意在对重复率最低的字符串进行编码时会发生什么：ABCDABCD 变为 A1B1C1D1A1B1C1D1，这比原始源差得多。与大多数其他压缩算法类似，游程编码的效率在很大程度上取决于源字符串与算法底层模型的匹配程度。在最严重的情况下，游程编码可能会产生比源输入大 2 倍的压缩结果。

A Lossy Note 有损压缩

Although lossy compression is outside the scope of this article, it is important to note that lossy compression often utilizes a lossless compressor as a part of its pipeline. Lossy compression may be achieved as a two step process where data is first carefully decimated (to discard unwanted or unnecessary information), and then compressed using a lossless algorithm. Popular image and video codecs such as JPEG and H.264 do precisely this, and rely upon lossless algorithms such as Huffman encoding or arithmetic encoding to help achieve their great efficiencies.
尽管有损压缩不在本文的讨论范围之内，但重要的是要注意，有损压缩通常使用无损压缩器作为其管道的一部分。有损压缩可以作为一个两步过程来实现，其中首先小心地抽取数据（丢弃不需要或不必要的信息），然后使用无损算法进行压缩。流行的图像和视频编解码器（如 JPEG 和 H.264）正是这样做的，并依靠无损算法（如 Huffman 编码或算术编码）来帮助实现其出色的效率。

Conclusion 结论

This article has focused on lossless compression techniques and provided a brief introduction to some of the most popular techniques. Hopefully this has piqued your interest in the important field of data compression, and provided pointers for further reading on the subject.
本文重点介绍了无损压缩技术，并简要介绍了一些最流行的技术。希望这激起了您对数据压缩这一重要领域的兴趣，并为进一步阅读该主题提供了指导。

via:

Fundamentals of Compression - Bertolami.com In Compression

https://bertolami.com/index.php?engine=blog&content=posts&detail=fundamentals-of-data-compression

关于压缩（Compaction）与压缩（Compression）的区别

wanghenshui

这段内容在原文是没有的，翻译君实在没有什么好办法，不得不加上这段话
RocksDB 涉及两个压缩概念，英文原文是 Compaction 和 Compression。两个术语用中文翻译，都是 “压缩”，实际上大家交流的时候也都是使用 “压缩”。这个 wiki 很良心地写了两个压缩的内容，用英语能区分，但是用中文。。。
这里简单介绍下两个压缩的区别。
compaction，在 RocksDB，或者说 LSM 存储中，指的是把数据从 Ln 层，存储到 Ln+1 层这个过程，例如把重复的旧的数据删除之类的。
compression，在这里指的是数据压缩，把 1MB 的数据压缩成 500KB 这样。数据还是那些数据，只是从明文，变成了压缩之后的数据。
它们的关系大概是：
通过 Compaction 把数据压缩到不同的层，每层使用不同的 Compression 算法压缩数据，减少存储空间。

下面开始是正文。

–

压缩算法限制 LSM 树的形状。他们决定了那些排序结果可以被合并以及那些排序结果需要被一个读取操作访问。你可以参考多线程压缩了解关于 RocksDB 压缩的更多细节。

压缩算法概述

源：https://smalldatum.blogspot.com/2018/08/name-that-compaction-algorithm.html

这里我们展示一系列压缩算法：经典 Leveled，Tiered，Tiered+Leveled，Leveled-N,FIFO。除了这些，RocksDB 实现了 Tiered+Leveled 和 termed Level，Tiered termed Universal，FIFO。

经典 Leveled

经典 Leveled 压缩算法，第一次在 O’Neil et al 的 LSM-tree 论文中出现，将读操作的空间放大以及写放大最小化。

LSM 树是一系列的层。每一层都是一个排序结果，可以被按照范围切分成许多分片放到独立的文件中。每一层都比上一层大非常多倍。相邻层的大小倍数叫做扇出，当所有层之间的扇出都相同的时候，写放大会被最小化。把数据压缩进第 N 层（Ln）会把地 N-1 层（Ln-1）的数据合并到 Ln。压缩到 Ln 会把之前和并进 Ln 的数据重写。最坏情况下，每层的写放大等于扇出数，但实际操作中，通常他会比扇出数小，Hyeontaek Lim et al 的论文有相关解释。

原始 LSM 论文中的压缩算法使用 all-to-all 的 —— 所有 Ln-1 的数据会跟所有 Ln 层的数据合并。LevelDB 和 RocksDB 的则是 some-to-some 的 ——Ln-1 的部分数据和并进 Ln 层的部分数据（有覆盖的部分）

尽管 leveled 的写放大通常比 tiered 要大，但是在某些场景，leveled 是有优势的。首先是按 key 顺序插入，一个 RocksDB 的优化大大减少这种场景的写放大。另一个是有倾向性的写操作，导致只有一小块的 key 会被更新。把 RocksDB 的压缩优先级设置为正确的数值，压缩过程应该在层数最小的，拥有足够空间存储写操作的层停止 —— 他不会一致写到最大层。当 leveled 压缩是 some-to-some 模式，那么压缩只会对 LSM 树的一个写操作覆盖了的分片进行处理，这样可以让写放大比 all-to-all 模式小很多。

Leveled-N

Leveled-N 跟 Leveled 压缩算法很像，但是会有更小的写放大，更多的读放大。它允许每层拥有大于一个排序结果。压缩合并所有 Ln-1 的排序结果到 Ln 的一个排序结果中，也就是 Leveled。然后”-N“会被驾到名称中用于暗示每层可能会有 n 个排序结果。Dostoevsky 的论文定义了一个压缩算法，名称是 Fluid LSM，他最大的层有一个排序结果，但是非最大层有多于一个排序结果。leveled 压缩会在最大层完成

Tiered

Tiered 压缩通过增加读放大和空间放大，来最小化写放大。

LSM 树仍旧可以看成是 Niv Dayan 和 Stratos Idreos 论文中讲到的一系列的层。每一层有 N 个排序结果。每个 Ln 层的排序结果都比上一层的排序结果大 n 倍。压缩合并同一层的所有排序结果来构造一个下一层的新的排序结果。这里的 N 与 leveled 压缩的扇出类似。合并到下一层的时候，压缩不会读 / 重写已经排序好的 Ln 层的结果。每层的写放大是 1，远小于 Leveled 的扇出。

一个比较接近 Tiered 的实现是合并相似大小的排序结果，不必关心层的概念（这个概念会引入一个特定大小的排序结果的目标数字）。大多数（实现）包含一些主压缩的概念，也就是包含最大的排序结果，然后还有一些条件用来触发主，和非主压缩。通常的情况是会导致大量的文件以及自己。

tiered 压缩也有一些挑战：

当压缩包含一个最大层的排序结果的时候，会有一个短暂的空间放大。
对于那些比较大的排序结果，排序结果的块索引和 bloom 过滤器会比较大。把他们切小块点通常是个好主意。
大的排序结果进一步压缩会花费非常多的时间。多线程可能有帮助
压缩过程是 all-to-all 的。如果写入有倾向性，并且大多数 key 都不更新，那么大量的排序结果都可能因为 all-to-all 的压缩过程倍重写。在传统的 tiered 算法中，没办法只重写一个大排序结果的一个子集。

对于 tiered 压缩，层的概念通常是一个用于构成 LSM 树形状的概念，以及用于估算写放大。对于 RocksDB 而言，他们还是一个开发细节。L0 之上的层在 LSM 树中可以用来存储更大的排序结果。这样做的好处是可以吧排序结果切分成更小的 SST 文件。这减少了最大的 bloom 过滤器以及块索引块的大小 —— 这对于块索引更友好 —— 并且在分片索引 / 过滤倍支持之前是一个非常重要的主意。如果引入子压缩，就可以使对大块排序结果进行多线程压缩变为可能。注意 RocksDB 使用 “universal” 而不是 tiered 这个名字。

Tiered 压缩算法在 RocksDB 的代码里倍命名为 “Universal 压缩”。

Tiered+Leveled

Tiered+Leveled 会有比 leveled 更小的写放大，以及比 teired 更小的空间放大。

Tiered+Leveled 实现方式是一种混合实现，在小的层使用 tiered，在大的层使用 leveld。具体哪一层切换 tiered 和 leveled 可以非常灵活。现在我假定如果 Ln 是 leveled 那么所有之后的层（Ln+1,Ln+2）都是 leveled。

VLDB2018 的 SlimDB 是一个 tiered+leveled 的例子，机关它允许 Lk 层使用 tiered，Ln 使用 leveled，而 k>n。Fluid LSM 倍描述为 tiered+leveled 的实现，但是我认为它是 Leveled-N。

RocksDB 中的 Leveled 压缩也是 Tiered+Leveled。遵照 max_write_buffer_number 的设置，可能会有 N 个排序结果在 memtable 这一层 —— 只有一个是活跃可写的，剩下的都是只读，等待落盘的。一个 memtable 落盘过程类似于 tiered 压缩 ——memtable 的输出在 L0 构建一个新的排序结果并且不需要读 / 重写 L0 上已经存在的排序结果。根据 level0_file_num_compaction_trigger 的配置，L0 可以有多个排序结果。所以 L0 是 Teired 的。memtable 层没有压缩，所以也就没有该层是 tiered 还是 leveled 的说法。RocksDB 中 L0 的子压缩过程会更加有趣，但这是另一篇文章的内容了。

FIFO

FIFO 风格的压缩在淘汰的时候把最老的文件丢弃，可以被用于缓存数据。

选项

这里我们给出选项的概述以及他们如何影响压缩：

Options::compaction_style —— RocksDB 目前支持两种压缩算法 ——Universal 风格和 Level 风格。这个选项在这两个之间切换。可以是 kCompactionStyleUniversal 或者 kCompactionStyleLevel。如果是 kCompactionStyleUniversal，你可以用 Options::compaction_options_universal 配置 universal 风格参数。
Options::disable_auto_compactions—— 关闭自动压缩。你仍然可以选择手动压缩。
Options::compaction_filter—— 允许应用在后台压缩的时候修改 / 删除一个键值对。如果希望针对不同的压缩过程，使用不同的过滤器，客户需要提供一个 compaction_filter_factory。用户只能声明一种压缩过滤器或者工厂。
Options::compaction_filter_factory—— 一个用于提供允许应用在后台压缩的时候修改 / 删除一个键值对的过滤器的工厂。

其他会影响压缩性能以及触发条件的选项是：

Options::access_hint_on_compaction_start—— 压缩启动的时候，声明文件访问模式。对于该压缩的所有文件都会应用这个选项。默认：NORMAL
Options::level0_file_num_compaction_trigger—— 触发 level0 压缩发生的文件数量。一个负数表示 level-0 压缩不会因为文件数量而被触发。
Options::target_file_size_base 与 Options::target_file_size_multiplier—— 压缩的目标文件大小。target_file_size_base 是 level-1 的每个文件的大小。Level-L 目标文件的大小可以通过 target_file_size_base * (target_file_size_multiplier ^ (L-1)) 来计算。比如，如果 target_file_size_base 为 2MB，target_file_size_multiplier 为 10，那么 level-1 的每个文件大小就为 2MB，level2 每个文件的大小就是 20MB，level3 的文件就是 200MB。默认的 target_file_size_base 为 64MB，target_file_size_multiplier 为 1。
Options::max_compaction_bytes—— 所有压缩后的文件的最大大小。如果需要压缩的文件总大小大于这个值，我们在压缩的时候会避免展开更低级别的文件。
Options::max_background_compactions—— 后台并发执行的最大线程数，会提交给默认优先级为 LOW 的线程池。
Options::compaction_readahead_size—— 如果非零，我们在压缩的时候会做更大的读。如果你在机械硬盘上运行 RocksDB，你应该把这个值设置为至少 2MB。如果你不使用直接 IO，我们会强制设置这个为 2MB。

压缩还可以人工触发，参考人工触发压缩

参考 rocksdb/options.h 了解更多的选项信息。

Leveled 风格压缩

参考 Leveled-Compaction

Universal 风格压缩

关于 Universal 风格的压缩的描述，参考 Universal-Compaction-Style

如果你正在使用 Universal 风格的压缩，有一个 CompactionOptionsUniversal 对象，会持有该风格的所有特殊压缩配置。额外的定义在 rocksdb/universal_compaction.h，你可以在 Options::compaction_options_universal 中设置他。我们在这里简单介绍 Options::compaction_options_universal：

CompactionOptionsUniversal::size_ratio —— 比较文件大小的时候的灵活性比例。如果候选文件的大小比下一个文件小 1%，那么把下一个文件也包括进压缩候选集。默认：1
CompactionOptionsUniversal::min_merge_width —— 一次压缩中最小的文件数量。默认：2
CompactionOptionsUniversal::max_merge_width —— 一次压缩中最大的文件数量。默认：UINT_MAX
CompactionOptionsUniversal::max_size_amplification_percent —— 空间放大被定义为一个 byte 的数据存储在硬盘上需要多少额外的存储空间。例如，一个空间放大为 2% 意味着一个持有 100byte 用户数据的数据库，需要占用 102byte 的物理存储。通过这个定义，一个完全压缩的数据库的空间放大为 0%。RocksDB 用下面公式计算空间放大率：假设所有文件，除了最早的文件以外，都计算进空间放大中。默认 200，这意味着一个 100byte 的数据库可能需要占用 300byte 存储。
CompactionOptionsUniversal::compression_size_percent —— 如果这个选项被设置为 - 1（默认值），所有的输出文件都会根据指定的压缩（compress）类型进行压缩（compress）。如果这个选项不是负数，我们会尝试确保压缩（compress）大小刚好比这个值大。正常情况下，至少这个比例的数据会被压缩。当我们把压缩（compact）到一个新的文件，他是不是需要被压缩（compress）的标准是这样的：假设根据生成时间排序的文件列表如下:[A1….An B1….Bm C1….Ct]，A1 是最新的，而 Ct 时最老的，我们将把 B1…Bm 压缩 [compact]，我们计算所有的文件大小为总的大小 total_size，我们把 C1…Ct 的总大小计算为 total_C，如果 total_C /total_size < compression_size_percent，压缩（compact）输出的文件会被压缩（compress）。（这个行为看起来很诡异，但是代码确实是这么写的。。。）
CompactionOptionsUniversal::stop_style —— 停止选取下一个文件的算法条件。可以是 kCompactionStopStyleSimilarSize（选择相似大小的文件）或者 kCompactionStopStyleTotalSize（选取的文件的总大小 > 下一个文件）。默认为 kCompactionStopStyleTotalSize

FIFO 压缩风格

FIFO 压缩风格是最简单的压缩策略。很适合用于保存不是那么重要的事件日志数据（例如查询日志）。他会周期性删除旧的数据，所以基本来说，他是一种 TTL 压缩风格。

在 FIFO 压缩里，所有的文件都在 Level 0。当数据的总大小超过 CompactionOptionsFIFO::max_table_files_size 配置的大小时，我们删除最老的表文件。这意味着数据的写放大总是 1（还有 WAL 的写放大）

目前，CompactRange 函数只是强制触发压缩，然后如果有需要，删除旧的表文件。他忽略函数的参数（开始和结束 key）

由于我们不会重写键值对，我们也不会对 key 执行压缩过滤器方法。

请小心使用 FIFO 压缩风格。与其他压缩风格不同，他可能在不通知用户的情况下删除数据。

FIFO 压缩可能会导致大量 L0 文件。查询可能会变得很慢，因为最坏情况下，我们可能需要搜索所有的这些文件。即使是 bloom 过滤器也可能无法得到一个好的性能。加入有 1% 的假阳性结果，1000 个 L0 文件平均会导致 10 个假阳性结果，然后在最坏情况下，每个查询会生成 10 个 IO。用户可以选择使用更多的 bloom 位来减少假阳性结果，但是他们需要为此付出更多的内存。在某些情况下，bloom 过滤器检查的 CPU 开支可能会过高。

为了解决这个问题，用户可以选择允许一些轻量压缩发生。这可能会让写 IO 变成两倍，但是可以显著减少 L0 的文件。某些时候对于用户来说是合理的权衡。

这个功能在 5.5 版本中引入。用户可以通过 CompactionOptionsFIFO.allow_compaction = true 来打开这个功能。他会尝试选择至少 level0_file_num_compaction_trigger 个从 memtable 落盘的文件，然后合并他们。

特别的，我们总是从最新的 level0_file_num_compaction_trigger 文件开始，尝试包含尽可能多的文件进行压缩。我们使用 total_compaction_size / (number_files_in_compaction - 1) 计算已经压缩的每个文件的大小。我们总是以保证这个数字最小，并且不多于 options.write_buffer_size，这两个条件来挑选文件。在一个典型的工作场景，他总会压缩 level0_file_num_compaction_trigger 个刚落盘的文件。

例如，如果 level0_file_num_compaction_trigger = 8，每个罗盘文件为 100MB。那么只要达到了 8 个文件，他们会被压缩为一个 800MB 的文件。然后等我们有了 8 个新的 100MB 文件，他们会被压缩成第二个 800MB 的文件，以此类推。最终我们有一系列 800MB，但是不超过 8100MB 的文件。

请注意，由于最老的文件被压缩了，FIFO 删除的文件也变大了，所以可能排序好的数据会比没有压缩的数据略微少一点。

FIFO 带 TTL 压缩

一个新的，名为 FIFO 带 TTL 压缩的功能在 RocksDB5.7 被引入。

目前，FIFO 压缩目前只考虑文件总大小，比如：如果 db 的大小超过 compaction_options_fifo.max_table_files_size，丢弃最老的文件，一个个地删除知道总大小小于阈值。有时候，生产环境上打开这个，会随着有机增长把生产环境搞乱。

一个新的选项，compaction_options_fifo.ttl，被引入，用来删除超过 TTL 的 SST 文件。这个功能允许用户根据时间丢弃文件而不总是根据大小来，比如说，丢弃所有一周前或者一个月前的数据。

限制：

这个选项目前只在 max_open_files 为 - 1 时，对基于块的表格式使用。
FIFO 带 TTL 仍旧在配置的大小范围内工作，比如说，如果观察到 TTL 无法让文件总数量少于配置的大小，RocksDB 会暂时下降到基于大小的 FIFO 删除。

参考

https://wanghenshui.github.io/rocksdb-doc-cn/doc/FIFO-compaction-style.html

via：

关于压缩（Compaction）与压缩（Compression）的区别 | wanghenshui

https://wanghenshui.github.io/rocksdb-doc-cn/doc/Compaction.html

无损数据压缩算法的历史

kimy 于 2014-09-20 00:00:24 发布

引言

有两种主要的压缩算法：有损和无损。有损压缩算法通过移除在保真情形下需要大量的数据去存储的小细节，从而使文件变小。在有损压缩里，因某些必要数据的移除，恢复原文件是不可能的。有损压缩主要用来存储图像和音频文件，同时通过移除数据可以达到一个比较高的压缩率，不过本文不讨论有损压缩。无损压缩，也使文件变小，但对应的解压缩功能可以精确的恢复原文件，不丢失任何数据。无损数据压缩被广泛的应用于计算机领域，从节省你个人电脑的空间，到通过 web 发送数据。使用 Secure Shell 交流，查看 PNG 或 GIF 图片。

无损压缩算法可行的基本原理是，任意一个非随机文件都含有重复数据，这些重复数据可以通过用来确定字符或短语出现概率的统计建模技术来压缩。统计模型可以用来为特定的字符或者短语生成代码，基于它们出现的频率，配置最短的代码给最常用的数据。这些技术包括熵编码 (entropy encoding)，游程编码 (run-length encoding)，以及字典压缩。运用这些技术以及其它技术，一个 8-bit 长度的字符或者字符串可以用很少的 bit 来表示，从而大量的重复数据被移除。

历史

直到 20 世纪 70 年代，数据压缩才在计算机领域开始扮演重要角色，那时互联网变得更加流行，Lempel-Ziv 算法被发明出来，但压缩算法在计算机领域之外有着更悠久的历史。发明于 1838 年的 Morse code，是最早的数据压缩实例，为英语中最常用的字母比如 “e” 和 “t” 分配更短的 Morse code。之后，随着大型机的兴起，Claude Shannon 和 Robert Fano 发明了 Shannon-Fano 编码算法。他们的算法基于符号 (symbol) 出现的概率来给符号分配编码 (code)。一个符号出现的概率大小与对应的编码成反比，从而用更短的方式来表示符号。

两年后，David Huffman 在 MIT 学习信息理论并上了一门 Robert Fano 老师的课，Fano 给班级的同学两个选项，写一篇学期论文或者参加期末考试。Huffman 选择的是写学期论文，题目是寻找二叉编码的最优算法。经过几个月的努力后依然没有任何成果，Huffman 决定放弃所有论文相关的工作，开始学习为参加期末考试做准备。正在那时，灵感爆发，Huffman 找到一个与 Shannon-Fano 编码相类似但是更有效的编码算法。Shannon-Fano 编码和 Huffman 编码的主要区别是构建概率树的过程不同，前者是自下而上，得到一个次优结果，而后者是自上而下。

早期的 Shannon-Fano 编码和 Huffman 编码算法实现是使用硬件和硬编码完成的。直到 20 世纪 70 年代互联网以及在线存储的出现，软件压缩才被实现为 Huffman 编码依据输入数据动态产生。随后，1977 年 Abraham Lempel 和 Jacob Ziv 发表了他们独创性的 LZ77 算法，第一个使用字典来压缩数据的算法。特别的，LZ77 使用了一个叫做 slidingwindow 的动态字典。1778 年，这对搭档发表了同样使用字典的 LZ78 算法。与 LZ77 不同，LZ78 解析输入数据，生成一个静态字典，不像 LZ77 动态产生。

法律问题

LZ77 和 LZ78 都快速的流行开来，衍生出多个下图中所示的压缩算法。其中的大多数已经沉寂了，只有那么几个现在被大范围的使用，包括 DEFLATE，LZMA 以及 LZX。绝大多数常用的压缩算法都衍生于 LZ77，这不是因为 LZ77 技术更好，只是由于 Sperry 在 1984 年申请了 LZ78 衍生算法 LZW 的专利，从而发展受到了专利的阻碍，Sperry 开始因专利侵权而起诉软件提供商，服务器管理员，甚至是使用 GIF 格式但没有 License 的终端用户。

同时，UNIX 压缩工具使用了一个叫 LZC 的 LZW 算法微调整版本，之后由于专利问题而被弃用。其他的 UNIX 开发者也开始放弃使用 LZW。这导致 UNIX 社区采用基于 DEFLATE 的 gzip 和基于 Burrows-Wheeler Transform 的 bzip2 算法。长远来说，对于 UNIX 社区这是有好处的，因为 gzip 和 bzip2 格式几乎总是比 LZW 有更好的压缩比。围绕 LZW 的专利问题已经结束，因为 LZW 的专利 2003 年就到期了。尽管这样，LZW 算法已经很大程度上被替代掉了，仅仅被使用于 GIF 压缩中。自那以后，也有一些 LZW 的衍生算法，不过都没有流行开来，LZ77 算法仍然是主流。

另外一场法律官司发生于 1993，关于 LZS 算法。LZS 是由 Stac Electronics 开发的，用于硬盘压缩软件，如 Stacker。微软在开发影片压缩软件时使用了 LZS 算法，开发的软件随着 MS-DOS 6.0 一起发布，声称能够使硬盘容量翻倍。当 Stac Electronics 发现自己的知识财产被使用后，起诉了微软。微软随后被判专利侵权并赔偿 Stac Electronics1 亿 2000 万美元，后因微软上诉因非故意侵权而减少了 1360 万美元。尽管 Stac Electronics 和微软发生了一个那么大的官司，但它没有阻碍 Lempel-Ziv 算法的开发，不像 LZW 专利纠纷那样。唯一的结果就是 LZS 没有衍生出任何算法。

Deflate 的崛起

自从 Lempel-Ziv 算法被发表以来，随着对存储需求的不断增长，一些公司及其他团体开始使用数据压缩技术，这能让他们满足这些需求。然而，数据压缩并没有被大范围的使用，这一局面直到 20 世纪 80 年代末期随着互联网的腾飞才开始改变，那时数据压缩的需求出现了。带宽限额，昂贵，数据压缩能够帮助缓解这些瓶颈。当万维网发展起来之后人们开始分享更多的图片以及其它格式的数据，这些数据远比文本大得多，压缩开始变得极其重要。为了满足这些需求，几个新的文件格式被开发出来，包括 ZIP，GIF，和 PNG。

Thom Henderson 通过他的公司发布了第一个成功的商业存档格式，叫做 ARC，公司名为为 System Enhancement Associates。ARC 在 BBS 社区尤为流行，这是因为它是第一个既可以打包又可以压缩的程序，此外还开放了源代码。ARC 格式使用一个 LZW 的衍生算法来压缩数据。一个叫做 Phil Katz 的家注意到了 ARC 的流行并决定用汇编语言来重写压缩和解压缩程序，希望改进 ARC。他于 1987 发布了他的共享软件 PKARC 程序，不久被 Henderson 以侵犯版权为由起诉。Katz 被认定为有罪，并被迫支付版权费用以及其它许可协议费用。他之所以被认定侵权，是由于 PKARC 是明显抄袭 ARC，甚至于一些注释里面的错别字都相同。

Phil Katz 自 1988 年之后就因许可证问题不能继续出售 PKARC，所以 1989 年他创建了一个 PKARC 的修改版，就是现在大家熟知的 ZIP 格式。由于使用了 LZW，它被认为专利侵权的，之后 Katz 选择转而使用新的 IMPLODE 算法，这种格式于 1993 年再次被修改，那时 Kata 发布了 PKZIP 的 2.0 版本，那个版本实现了 DEFLATE 算法以及一些其它特性，如分割容量等。这个 ZIP 版本也是我们现在随处可见的格式，所有的 ZIP 文件都遵循 PKZIP 2.0 格式，尽管它年代久远。

GIF 格式，全称 Graphics Interchange Format，于 1987 年由 CompuServe 创建，允许图像无失真地被共享 (尽管这种格式被限定每一帧最多 256 种颜色)，同时减小文件的大小以允许通过数据机传输。然而，像 ZIP 格式一样，GIF 也是基于 LZW 算法。尽管专利侵权，Unisys 没有办法去阻止 GIF 的传播。即使是现在，20 年后的今天，GIF 仍然被使用着，特别是它的动画能力。

尽管 GIF 没有办法被叫停，CompuServe 需找一种不受专利束缚的格式，并于 1994 年引入了 Portable Network Graphics (PNG) 格式。像 ZIP 一样，PNG 使用 DEFLATE 算法来处理压缩。尽管 DELLATE 的专利属于 Katz，这个专利并不是强性制的，正是这样，PNG 以及其它基于 DEFLATE 的格式避免了专利侵权。尽管 LZW 在压缩历史的初期占据霸主位置，由于 Unisys 公司的好诉讼作为，LZW 慢慢的淡出主流，大家转而使用更快更高效的 DEFLATE 算法。现在 DEFLATE 是使用得最多的算法，有些压缩世界里瑞士军刀的味道。

除了用于 PNG 和 ZIP 格式之外，计算机世界里 DEFLATE 也被频繁的用在其它地方。例如 gzip (.gz) 文件格式也使用了 DEFLATE，gzip 是 ZIP 的一个开源版本。其它还包括 HTTP, SSL, 以及其它的高效压缩网络传输数据的技术。

遗憾的是，Phil Katz 英年早逝，没能看到他的 DEFLATE 算法统治计算机世界。有几年的时间他酗酒成性，生活也于 20 世纪 90 年代末期开始支离破碎，好几次因酒驾或者其它违法行为而被逮捕。Katz 于 2000 年 4 月 14 号被发现死于一个酒店的房间，终年 37 岁。死因是酒精导致的严重胰腺出血，身旁是一堆的空酒瓶。

当前的一些归档软件

ZIP 以及其它基于 DEFLATE 的格式一直占据主导地位，直到 20 世纪 90 年代中期，一些新的改进的格式开始出现。1993 年，Eugene Roshal 发布了一个叫做 WinRAR 的归档软件，该软件使用 RAR 格式。最新的 RAR 结合了 PPM 和 LZSS 算法，前面的版本就不太清楚了。RAR 开始在互联网分享文件方面成为事实标准，特别是盗版影像的传播。1996 年一个叫 bzip2d 的 Burrows-Wheeler Transform 算法开源实现发布，并很快在 UNIX 平台上面流行开来，大有对抗基于 DEFLATE 算法的 gzip 格式。1999 年另外一个开源压缩程序发布了，以 7-Zip 或.7z 的格式存在，7-Zip 应该是第一个能够挑战 ZIP 和 RAR 霸主地位的格式，这源于它的高压缩比，模块化以及开放性。这种格式并不仅限于使用一种压缩算法，而是可以在 bzip2, LZMA, LZMA2, 和 PPMd 算法之间任意选择。最后，归档软件中较新的一个格式是 PAQ * 格式。第一个 PAQ 版本于 2002 年由 Matt Mahoney 发布，叫做 PAQ1。PAQ 主要使用一种叫做 context mixing 的技术来改进 PPM 算法，context mixing 结合了两个甚至是多个统计模型来产生一个更好的符号概率预测，这要比其中的任意一个模型都要好。

压缩技术

有许多不同的技术被用来压缩数据。大多数技术都不能单独使用，需要结合起来形成一套算法。那些能够单独使用的技术比需要结合的技术通常更加有效。其中的绝大部分都归于 entropy 编码类别下面，但其它的一些技术也挺常用，如 Run-Length Encoding 和 Burrows-Wheeler Transform。

Run-Length Encoding

Run-Length Encoding 是一个非常简单的压缩技术，把重复出现的多个字符替换为重复次数外加字符。单个字符次数为 1。RLE 非常适合数据重复度比较高的数据，同一行有很多像素颜色相同的渐进图片，也可以结合 Burrows-Wheeler Transform 等其它技术一起使用。

下面是 RLE 的一个简单例子:

输入: AAABBCCCCDEEEEEEAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA

输出: 3A2B4C1D6E38A

Burrows-Wheeler Transform

Burrows-Wheeler Transform 是 1994 年发明的技术，目的是可逆的处理一段输入数据，使得相同字符连续出现的次数最大化。BWT 自身并不做任何的压缩操作，仅简单地转化数据，让 Run-Length Encoder 等压缩算法可以更有效的编码。

BWT 算法很简单:

创建一个字符串数组。
把输入字符串的所有排列组合塞入上述字符串数组。
按照字符顺序为字符串数组排序。
返回数组的最后一列。

BWT 通常处理有很多交叉重复字符的长字符串时效果很好。下面是一个有着理想输入的例子，注意 & 是文件结束符：

因为交换相同的符号到一起，输入数据在 BWT 处理之后得到优化后的结果，另外一个算法可以对该结果进行压缩，比如 RLE 会得到 “3H&3A”。尽管这个例子得到了一个较优的结果，不过现实世界中的数据它不总是这样。

Entropy Encoding

数据压缩中，平均来说为了表示一个字符或短语，Entropy 意味着所需要的最少 bit 数。一个基本的 entropy 编码器包括一个分析模型以及一套编码。输入文件被解析，并产生一个由字符出现概率组成的统计模型。然后，编码器可以利用该统计模型去决定该给每一个字符多少个 bit，从而使得最常用的字符用最短的编码，反之最不常用的字符用最长的编码。

Shannon-Fano Coding

这是最早的压缩技术，于 1949 年由 Claude Shannon 和 Robert Fano 发明。这个技术的其中一个步骤是产生一个代表字符出现概率的二叉树。字符以这样一种方式排序，出现得越频繁的字符越靠近树的顶端，越不常见的越靠近树的底部。

一个字符对应的编码通过搜索 Shannon-Fano 来获得，此外，左分支后面加 0，右分支加 1。例如，“A” 是两个左节点后接一个右节点，那么对于的编码为 “0012”。Shannon-Fano coding 不总是能够产生最优的编码，主要是由于二叉树是自下而上构建的。由于这个原因，使用的较多的还是对于任意输入都能够得到最优编码的 Huffman coding。

产生 Shannon-Fano 编码的算法很简单:

解析输入，统计每一个字符出现的频率。
根据是上述频率计算字符的概率。
依据概率对字符降序排序。
为每一个字符生成一个叶节点 (LeafNode)
把字符列表分为左右两部分，使得左边的概率与右边的概率大致相当。
左节点加编码 “0”，右节点加编码 “1”。
对两棵子树重复的步骤 5 和 6，直到所有的字符节点都成为叶子节点。

Huffman Coding

Huffman Coding 是另外一个 entropy coding 的例子，与 Shannon-Fano Coding 非常的相似，只是为了产生最优编码二叉树是自上而下构建的。

生成 Huffman 编码的算法前面的三个步骤与 Shannon-Fano 完全相同:

解析输入，统计每一个字符出现的频率。
根据是上述频率计算字符的概率。
依据概率对字符降序排序。
为每一个字符生成一个叶节点 (LeafNode)，节点包含概率信息 P，把节点存入一个队列 Queue。
While (Nodes in Queue > 1)

从队列里面取出概率最小的两个节点。
给左节点分配编码 “0”，右节点分配编码 “1”。
创建一个新的节点，其概率为上面步骤中的两个节点之和。
把两个节点中的第一个设置为新建节点的左节点，第二个节点为新建节点的右节点。
把新建节点存入队列

最后一个节点就是二叉树的根节点。

Arithmetic Coding

1979 年该算法在 IBM 被开发出来，当时 IBM 正在调研一些压缩算法，以期用于它们的大型机上。如果单论压缩比，Arithmetic coding 确实是一个最优的 entropy coding 技术，通常压缩比方面 Arithmetic Coding 要比 Huffman Coding 表现得更好。然而，它却也比其它技术复杂得多。

不像其它技术会把字符概率构建成一棵树，arithmetic coding 把输入转化为一个 0 到 1 之间的有理数，输入字符的个数记为 base，里面每一个不同的字符都分配一个 0 到 base 之间的值。然后，最后转化为二进制得到最终的结果。结果也可以通过把 base 恢复为原来的 base 值，替换为对应字符而得到原输入值。

一个基本的计算 arithmetic code 算法如下:

计算输入数据里面不同字符的个数。这个数字记为 base b (比如 base 2 代表 2 二进制)。
按字符出现的顺序分别给每一个字符分配一个 0 到 b 之间的值。
使用步骤 2 中德值，把输入中的字符替换为对应的数字 (编码)。
把步骤 3 中得到的结果从 b 进制转化为 2 进制。
如果解码需要的话，记录输入的字符总个数。

下面是一个编码操作的例子，输入为 “ABCDAABD”：

找到共有 4 个不同的字符输入，base = 4, length = 8。
按出现顺序为不同的字符赋值: A=0, B=1, C=2, D=3。
用编码替换字符，得到 “0.012300134”，注意最前面的 “0.” 是为了得到小数而加上去的。最后的 4 表示 base=4。
把 “0.012300134” 从 4 进制转化为 2 进制，得到 “0.011011000001112”。最后的 2 表示 base=2。
在结果中标识输入的总字符数为 8。

假设字符为 8 个 bit 表示，输入共需要 64 个 bit 空间，然而对应的 arithmetic coding 只有 15 个 bit，压缩比为 24%，效果显著。这个例子展示了 arithmetic coding 是如何良好的压缩固定字符串的。

压缩算法

Sliding Window Algorithms

LZ77

LZ77 发表于 1977 年，是名副其实的压缩算法开山之作。它首次引入’sliding window’ 的概念，相较几个主要的压缩算法，压缩比都有非常明显的提高。LZ77 维护了一个字典，用一个三元组来表示 offset，run length 和分割字符。offset 表示从文件起始位置到当前 Phase 的起始位置的距离，run length 记录当前 Phase 有多少个字符，分割符仅用于分割不同的 Phase。Phase 就是 offset 到 offset+length 之间的子串减掉分隔符。随着文件解析的进行，基于 sliding window 字典会动态的变化。例如，64MB 的 sliding window 意味着四点将包含 64M 的输入数据的信息。

给定一个输入为 “abbadabba”，那么输出可能像 “abb (0,1,‘d’)(0,3,‘a’)”，如下图所示:

尽管上述的替换看起来比原数据还要大，当输入数据更大一些的时候，效果会比较好。

LZR

LZR 是 LZ77 的修改版本，于 1981 年由 Michael Rodeh 发明。这个算法目标是成为 LZ77 的一个线性时间替换算法。然而，编码后 Udell 指针可能指向文件的任意 offset，意味着需要耗费可观的内存。加之压缩比表现也差强人意 (LZ77 好得多)，LZR 算是一个不成功的 LZ77 衍生算法。

DEFLATE

DEFLATE 于 1993 年由 Phil Katz 发明，是现代绝大多数压缩任务的基石。它仅仅结合了两种算法，先用 LZ77 或 LZSS 预处理，然后用 Huffman 编码，快速的得到不错的压缩结果。

DEFLATE64

DEFLATE64 是 DEFLATE 的一个有专利的扩展，把字典的大小提高到 64K (名字随之)，从而允许在 sliding window 里面有更大的距离。相比于 DEFLATE，DEFLATE64 在性能和压缩比方面都有提高。然而，由于 DEFLATE64 的专利保护以及相较 DEFLATE 并没有特别明显的提高，DEFLATE64 很少被采用。相反一些开源算法如 LZMA 被大量的使用。

LZSS

LZSS，全称 Lempel-Ziv-Storer-Szymanski，于 1982 年由 James Storer 发表。LZSS 相较 LZ77 有所提高，它能检测到一个替换是否真的减小了文件大小。如果文件大小没有减小，不再替换输入值。此外，输入段被 (offset, length) 数据对替换，其中 offset 表示离输入起始位置的 bytes 数量，length 表示从该位置读取了多少个字符。另外一个改进是去除了 “next character” 信息，仅仅使用 offset-length 数据对。

下面是一个输入为 “these theses” 简单的例子，结果为 “these (0,6) s”，仅仅节省了一个 Byte，不过输入数据大的时候效果会好得多。

LZSS 依然被用在许多使用广泛的归档格式中，其中最知名的是 RAR。LZSS 有时也被用于网络数据压缩。

LZH

LZH 发明于 1987 年，全称为 “Lempel-Ziv Huffman”。它是 LZSS 的一个衍生算法，利用 Huffman coding 压缩指针，压缩效果有微小的提高。然而使用 Huffman coding 带来的提高实在是很有限，相较于使用 Huffman coding 带来的性能损失，不足为取。

LZB

LZB 同样发明于 1987 年，同样是 LZSS 的衍生算法。如 LZH 一样，LZB 也致力于通过更加有效的编码指针以达到更好的压缩效果。它的做法是随着 sliding window 变大，逐步的增大指针的数量。它的压缩效果确实比 LZSS 和 LZH 要好，不过因为额外的编码步骤，速度上比 LZSS 慢得多。

ROLZ

ROLZ 全称 “Reduced Offset Lempel-Ziv”，它的目标是提高 LZ77 的压缩效果，通过限制 offset 的大小，从而减少为 offset-length 数据对编码的数据量。这项 LZ77 的衍生技术于 1991 年首次出现在 Ross Williams 的 LZRW4 算法里面。其它的实现包括 BALZ，QUAD，和 RZM。高度优化的 ROLZ 能够达到接近 LZMA 的压缩比，不过 ROLZ 不太流行。

LZP

LZP 全称 “Lempel-Ziv + Prediction”。它是 ROLZ 算法的一个特殊案例，offset 减小到 1。有几个衍生的算法使用不同的技术来实现或加快压缩速度，或提高压缩比的目标。LZW4 实现了一个数字编码器达到了最好的压缩比，不过牺牲了部分速度。

LZRW1

Ron Williams 于 1991 年发明了这个算法，第一次引入了 Reduced-Offset Lempel-Ziv compressiond 的概念。LZRW1 能够达到很高的压缩比，同时保持快速有效。Ron Williams 也发明另外几个基于 LZRW1 改进的衍生算法，如 LZRW1-A, 2, 3, 3-A, 和 4。

LZJB

Jeff Bonwick 于 1998 年发明了 Lempel-Ziv Jeff Bonwick 算法，用于 Solaris 操作系统的 Z 文件系统 (ZFS)。它被认为是 LZRW 算法的一个衍生算法，特别是 LZRW1，目标是改进压缩速度。既然它是被用于操作系统，速度显得尤为重要，不能因为压缩算法的原因而使得磁盘操作成为瓶颈。

LZS

Lempel-Ziv-Stac 算法于 1994 年由 Stac Electronics 发明，用于磁盘压缩软件。它是 LZ77 的一个修改版本，区分了输出的文字符号与 offset-length 数据对，此外还移除了分隔符。功能上来说，LZS 与 LZSS 算法很相似。

LZX

LZX 算法于 1995 年由 Jonathan Forbes 和 Tomi Poutanen 发明，用于 Amiga 计算机。LZX 中 X 没有什么特殊的意义。Forbes 于 1996 年把该算法出售给了微软，并且受雇于微软，那那儿该算法被继续优化并用于微软的 cabinet (.CAB) 格式。这个算法也被微软用于压缩 Compressed HTML Help (CHM) 文件，Windows Imaging Format (WIM) 文件，和 Xbox Live Avatars。

LZO

LZO 于 1996 年由 Markus 发明，该算法的目标是快速的压缩和解压缩。它允许调整压缩级别，并且在最高级别下仍仅需 64KB 额外的内存空间，同时解压缩仅需要输入和输出的空间。LZO 功能上非常类似 LZSS，不过是为了速度，而非压缩比做的优化。

LZMA

Lempel-Ziv Markov chain Algorithm 算法于 1998 年首次发表，是随着 7-Zip 归档软件一起发布的。大多数情况下它比 bzip2, DEFLATE 以及其它算法表现都要好。LZMA 使用一系列技术来完成输出。首先时一个 LZ77 的修改版本，它操作的是 bitwise 级别，而非传统上的 bytewise 级别，用于解析数据。LZ77 算法解析后的输出经过数字编码。更多的技术可被使用，这依赖于具体的 LZMA 实现。相比其它 LZ 衍生算法，LZMA 在压缩比方面提高明显，这要归功于操作 bitewise，而非 bytewise。

LZMA2

LZMA2 是 LZMA 的一个增量改进版本，于 2009 年在 7-Zip 归档软件的一个更新版本里面首次引入。LZMA2 改进了多线程处理功能，同时优化对不可压缩数据的处理，这也稍微提高了压缩效果。

Statistical Lempel-Ziv

Statistical Lempel-Ziv 是于 2001 年由 Sam Kwong 博士和 Yu Fan Ho 博士提出的一个概念。基本的原则是数据的统计分析结果可以与 LZ77 衍生算法结合起来，进一步优化什么样的编码将存储在字典中。

Dictionary Algorithms

LZ78

LZ78 于 1978 年由 Lempel 和 Ziv 发明，缩写正是来源于此。不再使用 sliding window 来生成字典，输入数据要么被预处理之后用来生成字典，或者字典在文件解析过程中逐渐形成。LZ78 采用了后者。字典的大小通常被限定为几兆的大小，或者所有编码上限为几个比特，比如 8 个。这是出于减少对内存要求的考量。算法如何处理正是 LZ78 的各个衍生算法的区别所在。

解析文件的时候，LZ78 把新碰到的字符或者字符串加到字典中。针对每一个符号，形如 (dictionary index, unknown symbol) 的字典记录会对应地生成。如果符号已经存在于字典中，那么将从字典中搜索该符号的子字符串以及其后的其它符号。最长子串的位置即为字典索引 (Index)。字典索引对应的数据被设置为最后一个未知子串。如果当前字符是未知的，那么字典索引设置为 0，表示它是单字符对。这些数据对形成一个链表数据结构。

形如 “abbadabbaabaad” 的输入，将会产生 “(0,a)(0,b)(2,a)(0,d)(1,b)(3,a)(6,d)” 这样的输出。你能从下面的例子里面看到它是如何演化的:

LZW

LZW 于 1984 年由 Terry Welch 发明，全称为 Lempel-Ziv-Welch。它是 LZ78 大家族中被用得最多的算法，尽管被专利严重的阻碍了使用。LZW 改进 LZ78 的方法与 LZSS 类似。它删除输出中冗余的数据，使得输出中不再包含指针。压缩之前它就在字典里面包含了每一个字符，也引入了一些技术改进压缩效果，比如把每一个语句的最后一个字符编码为下一个语句的第一个字符。LZW 在图像转换格式中较为常见，早期也曾用于 ZIP 格式里面，也包括一些其他的专业应用。LZW 非常的快，不过相较于一些新的算法，压缩效果就显得比较平庸。一些算法会更快，压缩效果也更好。

LZC

LZC，全称 Lempel-Ziv Compress，是 LZW 算法的一个微小修改版本，用于 UNIX 压缩工具中。LZC 与 LZW 两者的区别在于，LZC 会监控输出的压缩比。当压缩比超过某一个临界值的时候，字典被丢弃并重构。

LZT

Lempel-Ziv Tischer 是 LZC 的修改版，当字典满了，删除最不常用的的语句，用新的记录替换它。还有一些其它的小改进，不过现在 LZC 和 LZT 都不常用了。

LZMW

于 1984 年由 Victor Miller 和 Mark Wegman 发明，LZMW 算法非常类似于 LZT，它也采用了替换最不常用语句的策略。然而，不是连接字典中相似的语句，而是连接 LZMW 最后被编码的两个语句并且存储为一条记录。因此，字典的容量能够快速扩展并且 LRUs 被更频繁的丢弃掉。LZMW 压缩效果比 LZT 更好，然而它也是另外一个这个时代很难看到其应用的算法。

LZAP

LZAP 于 1988 年由 James Storer 发明，是 LZMW 算法的修改版本。AP 代表 “all prefixes”，以其遍历时在字典里面存储单个语句，字典存储了语句的所有排列组合。例如，如果最后一个语句为 “last”，当前语句是 “next”，字典将存储 “lastn”，“lastne”，“lastnex”，和 “lastnext”。

LZWL

LZWL 是 2006 年发明的一个 LZW 修改版本，处理音节而非字符。LZWL 是专为有很多常用音节的数据集而设计的，比如 XML。这种算法通常会搭配一个前置处理器，用来把输入数据分解为音节。

LZJ

Matti Jakobsson 于 1985 年发表了 LZJ 算法，它是 LZ78 大家族中唯一一位衍生于 LZW 的算法。LZJ 的工作方式是，在字典中存储每一个经过预处理输入中的不同字符串，并为它们编码。当字典满了，移除所有只出现一次的记录。

Non-dictionary Algorithms

PPM

通过抽样来预测数据是一项统计建模技术，使用输入中的一部分数据，来预测后续的符号将会是什么，通过这种算法来减少输出数据的 entropy。该算法与字典算法不一样，PPM 预测下一个符号将会是什么，而不是找出下一个符号来编码。PPM 通常结合一个编码器来一起使用，如 arithmetic 编码或者适配的 Huffman 编码。PPM 或者它的衍生算法被实现于许多归档格式中，包括 7-Zip 和 RAR。

bzip2

bzip2 是 Burrows-Wheeler Transform 算法的一个开源实现。它的操作原理很简单，不过却在压缩比和速度之间达到了一个平衡，表现良好，这让它在 UNIX 环境上很流行。首先，使用了一个 Run-Length 编码器，接下来，Burrows-Wheeler Transform 算法加入进来，然后，使用 move-to-front transform 以达到产生大量相同符号的目标，为接下来的另一个 Run-Length 编码器做准备。最后结果用 Huffman 编码，将一个消息头与其打包。

PAQ

PAQ 于 2002 年由 Matt Mahoney 发明，是老版 PPM 的一个改进版。改进的方法是使用一项叫做 context mixing 的革命性技术。Context mixing 是指智能地结合多个 (PPM 是单个模型) 统计模型，来做出对下一个符号的更好预测，比其中的任何一个模型都要好。PAQ 是最有前途的技术之一，它有很好的压缩比，开发也很活跃。自它出现后算起，有超过 20 个衍生算法被发明出来，其中一些在压缩比方面屡破记录。PAQ 的最大缺点是速度，这源于使用了多个统计模型来获得更好的压缩比。然而随着硬件速度的不断提升，它或许会是未来的标准。PAQ 在应用方面进步缓慢，一个叫 PAQ8O 的衍生算法可以在一个叫 PeaZip 的 Windows 程序里面找到，PAQ8O 支持 64-bit，速度也有较大提升。其它的 PAQ 格式仅仅用于命令行程序。