排序、DFS总结

排序

        今天上午，我们了解了冒泡排序，选择排序，插入排序，桶排序，快速排序的排序原理以及各种排序算法的复杂度和稳定性。具体原理可查阅一本通。冒泡排序，选择排序，快速排序的可视化详见这里，各种算法的复杂度和稳定性如下图所示：

1 桶(计数)排序

 桶排序的原理可详见这里，AC代码如下所示：

#include<bits/stdc++.h>
using namespace std;
int cnt[1000005];
int main()
{
	int n,x;
	cin>>n;
	while(n--)
	{
		cin>>x;
		cnt[x]++;
	}
	for(int i=0;i<=1000000;i++)
	{
		while(cnt[i]--) cout<<i<<" ";
	}
	return 0;	
}

2 排序算法 

       

 这道题是用来练习快速排序的。注意老师的这种解法和一本通上不一样，一本通上是取中间数为基准值，老师这里是用第一个元素作为基准值，这样代码会好理解一些。

核心思想:

1.在待排序的元素任取一个元素作为基准(通常选第一个元素，称为基准元素）

2.将待排序的元素进行分块，比基准元素大的元素移动到基准元素的右侧，比基准元素小的移动到作左侧，从而一趟排序过程，就可以锁定基准元素的最终位置

3.对左右两个分块重复以上步骤直到所有元素都是有序的（递归过程）

具体算法执行流程如下：

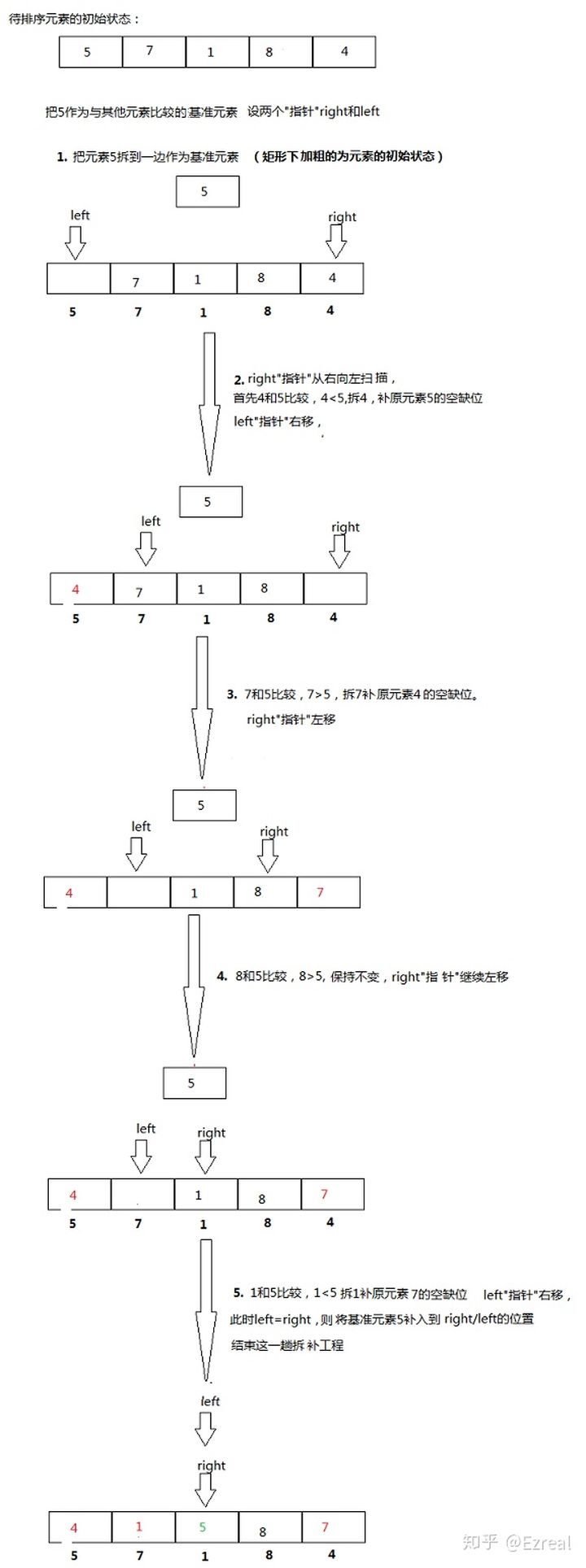
代码如下：

#include<cstdio>
int a[1005];
void quickSort(int a[],int l,int r)
{
    int i=l,j=r,temp=a[l];
    if(l<r)
    {
        while(i<j)
        {
            while(a[j]>=temp&&(i<j)) j--;
            a[i]=a[j];
            while(a[i]<=temp&&(i<j)) i++;
            a[j]=a[i];
        }
        a[i]=temp;
        quickSort(a,l,i-1);
        quickSort(a,j+1,r);
    }
}
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++) scanf("%d",&a[i]);
    quickSort(a,0,n-1);
    for(int i=n-1;i>=1;i--) printf("%d ",a[i]);printf("%d\n",a[0]);
    return 0;
}

3 结构体排序

 

这道题主要是教大家怎么用sort对结构体排序，sort的用法

1.sort函数包含在头文件为#include<algorithm>的c++标准库中，调用标准库里的排序方法可以实现对数据的排序，但是sort函数是如何实现的，我们不用考虑！

2.sort函数的模板有三个参数：

void sort (RandomAccessIterator first, RandomAccessIterator last, Compare comp);

（1）第一个参数first：是要排序的数组的起始地址。

（2）第二个参数last：是结束的地址（最后一个数据的后一个数据的地址）

（3）第三个参数comp是排序的方法：可以是从升序也可是降序。如果第三个参数不写，则默认的排序方法是从小到大排序。

 然后就是对结构体排序，自定义好相应的比较函数即可，代码如下：

#include<bits/stdc++.h>
using namespace std;
struct node
{
	string name;
	int Chinese,math,English;
}a[1005];
int cmp(node x,node y)
{
	int x_sum=x.Chinese+x.English+x.math;
	int y_sum=y.Chinese+y.English+y.math;
	if(x_sum>y_sum) return 1;
	else if(x_sum<y_sum) return 0;
	else 
	{
		if(x.Chinese>y.Chinese) return 1;
		else if(x.Chinese<y.Chinese) return 0;
		else
		{
			if(x.math>y.math) return 1;
			else if(x.math<y.math) return 0;
			else 
			{
				if(x.English>y.English) return 1;
				else if(x.English<y.English) return 0;
				else 
				{
					if(x.name>y.name) return 0;
					return 1;
				}
			}
		}
	}
}
int main()
{
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) 
	{
		cin>>a[i].name>>a[i].Chinese>>a[i].math>>a[i].English;
	}
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++)
	{
		cout<<a[i].name<<" "<<a[i].Chinese<<" "<<a[i].math<<" "<<a[i].English<<endl;
	}
	return 0;
}

4 稳定排序

 

题目先给出一个未排好序的数组，然后给出一个降序排序后的数组，问给出的排序后的数据是否是稳定的排序。由于sort是根据数据特性结合插入，快速，堆排序三种排序算法实现，不能保证稳定性，但是我们可以在结构体里多定义一个序号，利用序号来达到稳定排序的目的，排好序后再和题目给定的数据比对即可。代码如下：

#include<bits/stdc++.h>
using namespace std;
struct node
{
	char c;
	int s;
	int id;
}a[1005],b[1005];
int n;
int cmp(node x,node y)
{
	if(x.s==y.s)
	{
		if(x.id<y.id) return 1;
		return 0;
	}
	if(x.s>y.s) return 1;
	return 0;
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i].c>>a[i].s;
		a[i].id=i;
	}
	for(int i=1;i<=n;i++)
	{
		cin>>b[i].c>>b[i].s;
	}
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++)
	{
		if(a[i].c!=b[i].c||a[i].s!=b[i].s)
		{
			cout<<"NO"<<endl;
			return 0;
		}
	}
	cout<<"YES"<<endl;
	return 0;
}

DFS(深度优先搜索)

今天下午，我们初步学习了DFS，先是解决了联通块问题，然后解决了全排列问题。初步体验了DFS的用法。

1 连通块问题

 本题处理好自身之后，继续处理相邻的8个方向即可，刚好可以用两重循环来表示。这种类型的题目千万要注意处理好边界。AC代码如下：

#include<bits/stdc++.h>
using namespace std;
char a[1005][1005];
int n,m;
void dfs(int x,int y)
{
	a[x][y]='.';
	for(int i=-1;i<=1;i++)
	{
		for(int j=-1;j<=1;j++)
		{
			int nx=x+i,ny=y+j;
			if(1<=nx&&nx<=n&&1<=ny&&ny<=m)
			{
				if(a[nx][ny]=='W') dfs(nx,ny);
			}
		}
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		scanf("%s",a[i]+1);
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(a[i][j]=='W')
			{
				dfs(i,j);
				ans++;
			}
		}
	}
	cout<<ans<<endl;
	return 0;
}

2 DFS(n!全排列)

 

 解题思路：如果是求两个数的全排列，我们很容易想到解法，就是两重循环，然后判断值不相等即可，代码如下：

#include<bits/stdc++.h>
using namespace std;
int main()
{
	for(int i=1;i<=2;i++)
	{
		for(int j=1;j<=2;j++)
		{
			if(j!=i) 
			{
				cout<<i<<" "<<j<<endl;
			}
		}
	}
	return 0;
} 

同理，3个数的全排列，代码可以这样写：

#include<bits/stdc++.h>
using namespace std;
int main()
{
	for(int i=1;i<=3;i++)
	{
		for(int j=1;j<=3;j++)
		{
			for(int k=1;k<=3;k++)
			{
				if(i!=j&&i!=k&&j!=k)
				{
					cout<<i<<" "<<j<<" "<<k<<endl;
				}
			}
		}
	}
	return 0;
} 

但是我们这样写有个不好的地方就是当n越来越大是，判断不相等的条件越来越不好写，我们可以换一种策略，就是标记变量，用过的标记一下，下一层循环不再使用，然后循环完再还原。代码如下：

#include<bits/stdc++.h>
using namespace std;
int vis[11];
int main()
{
	for(int i=1;i<=3;i++)
	{
		vis[i]=1;
		for(int j=1;j<=3;j++)
		{
			if(vis[j]==1) continue;
			vis[j]=1;
			for(int k=1;k<=3;k++)
			{
				if(vis[k]==0)
				{
					cout<<i<<" "<<j<<" "<<k<<endl;
				}
			}
			vis[j]=0;
		}
		vis[i]=0;
	}
	return 0;
} 

同理n=4的时候全排列可以写成：

#include<bits/stdc++.h>
using namespace std;
int vis[11];
int main()
{
	for(int i=1;i<=4;i++)
	{
		vis[i]=1;
		for(int j=1;j<=4;j++)
		{
			if(vis[j]==1) continue;
			vis[j]=1;
			for(int k=1;k<=4;k++)
			{
				if(vis[k]==1) continue;
				vis[k]=1;
				for(int p=1;p<=4;p++)
				{
					if(vis[p]==0)
					{
						cout<<i<<" "<<j<<" "<<k<<" "<<p<<endl;
					}
				}
				vis[k]=0;
			}
			vis[j]=0;
		}
		vis[i]=0;
	}
	return 0;
} 

那n更大的时候呢？这样写代码也效率低下了(这里不是指运行效率低，而是指代码太长了)，有没有办法对于动态的n，我生成动态的n重循环呢？答案显然是可以的，那就是利用递归，它可以对于动态的n实现动态的n重循环。代码如下：

#include<bits/stdc++.h>
using namespace std;
int ans[11],vis[11],n;
void dfs(int d)
{
	if(d==n+1)
	{
		for(int i=1;i<n;i++) cout<<ans[i]<<" ";
		cout<<ans[n]<<endl;
		return ;
	}
	for(int i=1;i<=n;i++)
	{
		if(vis[i]==0)
		{
			ans[d]=i;
			vis[i]=1;
			dfs(d+1);
			vis[i]=0;	
		} 
	}
}
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) vis[i]=0;
	dfs(1);
	return 0;
}

完结！撒花！