梯度攻击实现降低手写识别率

1 简介

本文主要实现在手写模型识别率为0.98左右的情况下，通过FGSM和PGD方式梯度攻击模型后，识别率降到0.1以下，也简单对比了两种方式的攻击效果。

2 实验过程

源代码见本人上传资源。
首先生成识别模型，识别率在98%左右，手写识别数据已经下载到文件夹内，手写识别模型代码：

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.autograd import Variable
import numpy as np
import matplotlib.pyplot as plt

#训练分类模型：
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return x


device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')  # 启用GPU
train_loader = torch.utils.data.DataLoader(  # 加载训练数据
    datasets.MNIST('datasets', train=True, download=True,
                   transform=transforms.Compose([
                       transforms.ToTensor(),
                       transforms.Normalize((0.1307,), (0.3081,))
                   ])),
    batch_size=64, shuffle=True)

model = Net()
model = model.to(device)
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)  # 初始化优化器

for epoch in range(1, 10 + 1):  # 共迭代10次
    for batch_idx, (data, target) in enumerate(train_loader):
        data = data.to(device)
        target = target.to(device)
        data, target = Variable(data), Variable(target)
        optimizer.zero_grad()
        output = model(data)  # 代入模型
        loss = F.cross_entropy(output, target)
        loss.backward()
        optimizer.step()
        if batch_idx % 100 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                       100. * batch_idx / len(train_loader), loss.item()))

torch.save(model, 'datasets/model.pth')  # 保存模型

生成的模型准确率在98%左右，然后下一步进行攻击：当USE_PGD = True 时为使用PGD方式攻击，为False时为使用FGSM方式攻击；

#攻击
USE_PGD = True
##USE_PGD = False
def draw(data):
    ex = data.squeeze().detach().cpu().numpy()
    plt.imshow(ex, cmap="gray")
    plt.show()


def test(model, device, test_loader, epsilon, t=5, debug=False):
    correct = 0
    adv_examples = []

    for data, target in test_loader:
        data, target = data.to(device), target.to(device)
        data.requires_grad = True  # 以便对输入求导 ** 重要 **
        output = model(data)
        init_pred = output.max(1, keepdim=True)[1]
        if init_pred.item() != target.item():  # 如果不扰动也预测不对，则跳过
            continue
        if debug:
            draw(data)

        if USE_PGD:
            alpha = epsilon / t  # 每次只改变一小步
            perturbed_data = data
            final_pred = init_pred
            # while target.item() == final_pred.item(): # 只要修改成功就退出
            for i in range(t):  # 共迭代 t 次
                if debug:
                    print("target", target.item(), "pred", final_pred.item())
                loss = F.cross_entropy(output, target)
                model.zero_grad()
                loss.backward(retain_graph=True)
                data_grad = data.grad.data  # 输入数据的梯度 ** 重要 **

                sign_data_grad = data_grad.sign()  # 取符号（正负）
                perturbed_image = perturbed_data + alpha * sign_data_grad  # 添加扰动
                perturbed_data = torch.clamp(perturbed_image, 0, 1)  # 把各元素压缩到[0,1]之间

                output = model(perturbed_data)  # 代入扰动后的数据
                final_pred = output.max(1, keepdim=True)[1]  # 预测选项
                if debug:
                    draw(perturbed_data)
        else:
            loss = F.cross_entropy(output, target)
            model.zero_grad()
            loss.backward()

            data_grad = data.grad.data  # 输入数据的梯度 ** 重要 **
            sign_data_grad = data_grad.sign()  # 取符号（正负）
            perturbed_image = data + epsilon * sign_data_grad  # 添加扰动
            perturbed_data = torch.clamp(perturbed_image, 0, 1)  # 把各元素压缩到[0,1]之间

            output = model(perturbed_data)  # 代入扰动后的数据
            final_pred = output.max(1, keepdim=True)[1]

        # 统计准确率并记录，以便后面做图
        if final_pred.item() == target.item():
            correct += 1
            if (epsilon == 0) and (len(adv_examples) < 5):
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(), final_pred.item(), adv_ex))
        else:  # 保存扰动后错误分类的图片
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append((init_pred.item(), final_pred.item(), adv_ex))

    final_acc = correct / float(len(test_loader))  # 计算整体准确率
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))
    return final_acc, adv_examples


epsilons = [0, .05, .1, .15, .2, .25, .3]  # 使用不同的调整力度
pretrained_model = "datasets/model.pth"  # 使用的预训练模型路径

test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('datasets', train=False, download=True, transform=transforms.Compose([
        transforms.ToTensor(),
    ])),
    batch_size=1, shuffle=True
)
model = torch.load(pretrained_model, map_location='cpu').to(device)
model.eval()

accuracies = []
examples = []
for eps in epsilons:  # 每次测一种超参数
    acc, ex = test(model, device, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)

最后绘制图，显示攻击效果：

# 做图
plt.figure(figsize=(8, 5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()

cnt = 0
plt.figure(figsize=(8, 10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons), len(examples[0]), cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
        orig, adv, ex = examples[i][j]
        plt.title("{} -> {}".format(orig, adv))
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()

注意这三部分是放到一个Python文件中运行的，运行完毕后结果图：

在FGSM攻击下：

准确率从0.98 降低到最后的0.09。

在PGD攻击下：

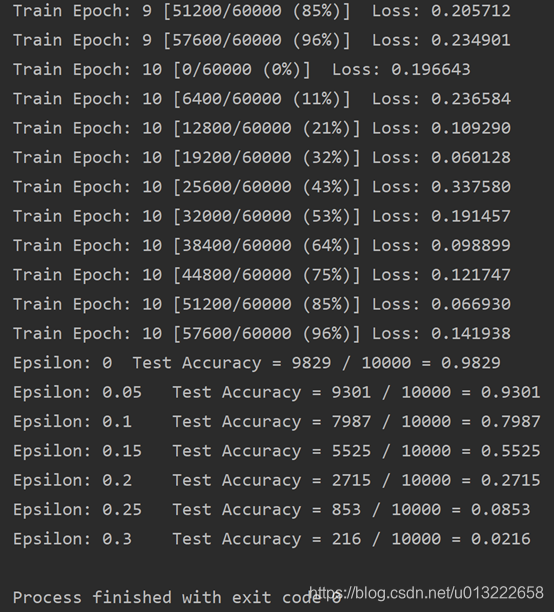
准确率从0.98降到0.02.可以看出PGD效果比FGSM要好，但是使用的训练时间也长。

3 参考博文

参考博文链接：https://blog.youkuaiyun.com/xieyan0811/article/details/104790915

4 代码下载链接

https://download.youkuaiyun.com/download/u013222658/12350519