本文深入解析Logistic回归，探讨其作为分类算法而非回归的原因，介绍了Sigmoid函数及其在概率估计中的作用。通过示例展示了代价函数的形式，并分析了为何采用梯度下降法求解参数。此外，还提及了随机梯度下降法在大量样本时的效率优势。
概述：
在网络上搜索了很多文章，此篇文章结合了多个文章的资料与图片。
什么是逻辑回归
逻辑回归在某些书中也被称为对数几率回归，明明被叫做回归，却用在了分类问题上，我个人认为这是因为逻辑回归用了和回归类似的方法来解决了分类问题。
假设有一个二分类问题，输出为y∈{0,1}，而线性回归模型产生的预测值为z=wTx+b是实数值，我们希望有一个理想的阶跃函数来帮我们实现z值到0/1的转化。
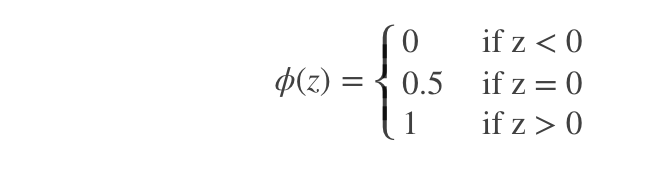
然而该函数不连续，我们希望有一个单调可微的函数来供我们使用，于是便找到了Sigmoid functionSigmoid function来替代。
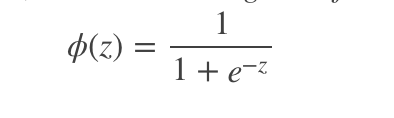
两者的图像如下图所示
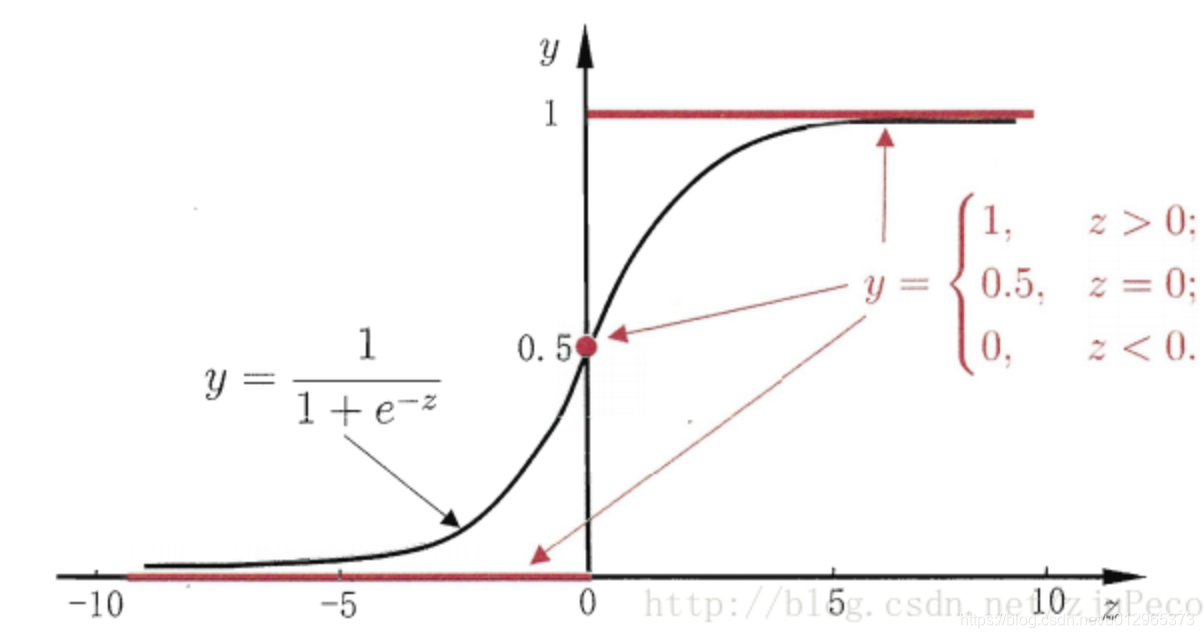
有了Sigmoid fuction之
订阅专栏 解锁全文
扫一扫
1513
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
