机器学习实战解读-K近邻算法
K-近邻算法是属于监督学习,对类别分类样本数据比较苛刻,需要比较准确且有一定量的样本数据作为分类的基础。具体主要包括以下内容:
- K-近邻算法介绍
- 数据选择及处理
- 算法知识点
- 源码编写与测试
- 应用环境介绍
- 优缺点总结
K-近邻算法介绍
k-近邻算法是采用测量不同特征值之间的距离来进行分类的算法
K-近邻算法是属于监督分类,需要精确的样本数据进行支撑,其基本原理是基础的样本数据是算法的训练样本集,样本的每一个数据都有对应的标签值,即每一个数据组对应的不同特征值所属的类别是固定的,如[1.0,1,0]是属于类别A,或者用一个现实的例子,[哺乳动物,直立行走,群落生活],可能细分的是猿类,如果再细分为有独立思考能力,那可能就是人类。所以样本数据的分类一定要是比较准确的,而选择特征值则是要根据样本数据实际情况进行选择。
样本数据对应标签集是分类的基础,通过计算输入的新数据特征值与样本集数据的特征值之间的距离来进行比较,距离越小,说明相似度越高,通过对距离值递增排序,选取前k个值,统计对应的样本属于类别,按照类别占比,比例最高的即是输入数据所属的类别。
距离是计算类别之间相似度的一种表达方式,常见的距离有欧氏距离、拉格朗日距离等,这里采用欧氏距离。
欧氏距离公式:
数据选择与处理
k-近邻算法的源样本数据包括两个部分,一是样本标签数据;二是样本数据。
样本数据与样本标签数据是一一对应的。由于k-近邻算法主要针对结构化的数据,所以特征数据的选择尽可能的转化为数值型,而且特征值有比较明显的区分做哟个,如电影的分类,爱情片和动作片,最主要的区分点是亲吻镜头和打斗镜头,对每部电影的这两个镜头数进行统计,可以很好的区分爱情片和动作片。
算法知识点
在进行数据预处理和算法设计过程中,会使用到python的一个比较重要的包:
numpy。numpy主要用来进行科学计算和矩阵数据处理,包含的许多函数可以很方便进行数据的处理。在这里主要用的函数如下:
1、dataSet.shape[0]:shape用来计算矩阵数组的行数和列数,shape[0]是行数,shape[1]是列数。
2、tile():该函数功能是复制,由于样本集是一个矩阵数组,所以输入的向量的列,也就是特征值是和样本矩阵的列是一致的,但是要保证向量和所有的样本数据计算距离值,就要将向量扩充为同一样行数的矩阵数组,tile(inX,(dataSet.shape[0],1))表示的意思就是行复制dataSet.shape[0]次,列复制一次。
3、sum():在numpy中计算矩阵的和,其参数为axis,有三个值,0表示所有的行列数计算求和;1表示计算矩阵每一行的和;2表示计算矩阵每一列的和。
源码编写和测试
from numpy import *
import operator
from os import listdir
def classify0(inX, dataSet, labels, k):
dataSetSize = dataSet.shape[0]
diffMat = tile(inX, (dataSetSize,1)) - dataSet
sqDiffMat = diffMat**2
sqDistances = sqDiffMat.sum(axis=1)
distances = sqDistances**0.5
sortedDistIndicies = distances.argsort()
classCount={}
for i in range(k):
voteIlabel = labels[sortedDistIndicies[i]]
classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
def createDataSet():
group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
labels = ['A','A','B','B']
return group, labels
def file2matrix(filename):
fr = open(filename)
numberOfLines = len(fr.readlines()) #get the number of lines in the file
returnMat = zeros((numberOfLines,3)) #prepare matrix to return
classLabelVector = [] #prepare labels return
fr = open(filename)
index = 0
for line in fr.readlines():
line = line.strip()
listFromLine = line.split('\t')
returnMat[index,:] = listFromLine[0:3]
classLabelVector.append(int(listFromLine[-1]))
index += 1
return returnMat,classLabelVector
def autoNorm(dataSet):
minVals = dataSet.min(0)
maxVals = dataSet.max(0)
ranges = maxVals - minVals
normDataSet = zeros(shape(dataSet))
m = dataSet.shape[0]
normDataSet = dataSet - tile(minVals, (m,1))
normDataSet = normDataSet/tile(ranges, (m,1)) #element wise divide
return normDataSet, ranges, minVals
def datingClassTest():
hoRatio = 0.50 #hold out 10%
datingDataMat,datingLabels = file2matrix('datingTestSet2.txt') #load data setfrom file
normMat, ranges, minVals = autoNorm(datingDataMat)
m = normMat.shape[0]
numTestVecs = int(m*hoRatio)
errorCount = 0.0
for i in range(numTestVecs):
classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
if (classifierResult != datingLabels[i]): errorCount += 1.0
print "the total error rate is: %f" % (errorCount/float(numTestVecs))
print errorCount
def img2vector(filename):
returnVect = zeros((1,1024))
fr = open(filename)
for i in range(32):
lineStr = fr.readline()
for j in range(32):
returnVect[0,32*i+j] = int(lineStr[j])
return returnVect
def handwritingClassTest():
hwLabels = []
trainingFileList = listdir('trainingDigits') #load the training set
m = len(trainingFileList)
trainingMat = zeros((m,1024))
for i in range(m):
fileNameStr = trainingFileList[i]
fileStr = fileNameStr.split('.')[0] #take off .txt
classNumStr = int(fileStr.split('_')[0])
hwLabels.append(classNumStr)
trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
testFileList = listdir('testDigits') #iterate through the test set
errorCount = 0.0
mTest = len(testFileList)
for i in range(mTest):
fileNameStr = testFileList[i]
fileStr = fileNameStr.split('.')[0] #take off .txt
classNumStr = int(fileStr.split('_')[0])
vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)
if (classifierResult != classNumStr): errorCount += 1.0
print "\nthe total number of errors is: %d" % errorCount
print "\nthe total error rate is: %f" % (errorCount/float(mTest))应用环境介绍
k-近邻算法的原理比较简单,分类的效果也取决与样本数据的精确度和k值的选择。应用场景如带有个性标签的求职推荐和招聘人员的针对性推荐,要求职业标签详细且有代表性,如python开发、JavaWeb开发等计算机行业的人员标签;销售、推销、推广等销售行业的标签等。
优缺点总结
k-近邻算法的优点是样本数据比较全的情况下,分类的效果会比较好。缺点是算法分类的局限性比较多,如应用场景要求分类特点比较明确,k值的选择以及样本数据的量。同时该算法由于计算复杂度和空间复杂度比较高,所以在处理样本数据较大及待分类数据较多的情况下,分类的时间会比较长,性能相对要低。
注:算法的代码是引用了书本机器学习实践,自己写的代码在别的电脑里,希望大家多多提提意见,谈谈自己对该算法或者其他算法的理解和建议。
 K近邻算法详解与实战
K近邻算法详解与实战





 本文介绍了K-近邻算法,属于监督学习,依赖准确的样本数据。算法基于样本间距离计算相似度,常用距离度量为欧氏距离。讨论了数据选择与处理、算法实现、应用环境及优缺点。适合结构化数据的分类,但计算复杂度高,对样本量和k值敏感。
本文介绍了K-近邻算法,属于监督学习,依赖准确的样本数据。算法基于样本间距离计算相似度,常用距离度量为欧氏距离。讨论了数据选择与处理、算法实现、应用环境及优缺点。适合结构化数据的分类,但计算复杂度高,对样本量和k值敏感。
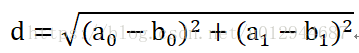
















 1115
1115

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








