模型评估与优化：留出法、交叉验证与自助法-优快云博客

本文链接：https://blog.youkuaiyun.com/u012867518/article/details/115306905

1. 分类模型的评估

1.1 评估方法

1.1.1 留出法

“留出法” ( hold-out）直接将数据集 $D$ 划分为两个互斥的集合，其中一个集合作为训练集 $S$ ，另一个作为测试集 $T$ ，即 $\cup T , S\cap T ＝\varnothing$ 。在 $S$ 上训练出模型后，用 $T$ 来评估其测试误差，作为对泛化误差的估计．以二分类任务为例，假定包含 1000 个样本，将其划分为 $S$ 包含 700 个样本， $T$ 包含 300 个样本，用 $S$ 进行训练后，如果模型在 $T$ 上有 90个样本分类错误，那么其错误率为（ 90 / 300 ) x 100 % = 30 % ，相应的，精度为 1 -30％= 70 % 。

训练／测试集的划分要尽可能保持数据分布的一致性，避免因数据划分过程引入额外的偏差而对最终结果产生影响，例如在分类任务中至少要保持样本的类别比例相似。如果从采样的角度来看待数据集的划分过程，则保留类别比例的采样方式通常称为“分层采样”。例如通过对 $D$ 进行分层采样而获得含 70 ％样本的训练集 $S $和含 30 ％样本的侧试集 $T$ ，若 $D$ 包含 500个正例、 500个反例，则分层采样得到的 $S$ 应包含 350 个正例、 350 个反例，而 $T$ 则包含 150 个正例和 150 个反例；若$ S 、T $中样本类别比例差别很大，则误差估计将由于训练／侧试数据分布的差异而产生偏差．

单次使用留出法得到的估计结果往往不够稳定可靠，在使用留出法时，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果．例如进行 100 次随机划分，每次产生一个训练／测试集用于实验评估， 100 次后就得到 100 个结果，而留出法返回的则是这 100 个结果的平均。

另外，一般将总样本的 $\sim 4/5$ 用作训练，剩余样本用于测试。

1.1.2 K折交叉验证

“交叉验证法” ( cross vahdation ）先将数据集 $D$ 划分为 $k$ 个大小相似的互斥子集，即 $D=D_1 \cup D_2 \cup \cdots \cup D_k\cup,D_i \cap D_j =\varnothing(i \neq j)$ .每个子集 $D_i$ 都尽可能保持数据分布的一致性，即从 $D$ 中通过分层采样得到．然后，每次用 $k - 1$ 个子集的并集作为训练集，余卜的那个子集作为测试集；这样就可获得 $k$ 组训练／测试集，从而可进行 $k$ 次训练和测试，最终返回的是这 $k$ 个测试结果的均值．显然，交叉验证法评估结果的稳定性和保真性在很大程度上取决于 $k$ 的取值，为强调这一点，通常把交叉验证法称为“ $k$ 折交叉验证” ( $k-fold\;\; cross validation$ ) . $k$ 最常用的取值是 10 ，此时称为 10 折交叉验证；其他常用的 $k$ 值有 5 、 20 等。

与留出法相似，将数据集 $D$ 划分为 $k$ 个子集同样存在多种划分方式．为减小因样本划分不同而引入的差别， $k$ 折交叉验证通常要随机使用不同的划分重复 $p$ 次，最终的评估结果是这 $p$ 次 $k$ 折交叉验证结果的均值，例如常见的有 " 10 次 10 折交叉验证” 。

假定数据集 $D$ 中包含 $m$ 个样本，若令 $k = m$ ，则得到了交叉验证法的一个特例：留一法（ Leave- One - Out ，简称 LOO ) ．显然，留一法不受随机样木划分方式的影响，因为 $m$ 个样本只有唯一的方式划分为 $m$ 个子集——每个子集包含一个样本；留一法使用的训练集与初始数据集相比只少了一个样本，这就使得在绝大多数情况下，留一法中被实际评估的模型与期望评估的用 $D$ 训练出的模型很相似，因此，留一法的评估结果往往被认为比较准确．

然而，留一法也有其缺陷：在数据集比较大时，训练 $m$ 个模型的计算开销可能是难以忍受的（例如数据集包含 1百万个样本，则需训练1百万个模型），而这还是在未考虑算法调参的情况下。另外，留一法的估计结果也未必永远比其他评估方法准确；“没有免费的午餐”定理对实验评估方法同样适用。

1.1.3 自助法

“自助法”(bootstrapping)是一个比较好的解决方案，它直接以自助采样法(bootstrap sampling)为基础，给定包含 $m$ 个样本的数据集 $D,$ 我们对它进行采样产生数据集 $D^{\prime}:$ 每次随机从 $D$ 中挑选一个样本, 将其考贝放入 $D^{\prime},$ 然后再将该样本放回初始数据集 $D$ 中, 使得该样本在下次采样时仍有可能被采到; 这个过程重复执行 $m$ 次后, 我们就得到了包含 $m$ 个样本的数据集 $D^{\prime},$ 这就是自助采样的结果. 显然, $D$ 中有一部分样本会在 $D^{\prime}$ 中多次出现，而另一部分样本不出现. 可以做一个简单的估计, 样本在 $m$ 次采样中始终不被采到的概率是 $\left(1-\frac{1}{m}\right)^{m},$ 取极限得到
$\lim _{m \mapsto \infty}\left(1-\frac{1}{m}\right)^{m} \mapsto \frac{1}{e} \approx 0.368$
即通过自助采样, 初始数据集 $D$ 中约有 $\%$ 的样本未出现在采样数据集 $D^{\prime}$ 中. 于是我们可将 $D^{\prime}$ 用作训练集, $\ D ′ D \backslash D^{\prime}$ 用作测试集; 这样, 实际评估的模型与期望评估的模型都使用 $m$ 个训练样本, 而我们仍有数据总量约 $1 / 3$ 的、没在训练集中出现的样本用于测试. 这样的测试结果, 亦称“包外估计” (out-of-bagestimate).
自助法在数据集较小、难以有效划分训练/测试集时很有用; 此外，自助法能从初始数据集中产生多个不同的训练集, 这对集成学习等方法有很大的好处.然而，自助法产生的数据集改变了初始数据集的分布, 这会引入估计偏差。因此，在初始数据量足够时，留出法和交叉验证法更常用一些。

1.2 学习曲线与验证曲线

1.2.1 学习曲线

学习曲线就是通过画出不同训练集大小时训练集和交叉验证的准确率，可以看到模型在新数据上的表现，进而来判断模型是否方差偏高或偏差过高，以及增大训练集是否可以减小过拟合。函数如下：

sklearn.learning_curve.``learning_curve(estimator, X, y, train_sizes=array([ 0.1, 0.33, 0.55, 0.78, 1. ]), cv=None, scoring=None, exploit_incremental_learning=False, n_jobs=1, pre_dispatch=‘all’, verbose=0)

参数解析：

estimator：所使用的分类器

X: array-like, shape (n_samples, n_features)

训练向量，n_samples是样本的数量，n_features是特征的数量

y: array-like, shape (n_samples) or (n_samples, n_features), 可选。

相对于X的目标以进行分类或回归；对于无监督学习，无此限制。

train_sizes: array-like of shape (n_ticks,), default=np.linspace(0.1, 1.0, 5)

用于生成学习曲线的相对或绝对数量的训练样本。如果dtype为float，则视为训练集最大规模的一部分（由所选验证方法确定），即它必须在（0，1]之内，否则将被解释为训练集的绝对大小。请注意，为进行分类，样本数量通常必须足够大，每个类至少包含一个样本。（默认值：np.linspace(0.1, 1.0, 5))

cv: int, cross-validation generator or an iterable, optional

确定交叉验证切分策略。cv值可以输入：

None，默认使用5折交叉验证
int，用于指定(Stratified)KFold的折数
CV splitter
可迭代输出训练集和测试集的切分作为索引数组

对于int或 None输入，如果估计器是分类器，并且y是二分类或多分类，则使用StratifiedKFold。在所有其他情况下，均使用KFold。

n_jobs : 整数，可选并行运行的作业数（默认值为1）。windows开多线程需要在"name"==__main__中运行。

verbose : integer, optional

控制冗余：越高，有越多的信息

返回值：

train_sizes_abs：array, shape = (n_unique_ticks,), dtype int

用于生成learning curve的训练集的样本数。由于重复的输入将会被删除，所以ticks可能会少于n_ticks.

train_scores : array, shape (n_ticks, n_cv_folds)

在训练集上的分数

test_scores : array, shape (n_ticks, n_cv_folds)

在测试集上的分数

【例子】

pipe_lr3 = make_pipeline(StandardScaler(), LogisticRegression(random_state=1,penalty='l2'))
train_sizes,train_scores,test_scores = learning_curve(estimator=pipe_lr3,X=X_train,y=y_train,train_sizes=np.linspace(0.1, 1, 10), cv=10, n_jobs=1)
# np.linspace(0.1, 1, 10)  表示0.1到1划分10个数据点
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(train_sizes, train_mean, color='blue', marker='o', markersize=5, label='training accuracy')
plt.fill_between(train_sizes, train_mean + train_std, train_mean - train_std, alpha=0.15, color='blue')
plt.plot(train_sizes, test_mean, color='red', marker='s', markersize=5, label='validation accuracy')
plt.fill_between(train_sizes, test_mean + test_std, test_mean - test_std, alpha=0.15, color='red')
plt.xlabel("Number of training samples")
plt.ylabel("Accuracy")
plt.legend(loc='lower right')
plt.ylim([0.8, 1.02])
plt.savefig('picture/learning_curve.png')
plt.show()

1.2.2 验证曲线

验证曲线是一种通过定位过拟合、欠拟合等诸多问题的方法，帮助提高模型性能的有效工具。验证曲线绘制的是准确率与模型参数之间的关系。函数如下：

sklearn.model_selection.``validation_curve(estimator, X, y, ***, param_name, param_range, groups=None, cv=None, scoring=None, n_jobs=None, pre_dispatch=‘all’, verbose=0, error_score=nan, fit_params=None)

参数解析：

param_name: str ，将要改变的参数名称,比如SVM的gamma参数

param_range :array-like of shape (n_values,) 将要评估的参数值。

【例子】

pipe_lr3 = make_pipeline(StandardScaler(),LogisticRegression(random_state=1,penalty='l2'))
param_range = [0.001,0.01,0.1,1.0,10.0,100.0]
train_scores,test_scores = validation_curve(estimator=pipe_lr3,X=X_train,y=y_train,param_name='logisticregression__C',param_range=param_range,cv=10,n_jobs=1)
train_mean = np.mean(train_scores,axis=1)
train_std = np.std(train_scores,axis=1)
test_mean = np.mean(test_scores,axis=1)
test_std = np.std(test_scores,axis=1)
plt.plot(param_range,train_mean,color='blue',marker='o',markersize=5,label='training accuracy')
plt.fill_between(param_range,train_mean+train_std,train_mean-train_std,alpha=0.15,color='blue')
plt.plot(param_range,test_mean,color='red',marker='s',markersize=5,label='validation accuracy')
plt.fill_between(param_range,test_mean+test_std,test_mean-test_std,alpha=0.15,color='red')
plt.xscale('log')
plt.xlabel("Parameter C")
plt.ylabel("Accuracy")
plt.legend(loc='lower right')
plt.ylim([0.8,1.02])
plt.show()

验证曲线和学习曲线的区别是，横轴为某个超参数的一系列值，由此来看不同参数设置下模型的准确率，而不是不同训练集大小下的准确率。

从验证曲线上可以看到随着超参数设置的改变，模型可能从欠拟合到合适再到过拟合的过程，进而选择一个合适的设置，来提高模型的性能。

2. 分类模型评估指标

2.1 指标

True Positive：若一个实例是正类，并且被预测为正类，即为真正类TP（真阳性）
False Negative：若一个实例是正类，但是被预测为负类，即为假负类FN（假阴性）
False Positive：若一个实例是负类，但是被预测为正类，即为假正类FP（假阳性）
True Negative：若一个实例是负类，并且被预测为负类，即为真负类TN（真阴性）

误差率

$ERR==\frac{F P+F N}{F P+F N+T P+T N}$

准确率（Accuracy）
$ACC=\frac{T P+T N}{F P+F N+T P+T N}$
假阳率（False Positive Rate, FPR）
$FPR=\frac{F P}{N}=\frac{F P}{F P+T N}$
在所有实际为阴性的样本中，被错误地判定为阳性之比率
真阳率（True Positive Rate，TPR）
$TPR=\frac{T P}{P}=\frac{T P}{F N+T P}$
在所有实际为阳性的样本中，被正确地判断为阳性之比率
精准度（Precision）

$PRE=\frac{T P}{T P+F P}$

召回率（Recall）
$R=\frac{T P}{P}=\frac{T P}{F N+T P}$
F1-score
$\frac{PRE \times REC}{PRE+REC}$

2.2 混淆矩阵

混淆矩阵（Confusion Matrix）是机器学习中用来总结分类模型预测结果的一个分析表，是模式识别领域中的一种常用的表达形式。它以矩阵的形式描绘样本数据的真实属性和分类预测结果类型之间的关系，是用来评价分类器性能的一种常用方法。混淆矩阵的每一列代表了预测类别，每一列的总数表示预测为该类别的数据的数目；每一行代表了数据的真实归属类别，每一行的数据总数表示该类别的数据实例的数目。

绘制混淆矩阵

def plot_confusion_matrix(cm, classes,normalize=False,title='Confusion matrix',cmap=plt.cm.Blues):
    """
    This function prints and plots the confusion matrix.
    Normalization can be applied by setting `normalize=True`.
    """
    if normalize:
        cm = cm.astype('float') / cm.sum(axis=1)[:, np.newaxis]
        print("Normalized confusion matrix")
    else:
        print('Confusion matrix, without normalization')
    print(cm)
    plt.imshow(cm, interpolation='nearest', cmap=cmap)
    plt.title(title)
    plt.colorbar()
    tick_marks = np.arange(len(classes))
    plt.xticks(tick_marks, classes, rotation=45)
    plt.yticks(tick_marks, classes)
    fmt = '.2f' if normalize else 'd'
    thresh = cm.max() / 2.
    for i, j in itertools.product(range(cm.shape[0]), range(cm.shape[1])):
        plt.text(j, i, format(cm[i, j], fmt),
                 horizontalalignment="center",
                 color="white" if cm[i, j] > thresh else "black")
    plt.tight_layout()
    plt.ylabel('True label')
    plt.xlabel('Predicted label')
    
cnf_matrix = confusion_matrix(date.flag, date.pred) #计算混淆矩阵
class_names = [0,1]
plt.figure()
plot_confusion_matrix(cnf_matrix, classes = class_names, title = 'Confusion matrix')  #绘制混淆矩阵
np.set_printoptions(precision=2)
print('Accary:', (cnf_matrix[1,1]+cnf_matrix[0,0])/(cnf_matrix[1,1]+cnf_matrix[0,1]+cnf_matrix[0,0]+cnf_matrix[1,0]))
print('Recall:', cnf_matrix[1,1]/(cnf_matrix[1,1]+cnf_matrix[1,0]))     
print('Precision:', cnf_matrix[1,1]/(cnf_matrix[1,1]+cnf_matrix[0,1]))  
print('Specificity:', cnf_matrix[0,0]/(cnf_matrix[0,1]+cnf_matrix[0,0]))
plt.show()

2.3 ROC（Receiver Operating Characteristic Curve）

受试者工作特征曲线（receiver operating characteristic curve，简称ROC曲线），又称为感受性曲线（sensitivity curve）。得此名的原因在于曲线上各点反映着相同的感受性，它们都是对同一信号刺激的反应，只不过是在几种不同的判定标准下所得的结果而已。它源于"二战"中用于敌机检测的雷达信号分析技术，二十世纪六七十年代开始被用于一些心理学、医学检测应用中，此后被引入机器学习领域。我们根据学习器的预测结果对样例进行排序，按此顺序逐个把样本作为正例进行预测，每次计算出两个重要量的值，分别以它们为横、纵坐标作图’就得到了 “ROC 曲线。。与 $P - R$ 曲线使用查准率、查全率为纵、横轴不同， ROC 曲线的纵轴是"真正例率” (True Positive Rate，简称 TPR)，横轴是"假正例率" (False PositiveRate，简称 FPR) 。ROC曲线的横坐标和纵坐标其实是没有相关性的，所以不能把ROC曲线当做一个函数曲线来分析，应该把ROC曲线看成无数个点，每个点都代表一个分类器，其横纵坐标表征了这个分类器的性能。为了更好的理解ROC曲线，我们先引入ROC空间，如下图所示

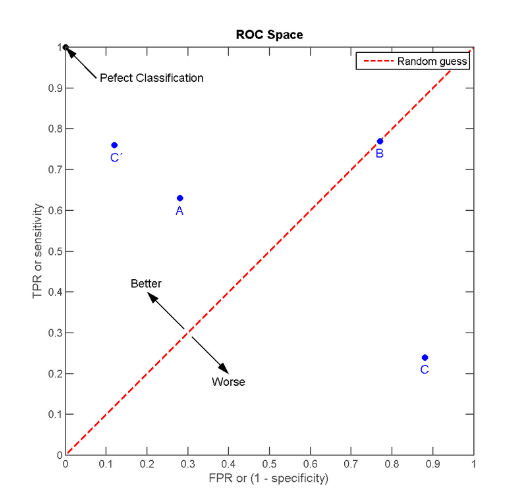
明显的，C’的性能最好。而B的准确率只有0.5，几乎是随机分类。特别的，图中左上角坐标为（1,0）的点为完美分类点（perfect classification），它代表所有的分类全部正确，即归为1的点全部正确（TPR=1），归为0的点没有错误（FPR=0）。

通过ROC空间，我们明白了一条ROC曲线其实代表了无数个分类器。那么我们为什么常常用一条ROC曲线来描述一个分类器呢？仔细观察ROC曲线，发现其都是上升的曲线（斜率大于0），且都通过点（0,0）和点（1,1）。其实，这些点代表着一个分类器在不同阈值下的分类效果，具体的，曲线从左往右可以认为是阈值从0到1的变化过程。当分类器阈值为0，代表不加以识别全部判断为0，此时TP=FP=0，TPR=TP/P=0，FPR=FR/N=0；当分类器阈值为1，代表不加以识别全部判断为1，此时FN=TN=0，P=TP+FN=TP, TPR=TP/P=1，N=FP+TN=FP, FPR=FR/N=1。所以，ROC曲线描述的其实是分类器性能随着分类器阈值的变化而变化的过程。

在现实任务中通常是利用有限个测试样例来绘制 ROC 图，此时仅能获得有限个(真正例率，假正例率)坐标对，画出的ROC曲线如下图：

当数据量足够大时，就能画出理想状态下的光滑曲线，如下图：

进行学习器的比较时，与 P-R 图相似，若一个学习器的 ROC 曲线被另一个学习器的曲线完全"包住"，则可断言后者的性能优于前者;若两个学习器的 ROC 曲线发生交叉，则难以-般性地断言两者孰优孰劣。此时如果一定要进行比较，则较为合理的判据是比较 ROC 曲线下的面积，即 AUC (Area UnderROC Curve)

2.4 AUC（Area Under ROC Curve）

AUC 的全称是 AreaUnderRoc 即 Roc 曲线与坐标轴形成的面积，取值范围 [0, 1]。AUC对所有可能的分类阈值的效果进行综合衡量，判断不同ROC曲线性能的好坏。

AUC的一般判断标准：

AUC = 1，是完美分类器，采用这个预测模型时，存在至少一个阈值能得出完美预测。绝大多数预测的场合，不存在完美分类器。
0.5 < AUC < 1，优于随机猜测。这个分类器（模型）妥善设定阈值的话，能有预测价值。
AUC = 0.5，跟随机猜测一样（例：丢铜板），模型没有预测价值。
AUC < 0.5，比随机猜测还差；但只要总是反预测而行，就优于随机猜测。

AUC特性：

AUC指标本身和模型预测score绝对值无关，只关注排序效果，因此特别适合排序业务。当然也会带来问题：

AUC 反应了太过笼统的信息。无法反应召回率、精确率等在实际业务中经常关心的指标。还有，AUC 的 misleading 的问题：modelA 和 modelB 的 ROC 曲线下面积 AUC 是相等的，但是两个模型在不同区域的预测能力是不相同的，所以我们不能单纯根据 AUC 的大小来判断模型的好坏。
AUC对分值本身不敏感，故常见的正负样本采样，并不会导致auc的变化。比如在点击率预估中，处于计算资源的考虑，有时候会对负样本做负采样，但由于采样完后并不影响正负样本的顺序分布。即假设采样是随机的，采样完成后，给定一条正样本，模型预测为score1，由于采样随机，则大于score1的负样本和小于score1的负样本的比例不会发生变化。但如果采样不是均匀的，比如采用word2vec的negative sample，其负样本更偏向于从热门样本中采样，则会发现auc值发生剧烈变化。
AUC非常适合评价样本不平衡中的分类器性能