POJ 2488 A Knight's Journey

最新推荐文章于 2023-01-31 11:15:00 发布

原创最新推荐文章于 2023-01-31 11:15:00 发布 · 631 阅读

0 ·

CC 4.0 BY-SA版权

002 算法竞赛专栏收录该内容

155 篇文章

订阅专栏

本文探讨了一个经典的计算机科学问题——骑士周游问题。该问题要求在一个缩小版的国际象棋棋盘上找到一条路径，使得骑士能够访问每一个方格恰好一次，并提供了一种使用深度优先搜索算法来解决这一问题的方法。

Description

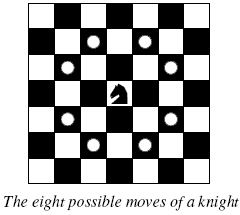Background
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans?

Problem
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number.
If no such path exist, you should output impossible on a single line.

Sample Input

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:

A1B3C1A2B4C2A3B1C3A4B2C4

题意：跟中国象棋马的走法一样，现在要求在国际象棋中让马走遍这个棋盘，如果能输出这个马走的路径，不能，则输出impossible。并且输出地格式要是字典序，而且输出按国际象棋棋盘的格式。所以我们要知道国际象棋横的是字母竖的是字母！

#include<stdio.h>
#include<string.h>
typedef struct point
{
        int x,y;        //位置x，y
}pp;
#define N 28
pp num[N],pur[N][N];        //num数组为输出这个路径，pur数组为了记录这个路径
int map[N][N],flag,p,q,ex,ey;   //map为标记数组
int dir[8][2]={-1,-2, 1,-2, -2,-1, 2,-1, -2,1, 2,1, -1,2, 1,2};
void DFS(int cx,int cy,int step)
{
    int i,kx,ky;
    if(step==p*q){  
          ex=cx;
          ey=cy;
          flag=1;
          return;
    }
    for(i=0;i<8;i++)
    {
               kx=cx+dir[i][0];
               ky=cy+dir[i][1];
               if(kx>=0&&kx<p&&ky>=0&&ky<q&&map[kx][ky]==0) //记录路径
                {
                       pur[kx][ky].x=cx;
                       pur[kx][ky].y=cy;
                       map[kx][ky]=1;
                       DFS(kx,ky,step+1);
                       if(flag)return;
                       map[kx][ky]=0;
                }
    }
}

int main()
{
        int n,i,j,k,path;
        scanf("%d",&n);
        for(k=1;k<=n;k++)
        {
            scanf("%d%d",&p,&q);
            memset(map,0,sizeof(map));
            map[0][0]=1;flag=0;
            DFS(0,0,1);
            printf("Scenario #%d:\n",k);
            if(flag==0)         //不能走完
                    printf("impossible\n");
            else{
                    i=ex;j=ey;path=1;
                    num[0].x=i;num[0].y=j;
                    while(i!=0||j!=0)       //为了输出路径
                    {
                        num[path].x=pur[i][j].x;
                        num[path].y=pur[i][j].y;
                        path++;
                        i=num[path-1].x;
                        j=num[path-1].y;
                    }
                    for(i=path-1;i>=0;i--)
                            printf("%c%d",num[i].y+'A',num[i].x+1);
                    printf("\n");
            }
            printf("\n");
        }
       return 0;
}