红黑树的原理与应用详解-优快云博客

本文链接：https://blog.youkuaiyun.com/u012173846/article/details/118736187

介绍与原理:

面试常问：什么是红黑树？_Mr.TS的博客-优快云博客_什么是红黑树

定义：

1.节点是红色或黑色。

2.根节点是黑色。

3.每个叶子节点都是黑色的空节点（NIL节点）。

4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

5.从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

这5个性质决定了从根节点到叶子节点的最长路径不可能大于最短路径的2倍。所以红黑树是一个大致平衡的二叉树。跟AVL树不同，红黑树并不是严格平衡的，而AVL树却是严格平衡的。

工程运用：

1.利用红黑树的特性，有序

2.用于快速查找，二分查找，c++中set/map就是使用的红黑树

具体：

linux进程调度CFS

Nginx Timer事件管理

Epoll事件块的管理

节点插入详情（三种情况）

1.当前节点的父节点是红色，且当前节点的叔节点也是红色

2.当前节点的父节点是红色，叔节点是黑色，且当前节点是其父节点的右孩子

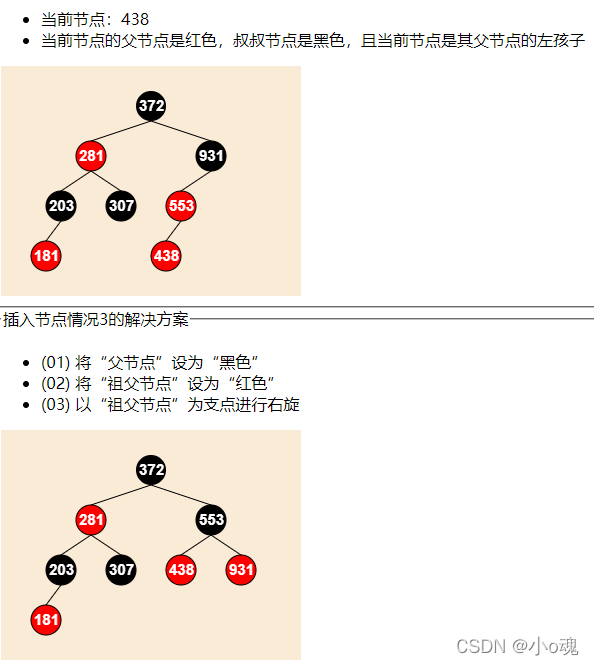
3.当前节点的父节点是红色，叔节点是黑色，且当前节点是其父节点的左孩子

插入数据的时候，是顺序插入

如何证明红黑树的的正确性？归纳法

插入一个新节点之前，当前节点永远是红色

情况一：

情况二：

情况三：

节点删除详情：

1. 当前结点的兄弟结点是红色的
2. 当前结点的兄弟结点是黑色的，而且兄弟结点的两个孩子结点都是黑色的
3. 当前结点的兄弟结点是黑色的，而且兄弟结点的左孩子是红色的，右孩子是黑色的。
4. 当前结点的兄弟结点是黑色的，而且兄弟结点的右孩子是红色的

情况一：

删除节点786

情况二：

删除节点62

情况三、情况四：

删除235

代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define RED				1
#define BLACK 			2

typedef int KEY_TYPE;

typedef struct _rbtree_node {
	unsigned char color;
	struct _rbtree_node *right;
	struct _rbtree_node *left;
	struct _rbtree_node *parent;
	KEY_TYPE key;
	void *value;
} rbtree_node;

typedef struct _rbtree {
	rbtree_node *root;
	rbtree_node *nil;
} rbtree;




rbtree_node *rbtree_mini(rbtree *T, rbtree_node *x) {
	while (x->left != T->nil) {
		x = x->left;
	}
	return x;
}

rbtree_node *rbtree_maxi(rbtree *T, rbtree_node *x) {
	while (x->right != T->nil) {
		x = x->right;
	}
	return x;
}


// 找后继
rbtree_node *rbtree_successor(rbtree *T, rbtree_node *x) {
	// 如果当前节点有子节点，后继就是右子树中的最小节点
	if (x->right != T->nil) {
		return rbtree_mini(T, x->right);
	}

	// 如果当前节点没有子节点，那后继就是父节点
	rbtree_node *y = x->parent;
	while ((y != T->nil) && (x == y->right)) {
		x = y;
		y = y->parent;
	}
	return y;
}




/* 左旋
 *	 x
 *	/ \
 * a   y
 *	  / \
 *	 b   c
 */
void rbtree_left_rotate(rbtree *T, rbtree_node *x) {
	// x = 当前节点，  y = 右子节点 
	// x  --> y  ,  y --> x,   right --> left,  left --> right
	rbtree_node *y = x->right;  

	x->right = y->left;					// 1  x-right = b
	if (y->left != T->nil) {
		y->left->parent = x;			// 2
	}

	y->parent = x->parent; 				// 3
	if (x->parent == T->nil) {   		// 4,x 是 root节点
		T->root = y;
	} else if (x == x->parent->left) {	// x是左子节点
		x->parent->left = y;
	} else {							// x是右子节点
		x->parent->right = y;
	}

	y->left = x; 						// 5
	x->parent = y; 						// 6
}


/* 右旋，跟左旋类似，就是代码反方向
 *	    y
 *	   / \
 *	  x   c
 *	 / \
 *	a   b
 */
void rbtree_right_rotate(rbtree *T, rbtree_node *y) {

	rbtree_node *x = y->left;

	y->left = x->right;
	if (x->right != T->nil) {
		x->right->parent = y;
	}

	x->parent = y->parent;
	if (y->parent == T->nil) {
		T->root = x;
	} else if (y == y->parent->right) {
		y->parent->right = x;
	} else {
		y->parent->left = x;
	}

	x->right = y;
	y->parent = x;
}


// 父子节点都为红色时调整
// z=当前节点，当前节点永远是红色的
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
	// 父子节点都为红色时调整
	while (z->parent->color == RED) { //z ---> RED
		if (z->parent == z->parent->parent->left) {
			rbtree_node *y = z->parent->parent->right;		// y=叔父节点
			if (y->color == RED) {							// 叔节点为红色的时候，只需要变换颜色，不需要旋转
				z->parent->color = BLACK;
				y->color = BLACK;
				z->parent->parent->color = RED;				// 将祖父节点设置为红色

				z = z->parent->parent; 						// 将当前节点设置为祖父节点
			} else {

				if (z == z->parent->right) {				// 当前节点是右子节点的情况
					z = z->parent;
					rbtree_left_rotate(T, z);
				}

				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rbtree_right_rotate(T, z->parent->parent);
			}
		}else {
			rbtree_node *y = z->parent->parent->left;
			if (y->color == RED) {
				z->parent->color = BLACK;
				y->color = BLACK;
				z->parent->parent->color = RED;

				z = z->parent->parent; //z --> RED
			} else {
				if (z == z->parent->left) {
					z = z->parent;
					rbtree_right_rotate(T, z);
				}

				z->parent->color = BLACK;
				z->parent->parent->color = RED;
				rbtree_left_rotate(T, z->parent->parent);
			}
		}
		
	}

	T->root->color = BLACK;
}

// 插入节点，跟二叉树插入类似
void rbtree_insert(rbtree *T, rbtree_node *z) {

	rbtree_node *y = T->nil;			// y = 在哪个节点下插入
	rbtree_node *x = T->root;

	while (x != T->nil) {				// 寻找插入点
		y = x;
		if (z->key < x->key) {			// left
			x = x->left;
		} else if (z->key > x->key) {	// right
			x = x->right;
		} else { 						// 键值已经存在则返回
			return ;
		}
	}

	z->parent = y;
	if (y == T->nil) {					// y是根节点的情况
		T->root = z;
	} else if (z->key < y->key) {		 
		y->left = z;
	} else {
		y->right = z;
	}

	z->left = T->nil;
	z->right = T->nil;
	z->color = RED;						// 颜色设置为红，红色不会影响整体高度，保持整体高度

	rbtree_insert_fixup(T, z);			// 插入调整
}



void rbtree_delete_fixup(rbtree *T, rbtree_node *x) {

	while ((x != T->root) && (x->color == BLACK)) {
		if (x == x->parent->left) {					// x是左子节点的情况

			rbtree_node *w= x->parent->right;		// 兄弟节点
			if (w->color == RED) {					// 兄弟节点如果是红色
				w->color = BLACK;					// 将兄弟节点变成黑色
				x->parent->color = RED;				// 并且将父节点变成红色

				rbtree_left_rotate(T, x->parent);	// 从父节点右转
				w = x->parent->right;
			}

			
			if ((w->left->color == BLACK) && (w->right->color == BLACK)) {	// 如果兄弟节点的子节点都是黑色
				w->color = RED;												// 将兄弟节点变成红色
				x = x->parent;
			} else {
				if (w->right->color == BLACK) {
					w->left->color = BLACK;
					w->color = RED;
					rbtree_right_rotate(T, w);
					w = x->parent->right;
				}

				w->color = x->parent->color;
				x->parent->color = BLACK;
				w->right->color = BLACK;
				rbtree_left_rotate(T, x->parent);

				x = T->root;
			}

		} else {

			rbtree_node *w = x->parent->left;
			if (w->color == RED) {
				w->color = BLACK;
				x->parent->color = RED;
				rbtree_right_rotate(T, x->parent);
				w = x->parent->left;
			}

			if ((w->left->color == BLACK) && (w->right->color == BLACK)) {
				w->color = RED;
				x = x->parent;
			} else {

				if (w->left->color == BLACK) {
					w->right->color = BLACK;
					w->color = RED;
					rbtree_left_rotate(T, w);
					w = x->parent->left;
				}

				w->color = x->parent->color;
				x->parent->color = BLACK;
				w->left->color = BLACK;
				rbtree_right_rotate(T, x->parent);

				x = T->root;
			}

		}
	}

	x->color = BLACK;
}

// 删除节点
// z=欲删除节点（当前节点）
rbtree_node *rbtree_delete(rbtree *T, rbtree_node *z) {

	rbtree_node *y = T->nil;		// 真正删除的节点
	rbtree_node *x = T->nil;		// 轴心节点

	if ((z->left == T->nil) || (z->right == T->nil)) {
		y = z;
	} else {
		y = rbtree_successor(T, z);		// 通过后继查找真正删除的节点
	}

	if (y->left != T->nil) {
		x = y->left;
	} else if (y->right != T->nil) {
		x = y->right;
	}

	x->parent = y->parent;
	if (y->parent == T->nil) {
		T->root = x;
	} else if (y == y->parent->left) {
		y->parent->left = x;
	} else {
		y->parent->right = x;
	}

	if (y != z) {
		z->key = y->key;
		z->value = y->value;
	}
	
	// 如果是黑色，整体高度发生了变化，需要做调整
	if (y->color == BLACK) {
		rbtree_delete_fixup(T, x);
	}

	return y;
}

rbtree_node *rbtree_search(rbtree *T, KEY_TYPE key) {

	rbtree_node *node = T->root;
	while (node != T->nil) {
		if (key < node->key) {
			node = node->left;
		} else if (key > node->key) {
			node = node->right;
		} else {
			return node;
		}	
	}
	return T->nil;
}


void rbtree_traversal(rbtree *T, rbtree_node *node) {
	if (node != T->nil) {
		rbtree_traversal(T, node->left);
		printf("key:%d, color:%d\n", node->key, node->color);
		rbtree_traversal(T, node->right);
	}
}

int main() {

	int keyArray[20] = {24,25,13,35,23, 26,67,47,38,98, 20,19,17,49,12, 21,9,18,14,15};

	rbtree *T = (rbtree *)malloc(sizeof(rbtree));
	if (T == NULL) {
		printf("malloc failed\n");
		return -1;
	}
	
	T->nil = (rbtree_node*)malloc(sizeof(rbtree_node));
	T->nil->color = BLACK;
	T->root = T->nil;

	rbtree_node *node = T->nil;
	int i = 0;
	for (i = 0;i < 20;i ++) {
		node = (rbtree_node*)malloc(sizeof(rbtree_node));
		node->key = keyArray[i];
		node->value = NULL;

		rbtree_insert(T, node);
		
	}

	rbtree_traversal(T, T->root);
	printf("----------------------------------------\n");

	for (i = 0;i < 20;i ++) {

		rbtree_node *node = rbtree_search(T, keyArray[i]);
		rbtree_node *cur = rbtree_delete(T, node);
		free(cur);

		rbtree_traversal(T, T->root);
		printf("----------------------------------------\n");
	}
	
}