Blocks
| Time Limit: 5000MS | Memory Limit: 65536K | |
| Total Submissions: 4318 | Accepted: 1745 |
Description
Some of you may have played a game called 'Blocks'. There are n blocks in a row, each box has a color. Here is an example: Gold, Silver, Silver, Silver, Silver, Bronze, Bronze, Bronze, Gold.
The corresponding picture will be as shown below:

Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.
Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.
Now let's look at the picture below:
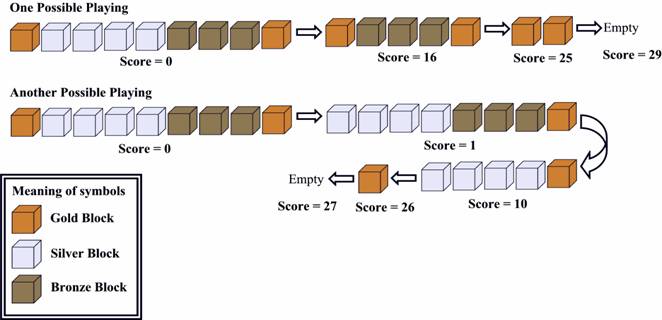
Figure 2
The first one is OPTIMAL.
Find the highest score you can get, given an initial state of this game.
The corresponding picture will be as shown below:

Figure 1
If some adjacent boxes are all of the same color, and both the box to its left(if it exists) and its right(if it exists) are of some other color, we call it a 'box segment'. There are 4 box segments. That is: gold, silver, bronze, gold. There are 1, 4, 3, 1 box(es) in the segments respectively.
Every time, you can click a box, then the whole segment containing that box DISAPPEARS. If that segment is composed of k boxes, you will get k*k points. for example, if you click on a silver box, the silver segment disappears, you got 4*4=16 points.
Now let's look at the picture below:

Figure 2
The first one is OPTIMAL.
Find the highest score you can get, given an initial state of this game.
Input
The first line contains the number of tests t(1<=t<=15). Each case contains two lines. The first line contains an integer n(1<=n<=200), the number of boxes. The second line contains n integers, representing the colors of each box. The integers are in the range
1~n.
Output
For each test case, print the case number and the highest possible score.
Sample Input
2 9 1 2 2 2 2 3 3 3 1 1 1
Sample Output
Case 1: 29 Case 2: 1
递归形式的动态规划:dp[st][ed][len]从st到ed完全消除,且ed右边挨着有一个len的大块颜色和ed相同.
一种消除方式是,Len块直接和ed块合并直接消除得到分数work(st,ed-1,0)+(a[ed].n+len)*(a[ed].n+len);
另一种是在st到ed之间找到一个块p和ed块颜色相同,把这3块直接合并 work(st,p,a[ed].n+len)+work(p+1,ed-1,0);
两种方式取最大的值。
当st==ed时递归结束。
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<stdlib.h>
#include<algorithm>
#include<queue>
using namespace std;
#define LL __int64
#define N 210
const int inf=0x1f1f1f1f;
struct node
{
int c,n,p;
}a[N];
int f[N][N][N];
int work(int st,int ed,int len)
{
if(f[st][ed][len])
return f[st][ed][len];
int i,ans=(a[ed].n+len)*(a[ed].n+len);
if(st==ed)
{
f[st][ed][len]=ans;
return ans;
}
ans+=work(st,ed-1,0);
for(i=ed-1;i>=st;i--)
{
if(a[i].c!=a[ed].c)
continue;
int tmp=work(st,i,a[ed].n+len)+work(i+1,ed-1,0);
if(tmp<=ans)
continue;
ans=tmp;
break;
}
f[st][ed][len]=ans;
return ans;
}
int main()
{
int T,t,cnt,i,n,Cas=1;
scanf("%d",&T);
while(T--)
{
memset(a,0,sizeof(a));
scanf("%d",&n);
scanf("%d",&t);
cnt=0;
a[cnt].c=t;
a[cnt].n=1;
for(i=1;i<n;i++)
{
scanf("%d",&t);
if(t==a[cnt].c)
{
a[cnt].n++;
}
else
{
cnt++;
a[cnt].c=t;
a[cnt].n=1;
}
}
memset(f,0,sizeof(f));
printf("Case %d: %d\n",Cas++,work(0,cnt,0));
}
return 0;
}





 本文探讨了在游戏开发过程中如何通过动态规划算法优化评分系统,实现高效的游戏体验提升。详细介绍了游戏内评分机制的设计原则,以及如何利用时间限制和内存限制等条件,通过最优路径选择算法提高玩家得分。实例分析了游戏内‘Blocks’环节的评分优化策略,包括点击操作、段落消除计分等关键要素,最终目标是为开发者提供实用的评分优化方法。
本文探讨了在游戏开发过程中如何通过动态规划算法优化评分系统,实现高效的游戏体验提升。详细介绍了游戏内评分机制的设计原则,以及如何利用时间限制和内存限制等条件,通过最优路径选择算法提高玩家得分。实例分析了游戏内‘Blocks’环节的评分优化策略,包括点击操作、段落消除计分等关键要素,最终目标是为开发者提供实用的评分优化方法。
















 1061
1061

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








