POJ 一 2488 A Knight's Journey（DFS）

A Knight's Journey

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 26133		Accepted: 8923

Description

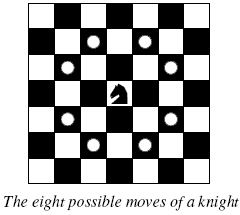
Background 
The knight is getting bored of seeing the same black and white squares again and again and has decided to make a journey 
around the world. Whenever a knight moves, it is two squares in one direction and one square perpendicular to this. The world of a knight is the chessboard he is living on. Our knight lives on a chessboard that has a smaller area than a regular 8 * 8 board, but it is still rectangular. Can you help this adventurous knight to make travel plans? 

Problem 
Find a path such that the knight visits every square once. The knight can start and end on any square of the board.

Input

The input begins with a positive integer n in the first line. The following lines contain n test cases. Each test case consists of a single line with two positive integers p and q, such that 1 <= p * q <= 26. This represents a p * q chessboard, where p describes how many different square numbers 1, . . . , p exist, q describes how many different square letters exist. These are the first q letters of the Latin alphabet: A, . . .

Output

The output for every scenario begins with a line containing "Scenario #i:", where i is the number of the scenario starting at 1. Then print a single line containing the lexicographically first path that visits all squares of the chessboard with knight moves followed by an empty line. The path should be given on a single line by concatenating the names of the visited squares. Each square name consists of a capital letter followed by a number. 
If no such path exist, you should output impossible on a single line.

Sample Input

3
1 1
2 3
4 3

Sample Output

Scenario #1:
A1

Scenario #2:
impossible

Scenario #3:
A1B3C1A2B4C2A3B1C3A4B2C4

题意是国际象棋中的马按照图示方法走，对给定大小的棋盘，判断能否走完棋盘，若能输出走的路径，不能输出possible

用DFS做，依次检查每个点，判断最终步数step是否等于棋盘大小p*q;

用dir[][]二维数组来表示马的下一步走向，简化了操作。

代码如下：

<pre code_snippet_id="288901" snippet_file_name="blog_20140412_7_9349528" name="code" class="cpp">#include<stdio.h>
#define max 27

int p,q,sign,step;
int map[max][max];//用map数组的值判断某个点是否遍历过 
int sx[max],sy[max];//用这两个数组记录某点的坐标 
int dir[8][2]={{-2,-1},{-2,1},{-1,-2},{-1,2},{1,-2},{1,2},{2,-1},{2,1}};//二维数组用于移动表示 

void dfs(int i,int j);

int main(void)
{
    int t,j,i,n;
    scanf("%d",&n);
    t=1;
    while(n--)
    {
     sign=0;//用sign标志判断是否完成所有遍历 
     step=0;//记录当前遍历点的个数 
     scanf("%d%d",&p,&q);
     for(i=1;i<=p;i++)
     {
      for(j=1;j<=q;j++)
      map[i][j]=0;//将所有点置为未遍历状态   
     }
     dfs(1,1);
     printf("Scenario #%d:\n",t++);          
     if(sign)
     {
      for(i=1;i<=p*q;i++)
      printf("%c%d",sy[i]+64,sx[i]);
      printf("\n");
     }
     else
     printf("impossible\n");
     if(n)
     printf("\n");    
    }
    return 0;
} 

void dfs(int i,int j)
{
     int k,x,y;
     
     if(sign)
     return ;
     step++;
     sx[step]=i;
     sy[step]=j;
     if(step==p*q)
     {
      sign=1;
      return;             
     }
     map[i][j]=1;
     for(k=0;k<8;k++)
     {
      x=i+dir[k][1];
      y=j+dir[k][0];//重新记录当前点的坐标 
      if(map[x][y]==0 && x>0 && x<=p && y>0 && y<=q)
      {
       dfs(x,y);//判断当前点为未遍历点，从这点开始dfs 
       step--;//退出当前对该分支的遍历 
      }            
     }
     map[i][j]=0;
}