随机数据扩充

引言

数据扩充加密（也可称为插值）是比较常见的数据操作，确定性数据的扩充比较简单，可以使用各种插值算法，如线性插值、拉格朗日插值、样条插值等等等；而当数据是随机的时候，有时候也需要插值加密，但比确定性情况复杂的多。
蒙特卡洛模拟中经常需要生成大量满足要求分布的数据，一般有两种方法：已知分布参数情况下，直接生成大量满足要求分布的数据；已知分布形式情况下，由少量数据生成大量数据，也可称为扩充加密。本文从一维到二维，分别探讨了通过少量数据生成同分布大量数据的算法，最后给出了Matlab代码供感兴趣的朋友尝试。

1 一维情况

基本理论

定义：若数据的平均值为，方差为$s^2$，则新数据的平均值为，方差为。反之，若$X$表示均值为$\mu$方差为$\sigma$的随机数序列，则方差为$a\sigma$均值为$\mu +b$的随机数序列$Y$可以表示为：

$$Y=\sqrt{a}X+b\text{\hspace{1em}(1)}$$

以上公式也表明，只需有一组正态分布随机数，公式(1)可以用于生成特定标准差和均值的正态分布随机数。

利用标准正态分布数据生成非标准正态分布数据

若有少量假定满足（非标准）正态分布的n维初始随机数向量$X$，要求扩充成大量$m$维同分布的随机数向量$Y$，则可以使用以下的扩充公式。

$$Y=\sqrt{\frac{1}{n}\sum _{i=1}^n\left(x_i-\bar{x}\right)}\times U+\bar{x}\text{\hspace{1em}(2)}$$

其中，第一项是初始数据的标准差估计；第二项$U$是满足标准正态分布的$m$维随机数向量；第三项是均值估计。

2 二维情况

基本理论

一维数据可以表示为某条直线上的一系列点，只需要一列数据就可以唯一确定这些点的位置。

二维数据可以表示为二维平面上的一系列点，需要两列数据（$x$坐标和$y$坐标）才能唯一确定这些点的位置。

二维和一维的不同点在于，多了用于衡量两个维度相关性的协方差，我们需要关心$x$的变化会不会使$y$产生相应的变化。因此，在二维情况中引入公式(3)所示的协方差矩阵来衡量两个维度的相关性：

$$\Sigma =\left[\begin{array}{cc}Cov\left(X,X\right)& Cov\left(X,Y\right)\\ Cov\left(Y,X\right)& Cov\left(Y,Y\right)\end{array}\right]\text{\hspace{1em}(3)}$$

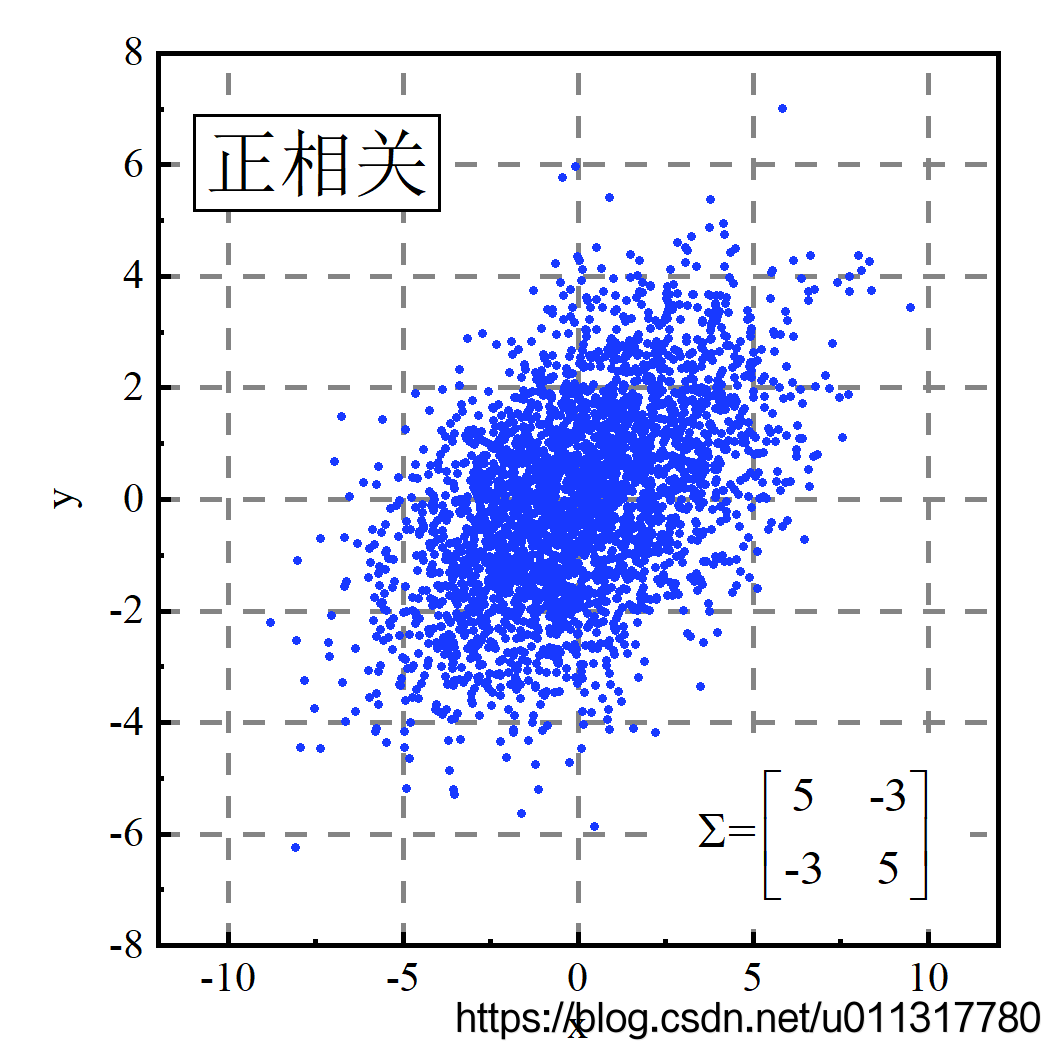
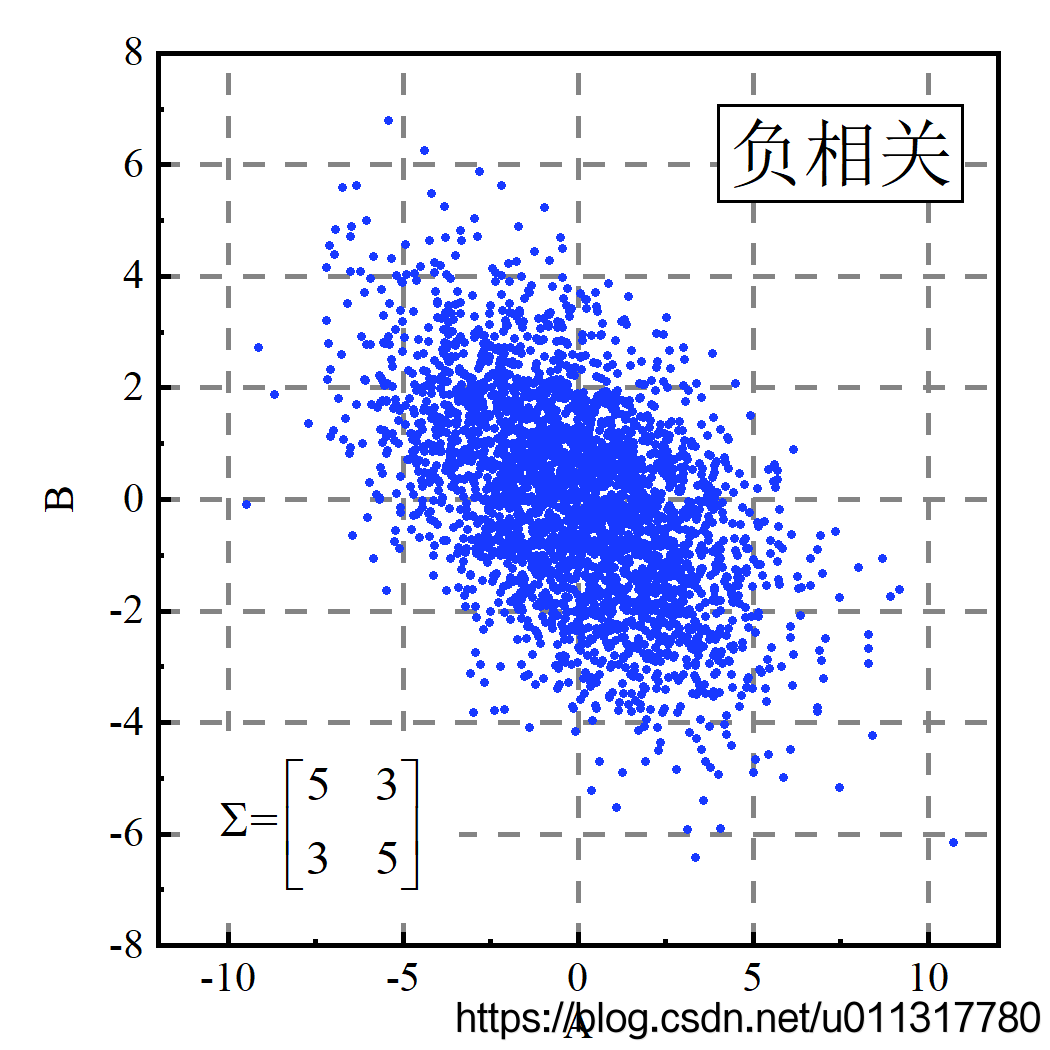
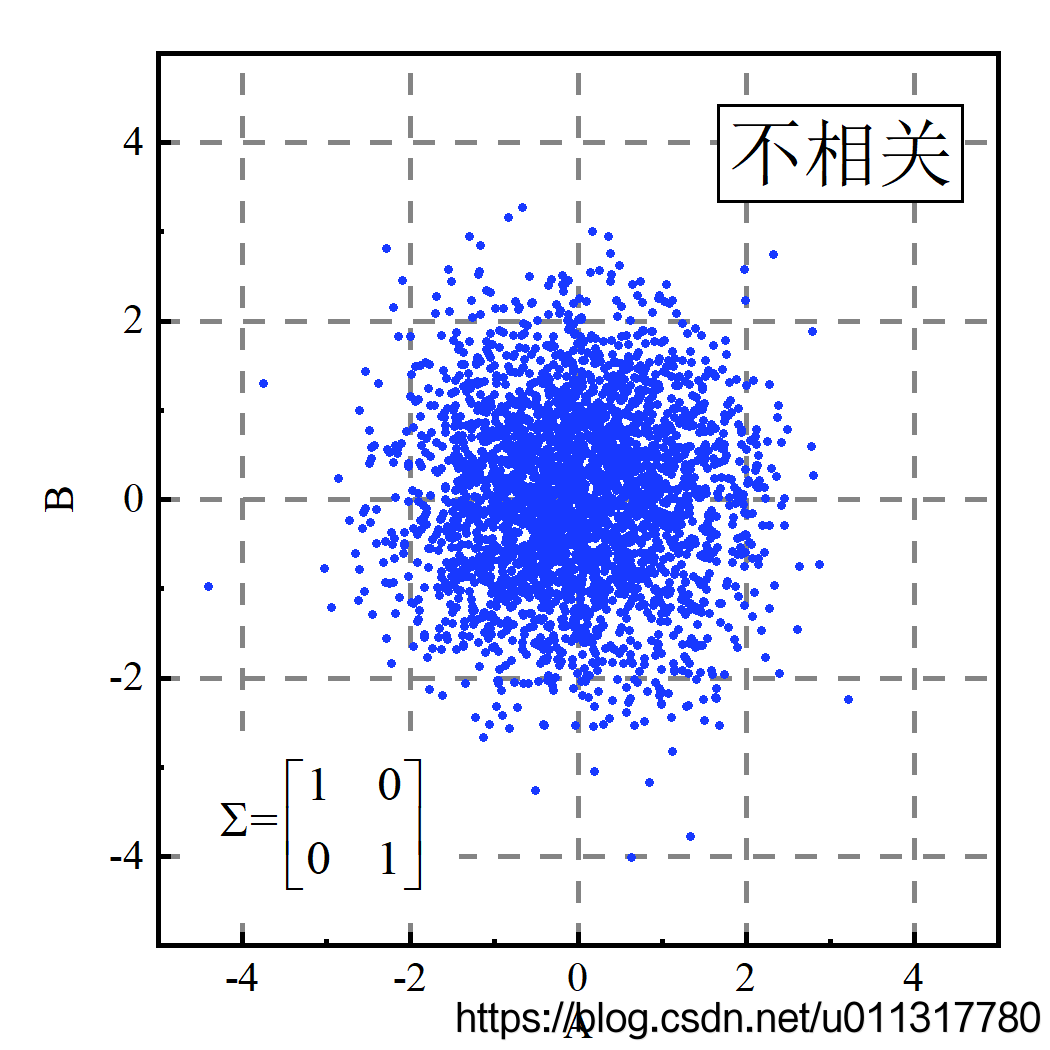
协方差矩阵中的主对角线是对应变量的方差，斜对角线是两个变量的协方差。从图中可以看到，当协方差为正时，两个维度正相关，表现为y具有随x的增大而增大的趋势；当协方差为负时，两个维度负相关，表现为$y$具有随$x$的增大而减小的趋势；当协方差为零时，两变量不相关，$y$随$x$的变化没有明显的变化趋势。

利用标准正态分布数据生成非标准正态分布数据

若有相互独立的标准正态分布变量$X$和$Y$，及其线性组合后的随机变量$A=aX+bY$和$B=cX+$