数据结构与算法三： 数组

前言

知识让生活更具能量。希望我们在以后学习的路上携手同行。您的点赞、评论和打赏都是对我最大的鼓励。一个人能走多远要看与谁同行，希望能与优秀的您结交。

首先我们先来介绍一下数组

数组（Array)是一种线性表 数据结构。它用一组连续的内存空间，来存储一组具有相同类型的数据。
上面是对数组这种数据结构的定义，下面我们来解释一下里面几个关键的词。

1. 线性表： 线性表的数据就像一条线一样。每个线性表上的数据最多只有前和后两个方向。链表，队列，栈都是线性表结构。
   
   与线性表相对应的是非线性表结构
   
2. 第二个是连续的内存空间和相同类型的数据。这两个限制，让数据的查询速度快，也就是“随机访问”， 但是会让数组在插入和删除数据的时候速度变慢。

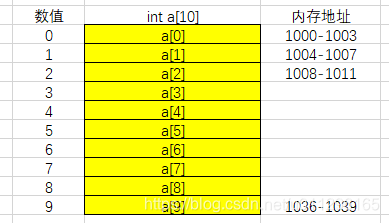
这个图表示，定义了一个长度为10的数组。分配了一块连续的内存空间1000-1039。base_adress为1000。
当计算机想要找某个值时，就会通过下面这个公式来查询：
value = base_adress+i*data_type_size
data_type_size表示数组中每个元素的大小。这在个公式中data_type_size为4.因为数组中存储的值为int类型， int类型占用空间为4个字节。

数组插入和删除分析

假设我们有一个数组，长度为n。现在我们将一个数据添加到第C个位置。（哈哈 ，没错，谁都想占C位） 为了把C位腾出来，就需要把从C到N位的数据都往后顺位移动一位。 可以想象一下排队买火车票，中间有一个人加塞了，是不是后面的所有人都要往后靠一位呢！（鄙视这种行为）

大家还记得前面我们一起学习的时间复杂度分析吗？
如果在数组的末尾插入元素，那就不需要移动数据了，所以最好时间复杂度为O(1)。
如果在数组的开头插入数据，那么所有数据都要往后移动一位，因此最坏时间复杂度为O(n)。
因为我们在每个位置插入数据的概率是一样的，就把每种情况需要做的操作做为分子，把所有情况做为分母 所以平均时间复杂度为$\frac{(1+2+3+.....+n)}{n}$=O(n)。
这也就是我们经常所说的数据插入数据的时候效率低。因为会随着数据量的增长，插入数据的时间也会增长。
为什么要用这种方式来维护数据呢？ 这里我们要特别注意一点的是的value = base_adress+i*data_type_size 这个公式。 我们在查询数组值的时候需要运用这个公式来查询值。
所以在程序代码中比如java中， 如果要给数组插入数据的时候，要移动数据其实就是重新计算一下地址值。

但是如果我们打破数组第二条限制条件：连续的内存空间 系统在插入数据的时候也就没有必要在去维护连续的地址值了。插入数据的的过程就可以变成下面这种形式。
如果要将某个数组插入到第C个位置，为了避免大规模的数据搬移，我们可以直接将C位的数据搬移到数组元素的最后，把新数据直接放置到C位上。

这样速度 是不是就快很多呢？ 但是我们java程序中的数组并不是这么设计的。大家在回看一下这个公式value = base_adress+i*data_type_size。 如果随意移动数据值，而不去维护数组中数据的地址值那么我们在使用这个公式的时候还能不能取出结果来呢？取出的结果就不正确了。

跟插入类似，如果删除数组末尾的数据，则最好情况时间复杂度为O(1); 如果删除开头数据则时间复杂度为O(n)。平均情况时间复杂度为O(n)。

那么现在我们忘记地址值这个事情，只是单纯的处理一个数组，如果我删除数据的时候，是不是可以考虑将多次要删除的数据集中在一起，一起执行。
看下面这个例子： 我们有一个数组，我们要依次删除 a,b,c这三个值 。

为了避免d,e,f这几个数据被搬移三次，我们可以先记录下已经删除的数据。当数组没有更多空间的时候，我们在触发一次性执行删除操作。这种操作也被jvm标记清除垃圾回收算法的核心思想。

分析一下java语言中ArrayList和数组的优劣

首先要知道的是ArrayList是对数组的封装。数组在定义的时候需要指定大小，因为需要分配连续的内存空间。如果申请了大小为10的数组，当第11个数据需要存储到数组中时，我们就需要分配一块更大的空间，将原来的的数据复制过去 ，然后再将新的数据插入。

ArrayList对数组的这种扩容进行了封装，第次存储空间不足的时候，就会扩大到原来的1.5倍。因为扩容比较耗时，最好在创建ArrayList的时候先指定数据的大小。

1. ArrayList无法存储基础类型，如果需要存储基础类型，就需要使用数组。
2. 像一些中间件，脱离业务场景并对性能要求很高的要用数组。
3. 不考虑性能的话ArrayList是首选 ！！！

喜欢我的文章，请关注公众号吧。 我们做个朋友，一起进步。