堆排序

一. 堆

堆排序是完全二叉树的应用，是充分利用完全二叉树的一种选择特性。最小堆，根节点最小；最大堆，根节点最大。

利用堆求最大或最小的前k个数：用堆在海量数据中找出最大或最小的k个数，效率非常高。

a.将无序列的数据构建成一个无序的堆，根据升序或降序需求初始化一个大顶堆或者小顶堆

b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

c.重新调整结构，使其满足堆定义（最大堆，最小堆），然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

二. 原理详解

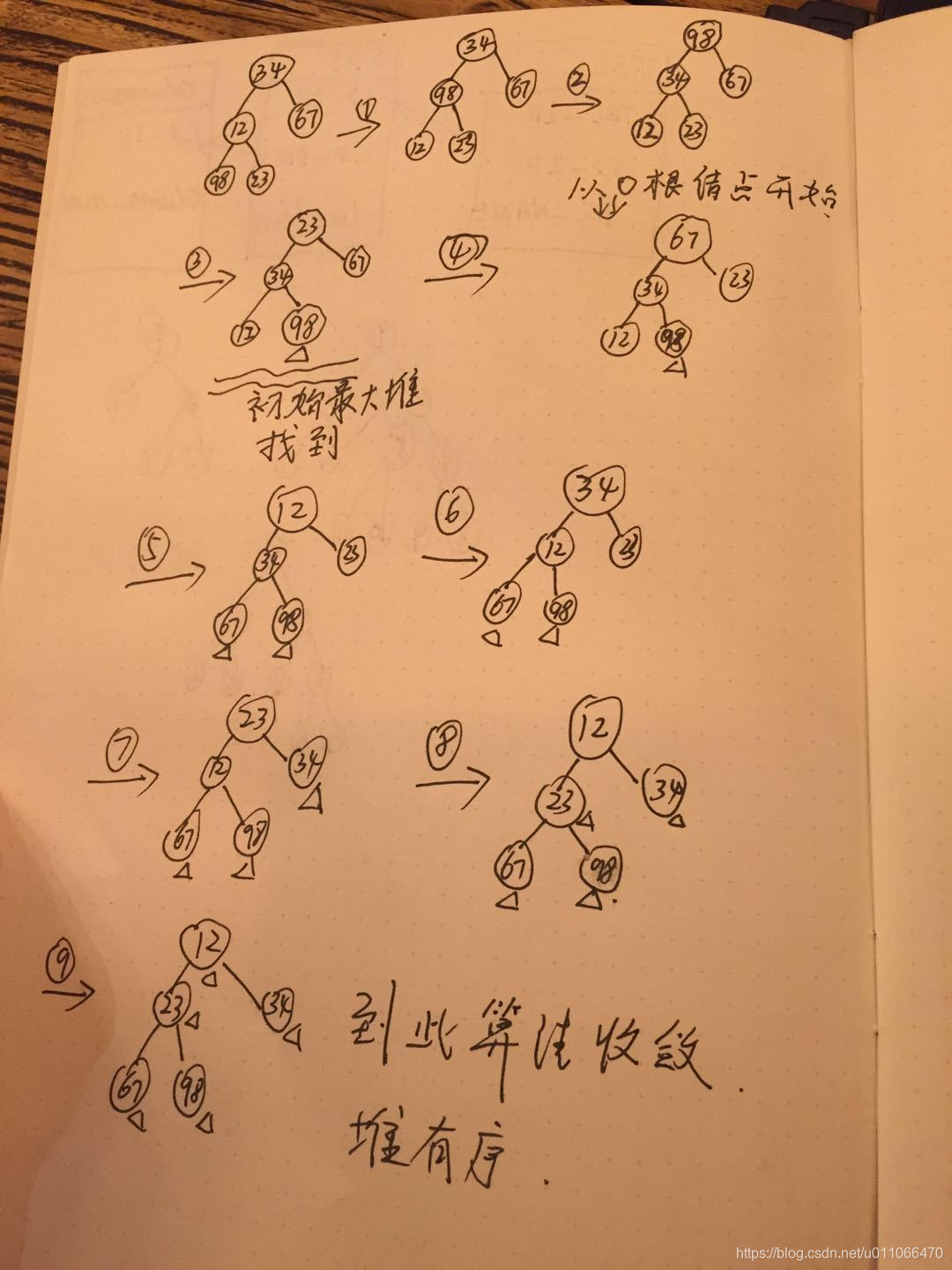
https://www.cnblogs.com/chengxiao/p/6129630.htm

三.代码

public class App 
{
    public static void main( String[] args )
    {
       int a[]={34,12,67,98,23};
        heapSort(a);
    System.out.println("sort:"+ Arrays.toString(a));
    }
    public static void heapSort(int a[]){
        //初始化最大堆顶
        for(int k=a.length/2-1;k>=0;k--){//左边一条;注意k必须包含=0；
            switchData( a,k,a.length);
        }
        //交换堆顶和叶子
        for(int j=a.length-1;j>=0;j--){//从0开始进行比对
            sweapData( a,0,j);
            switchData( a,0,j);
        }
    }
    public static void switchData(int a[],int i,int length){
        int temp=a[i];//每个父节点的左边孩子
        //比较父节点的左右两个孩子是否比它大；
        for(int k=2*i+1;k<length;k=2*k+1){//左边孩子的孩子
            //左右两个节点自我比较一下，让大的节点和父节点进行比较，右边大的话，指针向右边移动一下。
            if(k+1<length&&a[k+1]>a[k]){//右边节点大于左边，k 右边移动
                k++;
            }
            if(a[k]>temp){//孩子节点大于父节点
                a[i]=a[k];//将孩子节点的值赋值给父节点
                i=k;//将孩子节点的坐标，赋值给父节点，使指向为孩子节点的位置
            }
            else{
                break;
            }
        }
        a[i]=temp;
    }
    public static void sweapData(int a[],int m,int n){
        int temp=a[m];
        a[m]=a[n];
        a[n]=temp;
    }
}

四.结果

sort:[12, 23, 34, 67, 98]
 

都看到这里了，就顺手点击左上角的【关注】按钮，点击右上角的小手，给个评论，关注一下，再走呗！☺