hdu 4498 Function Curve（分段曲线积分）

最新推荐文章于 2023-11-24 22:55:56 发布

原创最新推荐文章于 2023-11-24 22:55:56 发布 · 1k 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#ACM #积分 #数学 #hdu 4498

ACM之路（c/c++）同时被 3 个专栏收录

227 篇文章

订阅专栏

计算几何

44 篇文章

订阅专栏

数学

42 篇文章

订阅专栏

本文介绍了一种计算特定函数在指定区间内曲线长度的方法。通过找到函数的所有交点，并将其转换为分段函数，利用辛普森法则进行数值积分来近似计算曲线长度。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Function Curve

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65535/65535 K (Java/Others)
Total Submission(s): 249 Accepted Submission(s): 93

Problem Description

Given sequences of k ₁, k ₂, … k _n, a ₁, a ₂, …, a _n and b ₁, b ₂, …, b _n. Consider following function:

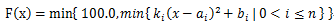
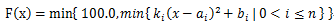
Then we draw F(x) on a xy-plane, the value of x is in the range of [0,100]. Of course, we can get a curve from that plane.
Can you calculate the length of this curve？

Input

The first line of the input contains one integer T (1<=T<=15), representing the number of test cases.
Then T blocks follow, which describe different test cases.
The first line of a block contains an integer n ( 1 <= n <= 50 ).
Then followed by n lines, each line contains three integers k _i, a _i, b _i ( 0<=a _i, b _i<100, 0<k _i<100 ) .

Output

For each test case, output a real number L which is rounded to 2 digits after the decimal point, means the length of the curve.

Sample Input

Sample Output

  
   215.56 
278.91 

   
    
     Hint
    
All test cases are generated randomly.

Source

2013 ACM-ICPC吉林通化全国邀请赛——题目重现

题意：求上函数的0~100区间的曲线段的长度

题解：求出所有函数交点x坐标，将函数变成分段函数，然后对每一段求曲线积分就行了。。。可是曲线积分有点难求（对于我）。。。所以simpson一下，year~

注意交点貌似挺多的，至少大于333个。。。我开始就拼命RE这里，另外simpson也TLE了一下。。还是挺靠感觉调的

#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#define eps 1e-8
double a[53],b[53],k[53],point[33333];
int all,n,id;
int cmp(const void *a,const void *b)
{
    return *(double *)a<*(double *)b?-1:1;
}
double Function(double x,int id)
{
    return k[id]*(x-a[id])*(x-a[id])+b[id];
}
double Func(double x)
{
    return sqrt(1+(2*k[id]*(x-a[id]))*(2*k[id]*(x-a[id])));
}
double simpson(double l,double r)
{
    double mid=(l+r)/2.0;
    return (r-l)*(Func(l)+4*Func(mid)+Func(r))/6.0;
}
double cal(double l,double r,double all)
{
    double mid=(l+r)/2.0;
    double L=simpson(l,mid);
    double R=simpson(mid,r);
    if(fabs(L+R-all)<=eps) return all;
    else return cal(l,mid,L)+cal(mid,r,R);
}
void get_point()
{
    int i,j;
    double x1,x2,aa,bb,cc;

    for(i=0;i<n;i++)
    {
        if(b[i]>100) continue;
        x1=sqrt((100-b[i])/k[i])+a[i];
        x2=-sqrt((100-b[i])/k[i])+a[i];
        if(-eps<x1&&x1<100+eps) point[all++]=x1;
        if(-eps<x2&&x2<100+eps) point[all++]=x2;
    }
    for(i=0;i<n;i++)
    {
        for(j=i+1;j<n;j++)
        {
            aa=k[i]-k[j];
            bb=-2*a[i]*k[i]+2*a[j]*k[j];
            cc=a[i]*a[i]*k[i]+b[i]-a[j]*a[j]*k[j]-b[j];
            if(bb*bb-4*aa*cc<0) continue;
            x1=(sqrt(bb*bb-4*aa*cc)-bb)/(2*aa);
            x2=(-sqrt(bb*bb-4*aa*cc)-bb)/(2*aa);
            if(0<x1&&x1<100) point[all++]=x1;
            if(0<x2&&x2<100) point[all++]=x2;
        }
    }
}
int main()
{
    int t,i,j;
    double left,right,mid,res;

    //freopen("t.txt","r",stdin);
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        for(i=0;i<n;i++) scanf("%lf%lf%lf",k+i,a+i,b+i);
        all=0,point[all++]=0,point[all++]=100;
        get_point();
        qsort(point,all,sizeof(point[0]),cmp);
        for(res=i=0;i<all-1;i++)
        {
            left=point[i],right=point[i+1];
            mid=(left+right)/2;

            if(right-left<eps) continue;
            id=0;
            for(j=1;j<n;j++)
            {
                if(Function(mid,j)-Function(mid,id)<0) id=j;
            }
            if(Function(mid,id)-100<0)
                res+=cal(left,right,simpson(left,right));
            else res+=right-left;
        }
        printf("%.2lf\n",res);
    }

    return 0;
}