机器学习6

10 Advice for Applying Machine Learning

10.1 Deciding What to Try Next

仍然使用预测房价的学习例子，假如你已经完成了正则化线性回归，也就是最小化
代价函数 J 的值，假如，在你得到你的学习参数以后，如果你要将你的假设函数放到一组新的房屋样本上进行测试，假如说你发现在预测房价时产生了巨大的误差，现在你的问题是要想改进这个算法，接下来应该怎么办？

1. 获得更多的训练实例——通常是有效的，但代价较大，下面的方法也可能有效，可
   考虑先采用下面的几种方法。
2. 尝试减少特征的数量;有一系列特征比如 x1x2 x3等等，从这些特征中仔细挑选一小部分来防止过拟合。或者也许你需要用更多的特征，从获取更多特征的角度来收集更多的数据。
3. 尝试获得更多的特征
4. 尝试增加多项式特征;比如 x1的平方， x2的平方， x1x2的乘积。
5. 尝试减少归一化程度 λ
6. 尝试增加归一化程度 λ

>“机器学习诊断法”。
这是一种测试法， 你通过执行这种测试， 能够深入了解某种算法到底是否有用。 这通常也能够告诉你， 要想改进一种算法的效果， 什么样的尝试， 才是有意义的。

10.2 Evaluating a Hypothesis

选择参量来使训练误差最小化，但仅仅是因为这个假设具有很小的训练误差，并不能说明它就一定是一个好的假设函数。过拟合假设函数推广到新的训练集上是不适用的。
如何判断一个假设函数是过拟合的呢？
为了检验算法是否过拟合，我们将数据分成训练集和测试集，通常用 70%的数据作为训
练集，用剩下 30%的数据作为测试集。很重要的一点是训练集和测试集均要含有各种类型的数据，通常我们要对数据进行“洗牌”，然后再分成训练集和测试集
测试集评估在通过训练集让我们的模型学习得出其参数后，对测试集运用该模型，我们
有两种方式计算误差：

1. 对于线性回归模型，我们利用测试集数据计算代价函数 J
2. 对于逻辑回归模型，我们除了可以利用测试数据集来计算代价函数外：
   
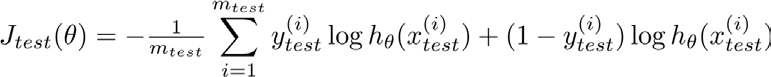
   还能计算错误分类的比例，对每一个测试集计算如下：

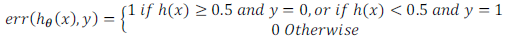
最后对计算结构求平均。

---

10.3 Model Selection and Train/Validation/Test Sets

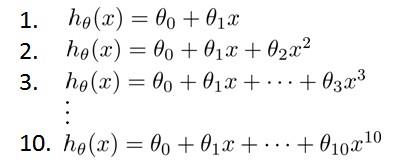
显然越高次数的多项式模型越能够适应我们的训练数据集，但是适应训练数据集并不代
表着能推广至一般情况，我们应该选择一个更能适应一般情况的模型。我们需要使用交叉验证集来帮助选择模型。
即：使用 60%的数据作为训练集， 使用 20%的数据作为交叉验证集， 使用 20%的数据
作为测试集。
模型选择的方法为：

1. 使用训练集训练出 10 个模型
2. 用 10 个模型分别对交叉验证集计算得出交叉验证误差（代价函数的值）
3. 选取代价函数值最小的模型
4. 用步骤 3 中选出的模型对测试集计算得出推广误差（代价函数的值）
   

---

10.4 Diagnosing Bias(偏差) vs. Variance（方差）

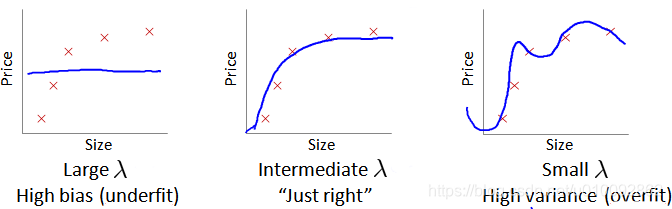
如果算法的表现不理想，主要是两种情况：要么是偏差比较大，要么是方差比较大。换句话说，出现的情况要么是欠拟合，要么是过拟合。 高偏差和高方差的问题基本上来说是欠拟合和过拟合的问题。

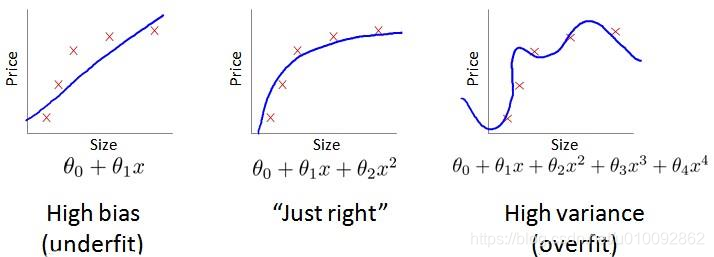
我们通常会通过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析：


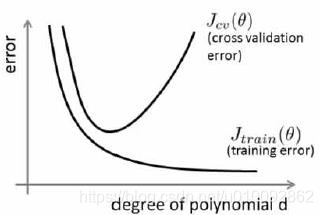
对于训练集，当 d (degree of polynomial 多项式次数)较小时，模型拟合程度更低，误差较大；随着 d 的增长，拟合程度提
高，误差减小。
对于交叉验证集，当 d 较小时，模型拟合程度低，误差较大；但是随着 d 的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。如果我们的交叉验证集误差较大，我们如何判断是方差还是偏差呢？ 根据上面的图表，我们知道:

训练集误差和交叉验证集误差近似时： 偏差/欠拟合
交叉验证集误差远大于训练集误差时： 方差/过拟合

---

10.5 Regularization and Bias/Variance

归一化 Normalization
归一化一般是将数据映射到指定的范围，用于去除不同维度数据的量纲以及量纲单位。常见的映射范围有 [0, 1] 和 [-1, 1] ，最常见的归一化方法就是 Min-Max 归一化：
Min-Max 归一化

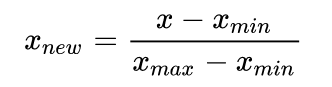
当x两个值相差很大时，超大的数就会起到主导作用从而遮盖住其他的特征，归一化后就不会有这样的问题。 但是 我们前面讨论文均值归一化，是下面的标准化 方法。。

标准化 Normalization
归一化和标准化的英文翻译是一致的，但是根据其用途（或公式）的不同去理解（或翻译）。下面我们将探讨最常见的标准化方法： Z-Score 标准化。
在这里插入图片描述

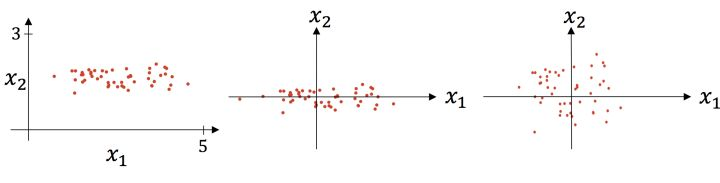
上图则是一个散点序列的标准化过程：原图->减去均值->除以标准差。

显而易见，变成了一个均值为 0 ，方差为 1 的分布，下图通过 Cost 函数让我们更好的理解标准化的作用。

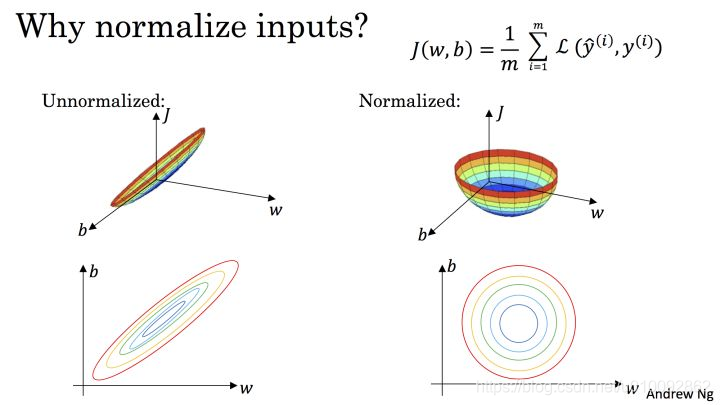
机器学习的目标无非就是不断优化代价函数，使其值最小。在上图中， J(w,b) 就是我们要优化的目标函数

我们不难看出，标准化后可以更加容易地得出最优参数 w 和 b 以及计算出 J(w,b) 的最小值，从而达到加速收敛的效果。

Batch Normalization
在机器学习中，最常用标准化的地方莫过于神经网络的 BN 层（Batch Normalization），因此我们简单的谈谈 BN 层的原理和作用。我们知道数据预处理做标准化可以加速收敛，同理，在神经网络使用标准化也可以加速收敛，而且还有如下好处：

• 具有正则化的效果（Batch Normalization reglarizes the model）
• 提高模型的泛化能力（Be advantageous to the generalization of network）
• 允许更高的学习速率从而加速收敛（Batch Normalization enables higher learning rates）
• 其原理是利用正则化减少内部相关变量分布的偏移（Reducing Internal Covariate Shift），从而提高了算法的鲁棒性。
  Batch Normalization 由两部分组成，第一部分是缩放与平移（scale and shift），第二部分是训练缩放尺度和平移的参数（train a BN Network）。

** 正则化 Regularization**
正则化主要用于避免过拟合的产生和减少网络误差。正则化一般具有如下形式：

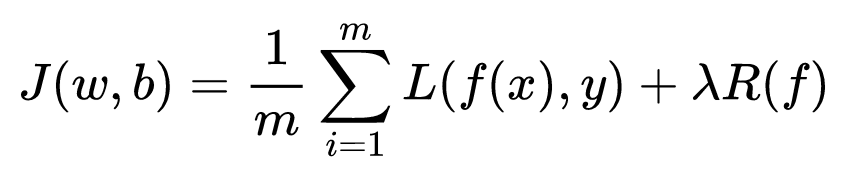
其中，第 1 项是经验风险，第 2 项是正则项， λ≥0 为调整两者之间关系的系数。第 1 项的经验风险较小的模型可能较复杂（有多个非零参数），这时第 2 项的模型复杂度会较大。常见的有正则项有 L1 正则 和 L2 正则 ，其中 L2 正则 的控制过拟合的效果比 L1 正则 的好。正则化的作用是选择经验风险与模型复杂度同时较小的模型。常见的有正则项有 L1 正则 和 L2 正则 以及 Dropout ，其中 L2 正则 的控制过拟合的效果比 L1 正则 的好。

在我们在训练模型的过程中，一般会使用正则化方法来防止过拟合。但是我们可能会正则化的程度太高或太小了，即我们在选择 λ 的值时也需要思考与刚才选择多项式模型次数类似的问题。

我们选择一系列的想要测试的 λ 值，通常是 0-10 之间的呈现 2 倍关系的值（0,0.01,0.02,0.04,0.08,0.15,0.32,0.64,1.28,2.56,5.12,10 共 12 个）。

选择 λ 的方法为：

1. 使用训练集训练出 12 个不同程度归一化的模型
2. 用 12 模型分别对交叉验证集计算的出交叉验证误差
3. 选择得出交叉验证误差最小的模型
4. 运用步骤 3 中选出模型对测试集计算得出推广误差， 我们也可以同时将训练集和交叉验证集模型的代价函数误差与 λ 的值绘制在一张图表上：
   

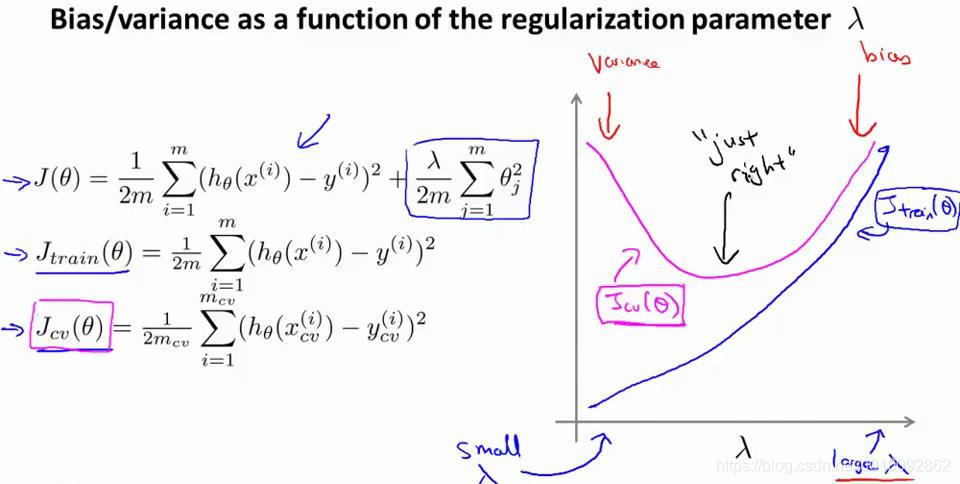
• 当 λ 较小时，训练集误差较小（过拟合）而交叉验证集误差较大
• 随着 λ 的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加.

---

10.6 Learning Curves

使用学习曲线来判断某一个学习算法是否处于偏差、方差问题。 学习曲线是学习算法的一个很好的合理检验（sanity check）。学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量（m）的函数绘制的图表。即，如果我们有 100 行数据，我们从 1 行数据开始，逐渐学习更多行的数据。思想是：当训练较少行数据的时候，训练的模型将能够非常完美地适应较少的训练数据，但是训练出来的模型却不能很好地适应交叉验证集数据或测试集数据。


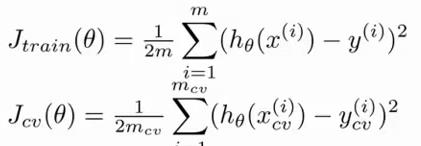
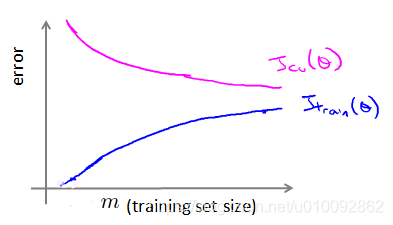
如何利用学习曲线识别高偏差/欠拟合： 作为例子，我们尝试用一条直线来适应下面的数据，可以看出，无论训练集有多么大误差都不会有太大改观：

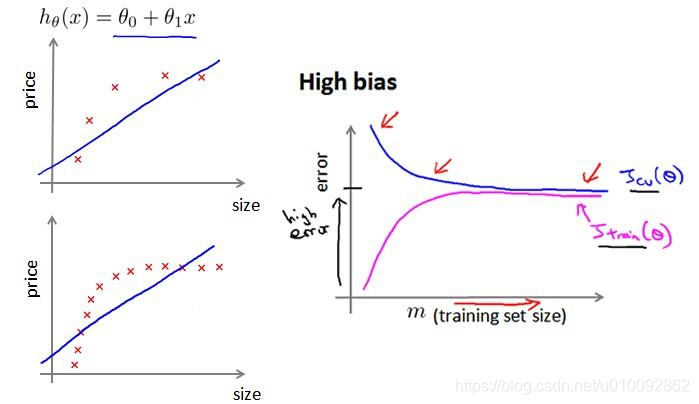
也就是说在高偏差/欠拟合的情况下，增加数据到训练集不一定能有帮助。如何利用学习曲线识别高方差/过拟合： 假设我们使用一个非常高次的多项式模型，并且归一化非常小，可以看出，当交叉验证集误差远大于训练集误差时，往训练集增加更多数据可以提高模型的效果。

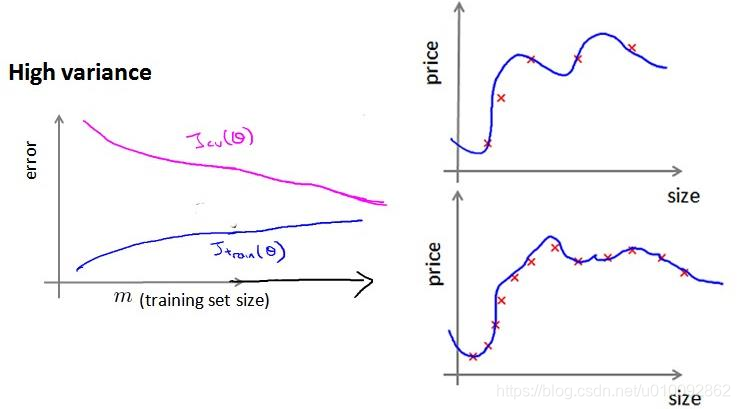
也就是说在高方差/过拟合的情况下，增加更多数据到训练集可能可以提高算法效果。

---

10.7 Deciding What to Do Next Revisited（蓦然回首）

怎样评价一个学习算法，我们讨论了模型选择问题，偏差和方差的问题。那么这些诊断法则怎样帮助我们判断，哪些方法可能有助于改进学习算法的效果，而哪些可能是徒劳的呢？
让我们再次回到最开始的例子，在那里寻找答案，这就是我们之前的例子。 回顾 1.1 中提出的六种可选的下一步，让我们来看一看我们在什么情况下应该怎样选择：

1. 获得更多的训练实例——解决高方差
2. 尝试减少特征的数量——解决高方差
3. 尝试获得更多的特征——解决高偏差
4. 尝试增加多项式特征——解决高偏差
5. 尝试减少归一化程度 λ——解决高偏差
6. 尝试增加归一化程度 λ——解决高方差
   神经网络的方差和偏差：
   
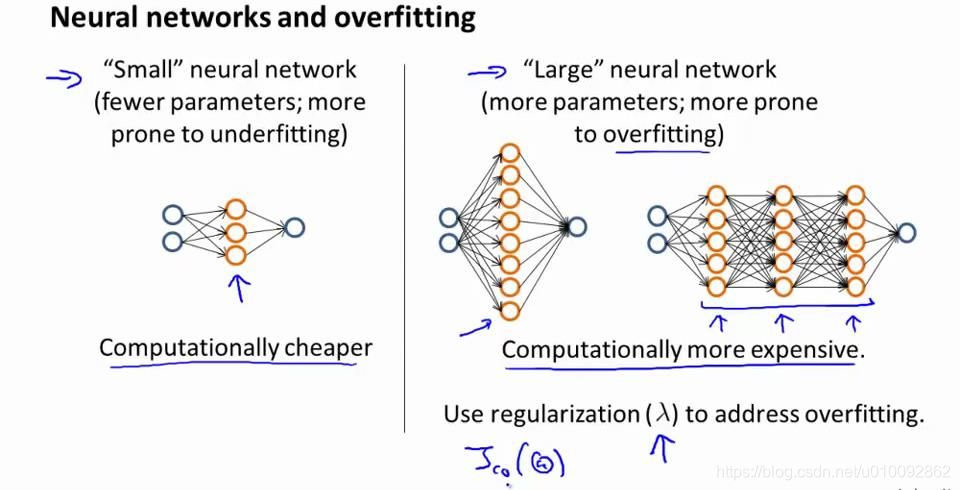
   使用较小的神经网络，类似于参数较少的情况，容易导致高偏差和欠拟合，但计算代价较小使用较大的神经网络，类似于参数较多的情况，容易导致高方差和过拟合，虽然计算代价比较大，但是可以通过正则化手段来调整而更加适应数据。
   通常选择较大的神经网络并采用正则化处理会比采用较小的神经网络效果要好。对于神经网络中的隐藏层的层数的选择，通常从一层开始逐渐增加层数，为了更好地作选择，可以把数据分为训练集、交叉验证集和测试集，针对不同隐藏层层数的神经网络训练神经网络， 然后选择交叉验证集代价最小的神经网络。

11 Machine Learning System Design

11.1 Prioritizing（优先化） What to Work On

首先要做的决定是如何选择并表达特征向量 x。我们可以选择一个由 100 个最常出现在垃圾邮件中的词所构成的列表，根据这些词是否有在邮件中出现，来获得我们的特征向量（出现为 1，不出现为 0），尺寸为 100×1。为了构建这个分类器算法，我们可以做很多事，例如：

1. 收集更多的数据，让我们有更多的垃圾邮件和非垃圾邮件的样本；
2. 基于邮件的路由信息开发一系列复杂的特征；
3. 基于邮件的正文信息开发一系列复杂的特征，包括考虑截词的处理；
4. 为探测刻意的拼写错误（把 watch 写成 w4tch）开发复杂的算法；

11.2 Error（误差） Analysis

误差分析（error analysis）的概念。最好的实践方法不是建立一个非常复杂的系统，拥有多么复杂的变量；而是构建一个简单的算法，这样你可以很快地实现它。
每当我研究机器学习的问题时，我最多只会花一天的时间，来试图很快的把结果搞出来，即便效果不好。即便运行得不完美，但是也把它运行一遍，最后通过交叉验证来检验数据。一旦做完，你可以画出学习曲线，通过画出学习曲线，以及检验误差，来找出你的算法是否有高偏差和高方差的问题，或者别的问题。在这样分析之后，再来决定用更多的数据训练，或者加入更多的特征变量是否有用。
这么做的原因是：你并不能提前知道你是否需要复杂的特征变量，或者你是否需要更多的数据，因为你缺少证据，缺少学习曲线。但是当你实践一个非常简单即便不完美的方法时，你可以通过画出学习曲线来做出进一步的选择。

你可以用这种方式来避免一种电脑编程里的过早优化问题，这种理念是：我们必须用证据来领导我们的决策，怎样分配自己的时间来优化算法，而不是仅仅凭直觉，凭直觉得出的东西一般总是错
误的。
除了画出学习曲线之外，一件非常有用的事是误差分析，当我们在构造垃圾邮件分类器时，我会看一看我的交叉验证数据集，然后亲自看一看哪些邮件被算法错误地分类。通过这些被算法错误分类的垃圾邮件与非垃圾邮件， 你可以发现某些系统性的规律： 什么类型的邮件总是被错误分类。 经常地这样做之后， 这个过程能启发构造新的特征变量， 或者告诉你： 现在这个系统的短处， 然后启发你如何去提高它。
构建一个学习算法的推荐方法为：

1. 从一个简单的能快速实现的算法开始，实现该算法并用交叉验证集数据测试这个算法；
2. 绘制学习曲线，决定是增加更多数据，或者添加更多特征，还是其他选择；
3. 进行误差分析：人工检查交叉验证集中我们算法中产生预测误差的实例，看看这些实例是否有某种系统化的趋势。

11.3 Error Metrics（度量） for Skewed（ 歪斜的） Classes

误差分析，以及设定误差度量值的重要性。那就是，设定某个实数来评估你的学习算法，并衡量它的表现，有了算法的评估和误差度量值。使用一个合适的误差度量值，这有时会对于你的学习算法造成非常微妙的影响，这件重要的事情就是偏斜类（skewed classes）的问题。 

类偏斜情况表现为我们的训练集中有非常多的同一种类的实例，只有很少或没有其他类的实例。例如我们希望用算法来预测癌症是否是恶性的，在我们的训练集中，只有 0.5%的实例是恶性肿瘤。假设我们编写一个非学习而来的算法，在所有情况下都预测肿瘤是良性的，那么误差只有 0.5%。然而我们通过训练而得到的神经网络算法却有 1%的误差。这时，误差的大小是不能视为评判算法效果的依据的。

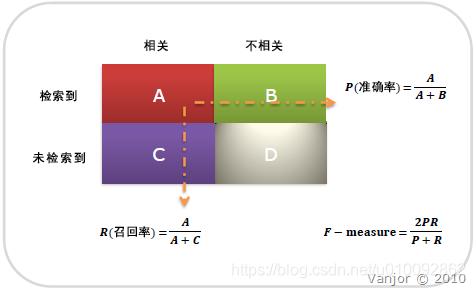
准确率（Precision），又称“精度”、“正确率”、“查准率”，表示在检索到的所有文档中，检索到的相关文档所占的比例。召回率（Recall），又称“查全率”，表示在所有相关文档中，检索到的相关文档所占的比率。

查准率（Precision）和查全率（Recall） 我们将算法预测的结果分成四种情况：

1. 正确肯定（True Positive,TP）：预测为真，实际为真；
2. 正确否定（True Negative,TN）：预测为假，实际为假；
3. 错误肯定（False Positive,FP）：预测为真，实际为假；
4. 错误否定（False Negative,FN）：预测为假，实际为真；
   则：
   查准率=TP/（TP+FP）例，在所有我们预测有恶性肿瘤的病人中，实际上有恶性肿瘤的病人的百分比，越高越好。
   查全率=TP/（TP+FN）例，在所有实际上有恶性肿瘤的病人中，成功预测有恶性肿瘤的病人的百分比，越高越好。
   这样，对于我们刚才那个总是预测病人肿瘤为良性的算法，其查全率是 0。

11.4 Trading Off Precision and Recall

查准率和召回率，作为遇到偏斜类问题的评估度量值，我们希望能够保证查准率和召回率的相对平衡。
假使，我们的算法输出的结果在 0-1 之间，我们使用阀值 0.5 来预测真和假。
查准率（Precision） =TP/（TP+FP） 例，在所有我们预测有恶性肿瘤的病人中，实际上有恶性肿瘤的病人的百分比，越高越好。
查全率（Recall） =TP/（TP+FN）例，在所有实际上有恶性肿瘤的病人中，成功预测有恶性肿瘤的病人的百分比，越高越好。
如果我们希望只在非常确信的情况下预测为真（肿瘤为恶性），即我们希望更高的查准率，我们可以使用比 0.5 更大的阀值，如 0.7， 0.9。这样做我们会减少错误预测病人为恶性肿瘤的情况，同时却会增加未能成功预测肿瘤为恶性的情况。
如果我们希望提高查全率，尽可能地让所有有可能是恶性肿瘤的病人都得到进一步地检查、诊断，我们可以使用比 0.5 更小的阀值，如 0.3。
我们可以将不同阀值情况下，查全率与查准率的关系绘制成图表，曲线的形状根据数据的不同而不同：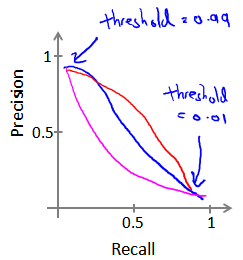
那么，在两者都要求高的情况下，如何综合衡量准确率和召回率呢？一般使用F值。 F-Measure是准确率（P）和召回率（R）的加权调和平均。公式为：

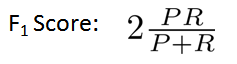
我们选择使得 F1 值最高的阀值。

11.5 Data For Machine Learning

在之前我们讨论了评价指标。这往往涉及到用来训练的数据有多少。在之前的一些视频中，我曾告诫大家不要盲目地开始，而是花大量的时间来收集大量的数据，因为数据有时是唯一能实际起到作用的。
得到大量的数据并在某种类型的学习算法中进行训练，可以是一种有效的方法来获得一个具有良好性能的学习算法。而这种情况往往出现在这些条件对于你的问题都成立并且你能够得到大量数据的情况下。这可以是一个很好的方式来获得非常高性能的学习算法。
什么时候我们会希望获得更多数据，而非修改算法。 他们所做的就是改变了训练数据集的大小，并尝试将这些学习算法用于不同大小的训练数据集中，这就是他们得到的结果.
假设特征值有足够的信息来预测 y值， 假设我们使用一种需要大量参数的学习算法， 比如有很多特征的逻辑回归或线性回归，或者用带有许多隐藏单元的神经网络， 那又是另外一种带有很多参数的学习算法， 这些都是非常强大的学习算法， 它们有很多参数， 这些参数可以拟合非常复杂的函数， 因此我要调用这些， 我将把这些算法想象成低偏差算法， 因为我们能够拟合非常复杂的函数， 而且因为我们有非常强大的学习算法， 这些学习算法能够拟合非常复杂的函数。 很有可能， 如果我们用这些数据运行这些算法， 这种算法能很好地拟合训练集， 因此， 训练误差就会很低了。现在假设我们使用了非常非常大的训练集， 在这种情况下， 尽管我们希望有很多参数，但是如果训练集比参数的数量还大， 甚至是更多， 那么这些算法就不太可能会过度拟合。 也就是说训练误差有希望接近测试误差。另一种考虑这个问题的角度是为了有一个高性能的学习算法， 我们希望它不要有高的偏差和方差。因此偏差问题， 我么将通过确保有一个具有很多参数的学习算法来解决， 以便我们能够得到一个较低偏差的算法， 并且通过用非常大的训练集来保证我们在此没有方差问题， 我们的算法将没有方差， 并且通过将这两个值放在一起， 我们最终可以得到一个低误差和低方差的学习算法。 这使得我们能够很好地测试测试数据集。 从根本上来说， 这是一个关键的假设：特征值有足够的信息量， 且我们有一类很好的函数， 这是为什么能保证低误差的关键所在。 它有大量的训练数据集， 这能保证得到更多的方差值，因此这给我们提出了一些可能的条件， 如果你有大量的数据， 而且你训练了一种带有很多参数的学习算法， 那么这将会是一个很好的方式， 来提供一个高性能的学习算法。
我觉得关键的测试： 首先， 一个人类专家看到了特征值 x， 能很有信心的预测出 y 值吗？因为这可以证明 y 可以根据特征值 x 被准确地预测出来。 其次， 我们实际上能得到一组庞大的训练集， 并且在这个训练集中训练一个有很多参数的学习算法吗？如果你不能做到这两者， 那么更多时候， 你会得到一个性能很好的学习算法。