如何判断任一内存地址是堆上的还是栈上，若是堆上的返回该内存长度

最新推荐文章于 2022-09-15 10:08:17 发布

原创最新推荐文章于 2022-09-15 10:08:17 发布 · 5.8k 阅读

7 ·

CC 4.0 BY-SA版权

内存分配专栏收录该内容

2 篇文章

订阅专栏

本文介绍了如何判断内存地址是否属于堆内存，以及如果是堆内存，如何计算其分配的长度。通过分析new操作的内存布局，利用_CrtMemBlockHeader结构体，查找内存块的头部和尾部标识来实现这一功能。文章还提到了栈和堆的生长方向，以及在Win64平台上的内存对齐和类大小计算。并提供了实例代码进行演示。

很早以前就想过这个问题：看到一个内存地址，如果判断这个地址是不是堆上的，若是，new出来的长度是多少字节？深入了解了new和delete的源码后，终于把这个方法找到了，在此分享给大家。

每个进程启动时候会有4G的虚拟内存，分为堆区、栈区、静态存储区、常量区、代码段、数据段和内核空间，而对每个线程，默认分配给其1MB空间。计算机一般采用的是小端模式存储，栈是向低地址生长，堆是向高地址生长。处于Ring3的应用程序是不可以访问内核空间（2G-64KB）的。

下面说一下new，新分配的内存前48字节为结构体_CrtMemBlockHeader（最后一个成员gap[4]=fdfdfdfd），后4字节为fdfdfdfd;这52字节时new的内存前后标示，若被破坏，则释放时会检查报错。于是可用下买呢方法来确定该地址是否在堆上，并计算出其长度：

//<<判断任一内存地址是否是堆内存，若是则返回内存长度，若不是返回-1

inline int CalcMemLen(void *pSrc, longfindRange = 10000)

{

//crt头文件不能包含，这里定义下

typedefstruct _CrtMemBlockHeader

{

struct_CrtMemBlockHeader * pBlockHeaderNext;

struct_CrtMemBlockHeader * pBlockHeaderPrev;

char* szFileName;

int nLine;

#if defined (_WIN64)|| defined (WIN64)

int nBlockUse;

size_t nDataSize;

#else /* _WIN64 */

size_t nDataSize;

int nBlockUse;

#endif /* _WIN64 */

long lRequest;

unsignedchar gap[4];

} _CrtMemBlockHeader;

#define pbData(pblock) ((unsignedchar *)((_CrtMemBlockHeader *)pblock + 1))

#define pHdr(pbData) (((_CrtMemBlockHeader *)pbData)-1)

#define _BLOCK_TYPE_IS_VALID(use) (_BLOCK_TYPE(use) ==_CLIENT_BLOCK || \

(use) == _NORMAL_BLOCK || \

_BLOCK_TYPE(use) == _CRT_BLOCK || \

(use) == _IGNORE_BLOCK)

static unsigned char_bNoMansLandFill = 0xFD;

unsignedchar *pc = (unsignedchar*)pSrc; //char*的话， -3不等于fd啊？

_CrtMemBlockHeader *pHead = NULL;

unsignedchar *pStart=NULL, *pEnd=NULL;

inti=0;

//找头部标示

for(i=0; i<findRange; i++)

{

if(pc[-i-4]==_bNoMansLandFill && pc[-i-3]==_bNoMansLandFill &&pc[-i-2]==_bNoMansLandFill && pc[-i-1]==_bNoMansLandFill)

{

pStart =&pc[-i];

pHead =pHdr(pStart);

break;

}

if(i>=findRange || !_BLOCK_TYPE_IS_VALID(pHead->nBlockUse))

{//指定范围内没有找到头部标示;或者找到了但不是有效的

return-1;

}

//找尾部标示

for(i=0; i<findRange; i++)

{

if(pc[i]==0xfd && pc[i+1]==0xfd && pc[i+2]==0xfd &&pc[i+3]==0xfd && pc[i+4] !=0xfd)//0xfd fd fdfd

{

pEnd = pc+i;

break;

}

if(i>=findRange)

{//指定范围内没有找到尾部标示;

return-1;

}

intlength = int(pEnd - pStart);

if(pHead->nDataSize == length)

{

if(_BLOCK_TYPE_IS_VALID(pHead->nBlockUse))

{

if (_CrtIsValidHeapPointer(pStart))

{

return pHead->nDataSize;

}

return-1;

}

下面在win64平台上测试一下：

class String

{

public:

/*explicit*/String(const char*str=NULL);//普通构造函数

String(constString &str);//拷贝构造函数

String & operator=(const String &str);//赋值函数

~String();//析构函数

private:

public:

char*m_data;//用于保存字符串

char m_c;

unsignedshort m_i;

};

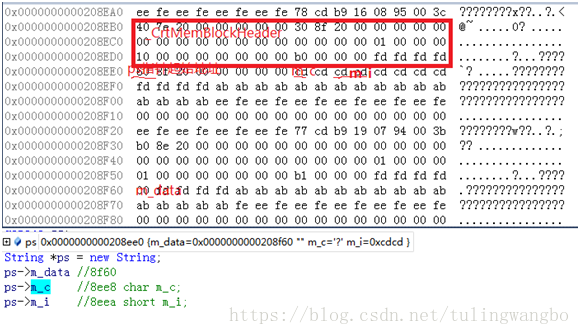
ps的地址为0x208ee0,起始0-7个字节存的是指针m_data的值，win64指针是8字节，小端模式倒过来就是0x0000000000208f60;第8个字节存储m_c;由于sizeof（usingned short）=2,故m_i要对齐到2的整数倍也就是10了，故第10-11字节8eea-8eeb存储m_i;最后整个类按照pragma pack指定的值8~~min{类内最长元素（m_data8字节），机器cpu长度（8字节）}~~对齐，那就是把12补齐到16了，故sizeof(String)==16；如果类前加一句#pragma pack(push,1)，则sizeof(String)==11；

由于构造函数中m_data=new char[1],故重新在堆上分配了内存，地址8f30-8f5f为其头部标示，8f61-8f64为其尾部标示。

测试结果：

int *aa = new int[10];
int allLen = CalcMemLen(aa);//40

int bb[1];
bb[2] = 9999;
allLen = CalcMemLen(bb);//-1

String *ps = new String;
allLen = CalcMemLen(ps);//16
allLen = CalcMemLen(&ps->m_i);//16
allLen = CalcMemLen(&ps->m_data);//16
allLen = CalcMemLen(ps->m_data);//1

char *pAppPath = NULL;
_get_pgmptr(&pAppPath);
allLen = CalcMemLen(pAppPath);//-1
delete pAppPath;//非堆内存，不可释放

2.变量一定要初始化，尤其是类和结构体的成员变量。一般地，对于win32上int变量i，在应用程序首次加载时：Debug模式下初始值为0xcccccccc，Release模式下初始值为0；但随着程序的运行，栈上的空间不断被该进程申请释放，下一次进入时，i可能是其他未预期的值。对于栈上的内存，无法计算其长度，数组越界访问了一般也不会报错（不过尽量保证不要越界，值得提醒一下，如果上面的bb定义在类String内，那么越界后就很容易破坏掉ps指针的边界，导致释放时报错）。