场景:正权有向边找最短路径
//自我讲解,可能不是你所想要的搜索回答。
举例:
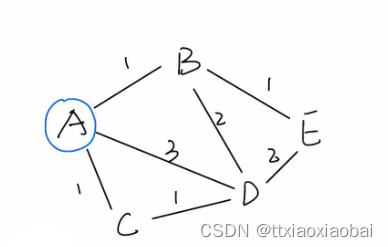
找到从A到E的最短路径
从A可到达B、C、D记录下来,(B 上一节点A,最短距离为1) ……
接着从记录的点中找到最短距离的那个点,这会有点B和C,然后更新(比如本来D点信息为上一个节点为A,最短距离为3,(由于当选节点C时,节点D要更新),更新为上一节点为C,最短距离为2)
注意要求权值为正值,是有必要的。
比如通过A可以找到B(1)、C(1)、D(3)的最短距离。
在更新E的最短距离时,假设DE之间距离为-4。
正常迪杰斯特拉算法要求 去求E点的最短路径,应该是按照E的上一个节点是B,E的最短距离为2.
但DE距离为负,本来死活不会 让E的上一个结点为D(也就是不会走经过D点这条路),按照这个负数距离,E的最短距离为1,最后最短距离为1.是不是很离谱?
//网络延迟时间,找到从K到所有结点的最短距离,使用迪杰斯特拉算法
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int n, int k) {
const int inf = INT_MAX / 2;
vector<vector<int> > g(n, vector<int>(n, inf)); //初始化结点之间无穷远
//memset(g, ox3f, sizeof(g));
for(auto &t : times){ //把数据保存在g[x][y] = 边长
int x = t[0] - 1 , y = t[1] - 1 ;
g[x][y] = t[2];
}
vector<bool> used(n, false);
vector<int> dist(n, inf);
//memset(dist, ox3f, sizeof(dist));
dist[k - 1] = 0; //起始点到起始点的距离为0
for(int i = 0; i < n; ++i){ //类似遍历矩阵行
int x = -1;
for(int j = 0; j < n;++j){ //找到 j点最短路径的上一个点x
if(!used[j] && (x == -1 || dist[j] < dist[x]) ){
x = j;
}
}
used[i] = true; //找到x后设置标记
for(int j = 0; j < n; ++j){ //
dist[j] = min(dist[j], g[x][j] +dist[x]); //求出y点的最短路径
}
}
int ans = *max_element(dist.begin(), dist.end()); //返回最大值
return ans == inf ? -1 : ans;
}
};








 文章探讨了在正权有向图中使用迪杰斯特拉算法寻找从特定节点到其他所有节点的最短路径的问题,强调了当存在负权重时算法的局限性,并提供了一个C++实现来计算网络延迟时间。
文章探讨了在正权有向图中使用迪杰斯特拉算法寻找从特定节点到其他所有节点的最短路径的问题,强调了当存在负权重时算法的局限性,并提供了一个C++实现来计算网络延迟时间。
















 2350
2350

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








