迁移学习基础知识——其他度量准则（KL散度与JS距离、MMD、PA、A-distance、HSIC）-优快云博客

Hi，大家好，我是半亩花海。在上节说明了迁移学习领域的总体思路和度量准则（距离和相似度）之后，本文主要将介绍迁移学习的其他度量准则（这里主要说明的是几种分布距离度量方法，诸如KL散度与JS距离、MMD、PA、A-distance、HSIC）。首先讲解了KL散度（非对称相对熵）和JS距离（对称化改进），然后重点分析了最大均值差异（MMD）及其多核扩展MK-MMD，该方法通过核映射在高维空间计算分布差异。此外还介绍了PA方法（计算格拉斯曼流形上的主角度）、A-distance（基于分类器损失的领域差异度量）以及HSIC（希尔伯特空间独立性检验）。

三、Principal angle (PA)

四、A-distance

五、Hilbert-Schmidt Independence Criterion (HSIC)

六、参考资料

一、KL散度与JS距离

KL 散度和 JS 距离是迁移学习中被广泛应用的度量手段。

（1）KL散度

Kullback–Leibler divergence，又叫做相对熵，衡量两个概率分布 $P(x), Q(x)$ 的距离：

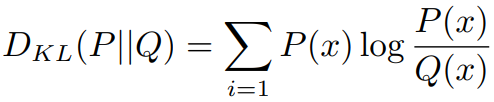
这是一个非对称距离：。

（2）JS距离

Jensen–Shannon divergence，基于 KL 散度发展而来，是对称度量：

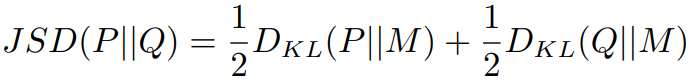
其中。

二、最大均值差异 (MMD)

最大均值差异是迁移学习中使用频率最高的度量。Maximum mean discrepancy，它度量在再生希尔伯特空间中两个分布的距离，是一种核学习方法。两个随机变量的距离为：

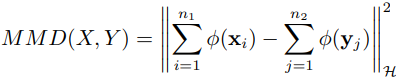
其中 ϕ(·) 是映射，用于把原变量映射到再生核希尔伯特空间 (Reproducing Kernel Hilbert Space, RKHS) 中。什么是 RKHS？形式化定义太复杂，简单来说就是这个空间是对于函数的内积完备的。就是比欧几里得空间更高端的。

理解：就是求两堆数据在 RKHS 中的均值的距离。

多核的 MMD：Multiple-kernel MMD，简称 MK-MMD。现有的 MMD 方法是基于单一核变换的，多核的 MMD 假设最优的核可以由多个核线性组合得，而MK-MMD 在许多后来的方法中被大量使用。

三、Principal angle (PA)

也是将两个分布映射到高维空间 (格拉斯曼流形) 中，在流形中两堆数据就可以看成两个点。Principal angle 是求这两堆数据的对应维度的夹角之和。

对于两个矩阵 $\mathbf{X},\mathbf{Y}$ ，计算方法：首先正交化 (用 PCA) 两个矩阵，然后：

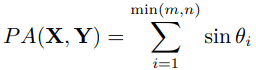
其中 $m, n$ 分别是两个矩阵的维度， $\theta_{i}$ 是两个矩阵第 $i$ 个维度的夹角， $\Theta = {\theta_{1}, \theta_{2}, \cdot \cdot \cdot, \theta_{t}}$ 是两个矩阵 SVD 后的角度：

四、A-distance

A-distance 是一个很简单却很有用的度量。2007年的一篇经典文献中介绍了此距离，它可以用来估计不同分布之间的差异性。A-distance 被定义为建立一个线性分类器来区分两个数据领域的 hinge 损失 (也就是进行二类分类的 hinge 损失)。它的计算方式是，我们首先在源域和目标域上训练一个二分类器 $h$ ，使得这个分类器可以区分样本是来自于哪一个领域。我们用 $err(h)$ 来表示分类器的损失，则 A-distance 定义为：