poj1753 (翻硬币游戏）

Description

Flip game is played on a rectangular 4x4 field with two-sided pieces placed on each of its 16 squares. One side of each piece is white and the other one is black and each piece is lying either it's black or white side up. Each round you flip 3 to 5 pieces, thus changing the color of their upper side from black to white and vice versa. The pieces to be flipped are chosen every round according to the following rules:
Choose any one of the 16 pieces.
Flip the chosen piece and also all adjacent pieces to the left, to the right, to the top, and to the bottom of the chosen piece (if there are any).
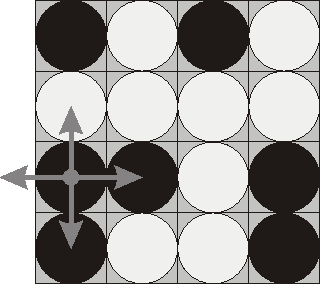Consider the following position as an example:
bwbw
wwww
bbwb
bwwb
Here "b" denotes pieces lying their black side up and "w" denotes pieces lying their white side up. If we choose to flip the 1st piece from the 3rd row (this choice is shown at the picture), then the field will become:
bwbw
bwww
wwwb
wwwb
The goal of the game is to flip either all pieces white side up or all pieces black side up. You are to write a program that will search for the minimum number of rounds needed to achieve this goal.

Input

The input consists of 4 lines with 4 characters "w" or "b" each that denote game field position.

Output

Write to the output file a single integer number - the minimum number of rounds needed to achieve the goal of the game from the given position. If the goal is initially achieved, then write 0. If it's impossible to achieve the goal, then write the word "Impossible" (without quotes).

Sample Input

bwwb

bbwb

bwwb  

bwww

Sample Output

4  

思路：枚举+组合。n轮有C(16,n)种方法，枚举所有方法，找到最小的轮数

#include<iostream>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<algorithm>
#include<functional>
#include<iomanip>

//using namespace std;
int min=3000;
void combine(int a[], int n, int m,  int b[], const int M )
{
  for(int i=n; i>=m; i--)   // 注意这里的循环范围
  {
    b[m-1] = i - 1;

    if (m>1)
      combine(a,i-1,m-1,b,M);

    else                     // m == 1, 输出一个组合
    {
      for(int j=M-1; j>=0; j--)
      {
         a[b[j]]=1-a[b[j]];     
         int x=b[j]%4;
         int y=b[j]/4;
         if (x>0)
             a[y*4+x-1]=1-a[y*4+x-1];
         if (x<3)
             a[y*4+x+1]=1-a[y*4+x+1];
         if (y>0)
             a[(y-1)*4+x]=1-a[(y-1)*4+x];
         if (y<3)
             a[(y+1)*4+x]=1-a[(y+1)*4+x];
      }
      int test=0;
      for (int k=0;k<16;k++)   
          test+=a[k];
      if (test==0||test==16){             
         min=(min<M?min:M); 
      }
     
      for(int j=M-1; j>=0; j--)
      {
         a[b[j]]=1-a[b[j]];     
         int x=b[j]%4;
         int y=b[j]/4;
         if (x>0)
             a[y*4+x-1]=1-a[y*4+x-1];
         if (x<3)
             a[y*4+x+1]=1-a[y*4+x+1];
         if (y>0)
             a[(y-1)*4+x]=1-a[(y-1)*4+x];
         if (y<3)
             a[(y+1)*4+x]=1-a[(y+1)*4+x];
      }
      
    }
  }
}

int main()
{
   char input[16];
   
   for (int i=0;i<4;i++)
   {
       char row[5];
       std::cin>>row;
       input[i*4]=row[0];
       input[i*4+1]=row[1];
       input[i*4+2]=row[2];
       input[i*4+3]=row[3];
   }
       
 //       cin>>input[i*4]>>input[i*4+1]>>input[i*4+2]>>input[i*4+3]>>endl;
   int test=0;     
   int temp[16];
   for (int j=0;j<16;j++)
       {     
           if (input[j]=='b')
               temp[j]=0;
           else
               temp[j]=1;
        //   std::cout<<temp[j];
       }
    for (int k=0;k<16;k++)
          test+=temp[k];
      if (test==0||test==16)
      {
         std::cout<<0;
    //     system("pause");
         return 0;
         }
       
   for (int i=0;i<16;i++)
   {
       int *b =new int[i+1];
       combine(temp,16,i+1,b,i+1);           
   } 
   if (min==3000)
        std::cout<<"Impossible";
        else
           std::cout<<min;
   
  //  system("pause");
  return 0;
}