这里写自定义目录标题
监督学习和非监督学习
监督学习就是给你一本作业本,后面有答案,自己先做,做完之后对答案,对了ok,不对调整自己的答案,让自己的答案尽最大可能是正确答案。
非监督学习就是给你一本作业本,没答案,自己做。
监督学习中,有一个label,让计算机根据这个label学习;非监督学习中没有。
监督学习主要研究的问题:回归和分类
非监督学习主要研究的问题:聚类
神经网络就是基于监督学习的。
前向传播
对于一个还没有训练好的神经网络而言,各个神经元之间的参数都是随机值,即初始化时赋的值,前向传播过程是神经网络的输入输出过程,即网络是如何根据X的值得到输出的Y值的。
设激活函数为f,权重矩阵为W,偏置项为b,输入为A,输出为Y,则Y = f(AW+b),计算Y这个过程就是前向传播的过程。
注意:权重矩阵W一开始是个随机值
在样本中我们的数据是(x,label),而y是我们经过神经网络计算出来的值,也就是估计值,y和label肯定有误差,如何减少误差,需要改变权重矩阵W,反向传播就是解决这个问题的。
反向传播和梯度下降
反向传播是为了减小误差,使得误差最小的权重矩阵的值便是神经网络最终的权重矩阵。对于误差的描述可以采用代价(误差)函数来描述,比如高中学的: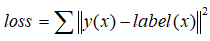 ,其中y(x)是神经网络的预测值,label(x)是x对应的真实值,可以看出loss是关于权重矩阵的多元函数,当loss最小时W的取值,便是神经网络权重矩阵最终值。
,其中y(x)是神经网络的预测值,label(x)是x对应的真实值,可以看出loss是关于权重矩阵的多元函数,当loss最小时W的取值,便是神经网络权重矩阵最终值。
反向传播的核心算法是梯度下降算法,既然反向传播是为了使loss最小,使得loss收敛的最快。根据场论的知识,梯度的方向是函数值增长最快的方向,那么梯度的反方向便是函数值减少最快的方向。基于这一理论,便有了梯度下降法。
梯度下降法的基本思想可以类比为一个下山的过程。假设这样一个场景:一个人被困在山上,需要从山上下来(找到山的最低点,也就是山谷)。但此时山上的浓雾很大,导致可视度很低。因此,下山的路径就无法确定,他必须利用自己周围的信息去找到下山的路径。这个时候,他就可以利用梯度下降算法来帮助自己下山。具体来说就是,以他当前的所处的位置为基准,寻找这个位置最陡峭的地方,然后朝着山的高度下降的地方走,同理,如果我们的目标是上山,也就是爬到山顶,那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离,都反复采用同一个方法,最后就能成功的抵达山谷。如图所示:

可以看到,梯度下降是一个循环或递归的过程,每走一段距离都要执行相同的算法,每次走的距离在梯度下降法称之为学习率(learning rate),如果学习率过大,那么可能会错过最低点;相反,如果学习率过小,那么到达最低点的时间会很长,即函数收敛时间较慢。梯度下降算法的核心公式如下:
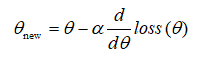

























 1408
1408

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








