问题描述
小凯手中有两种面值的金币,两种面值均为正整数且彼此互素。每种金币小凯都有无数个。在不找零的情况下,仅凭这两种金币,有些物品他是无法准确支付的。
现在小凯想知道:
-
在无法准确支付的物品中,最贵的价值是多少金币?
-
共有多少种无法支付的物品?
注意:输入数据保证存在小凯无法准确支付的商品。
解法
(1)假设两种钱每种最少要拿一次(也就是不能不拿),不能凑成的最小钱数为k,因为a和b互质,显然,k = a * b,(当k = a * b 时,由于ab互质,要么a拿b个,要么b拿a个)。
由于a和b可以一样都不拿,所以ans =k-a-b=a*b-a-b
(2)因为ab互质,所以a,b其中一个肯定是奇数。
设共有ans2个数不能购买
<1>a,b其中一个为偶数
推出ans2=((a-1)*(b-2)+(a-1))/2或((a-2)*(b-1)+(b-1))/2
化简得:ans2=(a-1)*(b-1)/2
<2>a,b全为奇数
推出ans2=(a-1)*(b-1)/2
综上ans=(a-1)*(b-1)/2下面是枚举的几个例子(方便理解):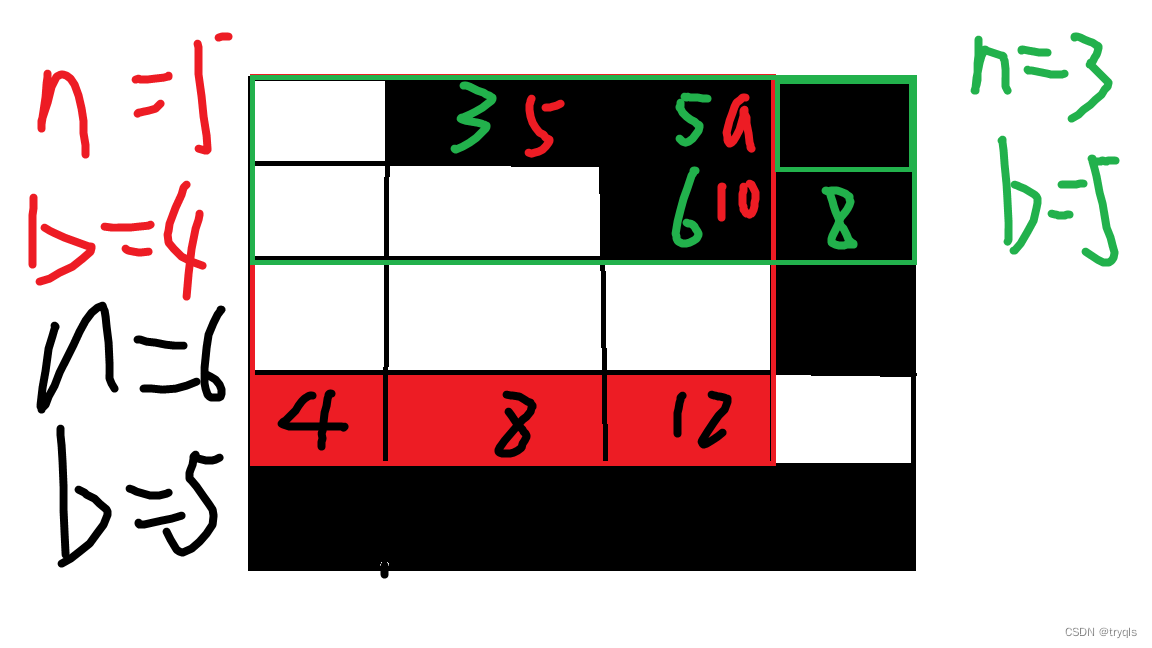




 文章描述了一个数学问题,小凯有互素面值的金币,无法支付某些商品。最小无法支付金额是两面值乘积减去两者之和。无法支付的商品数量是(a-1)*(b-1)/2,其中a和b是金币面值。此问题涉及到数论和算法。
文章描述了一个数学问题,小凯有互素面值的金币,无法支付某些商品。最小无法支付金额是两面值乘积减去两者之和。无法支付的商品数量是(a-1)*(b-1)/2,其中a和b是金币面值。此问题涉及到数论和算法。
















 1486
1486










