PTA 最大子列和问题 四种方法

例如给定序列{ -2, 11, -4, 13, -5, -2 }，其连续子列{ 11, -4, 13 }有最大的和20。现要求你编写程序，计算给定整数序列的最大子列和。

一.三层循环 O(n ^ n ^ n) 时间复杂度过高

//法一:三层循环 O(n^n^n)
int MaxSum(int a[], int n)
{
	int i, j, k;
	int thisSum, maxSum = 0;
	for(i = 0; i < n; i++){
		for(j = i; j < n; j++){
			thisSum = 0;
			for(k = i; k <= j; k++){
				thisSum += a[k];
				if(thisSum > maxSum){
					maxSum = thisSum;
				}
			}
		}
	}
	return maxSum;
}

二.两层循环 O(n ^ n)
在原来的基础上进行优化

//法二：两层循环 O(n^n) 
int MaxSum(int a[], int n)
{
	int i, j;
	int thisSum, maxSum = 0;
	for(i = 0 ; i < n; i++){
		thisSum = 0; 
		for(j = i ; j < n; j++){
			thisSum += a[j];
			if(thisSum > maxSum){
				maxSum = thisSum;
			}
		}
	}
	return maxSum;
} 

三.分治算法 O(nlogn)
1.原理
对于一个规模为n的问题，若该问题可以容易地解，比如说规模n较小）则直接解决，否则将其分解为k个规模较小的子问题，这些子问题互相独立且与原问题形式相同，递归地解这些子问题，然后将各子问题的解合并得到原问题的解。
分----将原问题分解为规模更小的子问题
治----将这些规模更小的子问题逐个击破
合----将已解决的子问题合并，最终得出原问题的解
2.方法
①将序列从中分为左右两个子序列
②递归求得两个子列的最大和
③从中分点分头向左、右两边扫描，找出跨过分界线的最大子列和
④输出这三个子列和最大的一个

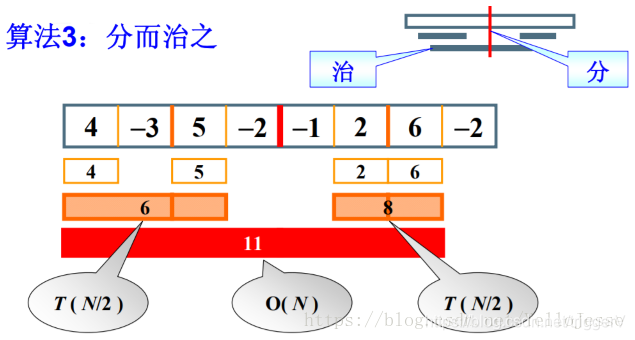
3.代码

//法三：分治算法 O(nlogn) 
int Max3 ( int A, int B, int C ) /*返回三个整数的最大值*/
{
	return (A > B) ? (A > C ? A : C) : (B > C ? B : C);
}
/*分治法求a[left]到a[right]的最大子列和*/
int DivideAndConquer ( int List[], int left, int right )
{
	int MaxLeftSum, MaxRightSum;    //存放左右子问题的解
	int MaxLeftBorderSum, MaxRightBorderSum;    //存放跨分界线的结果
	int LeftBorderSum, RightBorderSum;
	int center, i;
    /*递归的终止条件，子列只有1个数字*/
	if ( left == right ) {
		if ( a[left] > 0 ){
			return a[left];
		}else{
			return 0;
		}	
	}
    /* “分”的过程 */
	center = ( left + right ) / 2;    //找到中分点。
	MaxLeftSum = DivideAndConquer ( a, left, center );        //递归求左子列和
	MaxRightSum = DivideAndConquer ( a, center + 1, right );    //递归求右子列和
	
    /*求跨分界线的最大子列和*/
	MaxLeftBorderSum = 0;	LeftBorderSum = 0;
	for ( i = center; i >= left; i-- ) {
		LeftBorderSum += a[i];
		if ( LeftBorderSum > MaxLeftBorderSum ){
			MaxLeftBorderSum = LeftBorderSum;
		}
	}//左边扫描结束
	
	MaxRightBorderSum = 0;	RightBorderSum = 0;
	for ( i = center + 1; i <= right; i++ ) {
		RightBorderSum += a[i];
		if ( RightBorderSum > MaxRightBorderSum ){
			MaxRightBorderSum = RightBorderSum;
		}
	}//右边扫描结束
    /*返回“治”的结果*/
	return Max3 ( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
}
/*此函数用于保持接口相同*/
int MaxSum(int a[], int n)
{
	return DivideAndConquer (a, 0, n-1 );
}

四.在线处理 O(n)

//法四：在线处理 O(n)
int MaxSum(int a[], int n)
{
	int i;
	int thisSum = 0, maxSum = 0;
	for(i = 0 ; i < n; i++){
		thisSum += a[i];
		if(thisSum > maxSum){
			maxSum = thisSum;
		}
		if(thisSum < 0){     //任何负的子序列都不可能是最大子序列的前缀
			thisSum = 0;
		}
	}
	return maxSum;
}