01_sklearn--监督学习——广义线性模型，普通最小二乘法

1.1.广义线性模型

本章节主要讲述一些用于回归的方法，其中目标值y是输入变量x的线性组合。数学概念表示为：如果是预测值，那么有：

        (w,x)= + +...+

在整个模块中，我们定义向量作为coef_,定义作为intercept_。

如果需要使用广义线性模型进行分类，请参阅logistic回归。

1.1.1.普通最小二乘法

LinearRegression拟合一个带有系数的线性模型，使得数据集实际观测数据和预测数据（估计值）之间的残差平方和最小。其数学表达式为：

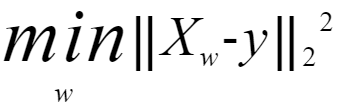
LinearRegression会调用fit方法来拟合数组X,y,并且将线性模拟的系数w存储在其成员变量coef_中：

# -*- coding: UTF-8 -*-

from sklearn import linear_model

reg = linear_model.LinearRegression()

print(reg.fit([[0,0],[1,1],[2,2]],[0,1,2]))
print(reg.coef_)

输出结果：

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)
[0.5 0.5]

然而，对于普通最小二乘的系数估计问题，其依赖于模型各项的相互独立性。当各项是相关的，且设计矩阵 X 的各列近似线性相关，那么，设计矩阵会趋向于奇异矩阵，这种特性导致最小二乘估计对于随机误差非常敏感，可能产生很大的方差。例如，在没有实验设计的情况下收集到的数据，这种多重共线性（multicollinearity）的情况可能真的会出现。

示例：线性回归示例（https://scikit-learn.org/stable/auto_examples/linear_model/plot_ols.html）

 

1.1.1.1.普通最小二乘法的复杂度

{% end raw %}

该方法使用 X 的奇异值分解来计算最小二乘解。如果 X 是一个形状为 (n_samples, n_features)的矩阵，设 {% math %} n{samples} \geq n{features} {% endmath %} , 则该方法的复杂度为 {% math %} O(n{samples} n{fearures}^2) {% endmath %}

{% raw %}

1.1.2 岭回归

Ride回归通过对系数的大小施加惩罚来解决 "普通最小二乘法"的一些问题。岭系数最小化的是带罚项的残差平方和。

其中，a >= 0是控制系数收缩量的复杂性参数：a的值越大，收缩量越大，模型对共线性的鲁棒性也更强。

与其它线性模型一样，Ride用fit方法完成拟合，并将模型系数w存储在其coef_成员中：

from sklearn import linear_model

reg = linear_model.Ridge (alpha = .5)
print(reg.fit ([[0, 0], [0, 0], [1, 1]], [0, .1, 1]))
print("--------------------------------------")
print(reg.coef_)
print("--------------------------------------")
print(reg.intercept_)

输出结果：

Ridge(alpha=0.5, copy_X=True, fit_intercept=True, max_iter=None,
      normalize=False, random_state=None, solver='auto', tol=0.001)
--------------------------------------
[0.34545455 0.34545455]
--------------------------------------
0.1363636363636364