sklearn代码实例学习笔记-1.1.1普通最小二乘法

1.算法

线性回归会拟合一个带有系数的模型，使得数据集实际观测数据和预测数据（估计值）之间的残差平方和最小。其数学表达式为:

2.线性回归实例（Linear Regression Example）

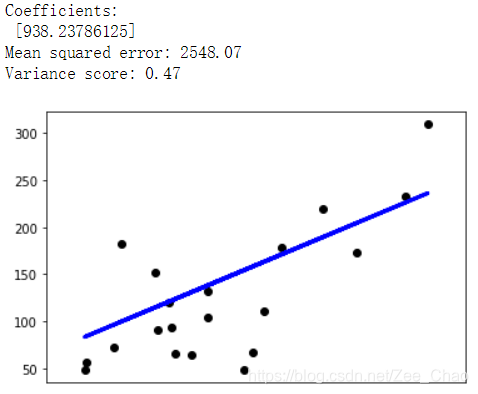
此实例仅使用“糖尿病”数据集的第一个特征（实际上是其中一个），以展现回归技术的二维图。 从图中直线可以发现，显示线性回归是如何尝试绘制直线的。该直线将尽可能地最小化数据集中观察到的结果之间的残差平方和线性近似预测的结果。

另外，该实例还计算了系数矩阵，残差平方和还有方差分数（拟合程度R^2）。

This example uses the only the first feature of the diabetes dataset, in order to illustrate a two-dimensional plot of this regression technique. The straight line can be seen in the plot, showing how linear regression attempts to draw a straight line that will best minimize the residual sum of squares between the observed responses in the dataset, and the responses predicted by the linear approximation.

The coefficients, the residual sum of squares and the variance score are also calculated.

# Code source: Jaques Grobler
# License: BSD 3 clause

import matplotlib.pyplot as plt
import numpy as np
# 对应包的描述分别见：
# https://scikit-learn.org/stable/modules/classes.html#module-sklearn.datasets
# https://scikit-learn.org/stable/modules/classes.html#module-sklearn.linear_model
# https://scikit-learn.org/stable/modules/classes.html#sklearn-metrics-metrics
from sklearn import datasets, linear_model
# 导入“均方差指标”和“R^2指标”
from sklearn.metrics import mean_squared_error, r2_score

# 加载糖尿病数据集
# Load the diabetes dataset
# 语句解释见：
# https://scikit-learn.org/stable/modules/generated/sklearn.datasets.load_diabetes.html#sklearn.datasets.load_diabetes
diabetes = datasets.load_diabetes()

# 只使用其中的一个特征进行回归分析（这里采用的是原数组中的第2列数据，将其提取出来并设置为列向量）
# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]

# 将数据的特征分割成训练集和测试集
# Split the data into training/testing sets
# 前422个数据作为训练集，后20个作为测试集
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]

# 对标签也做同样的分割
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]

# 创建线性回归模型的对象
# Create linear regression object
# 语句解释见：
# https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression
regr = linear_model.LinearRegression()

# 用训练集训练数据
# Train the model using the training sets
# 语句解释见：
# https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression.fit
regr.fit(diabetes_X_train, diabetes_y_train)

# 用测试集测试数据
# Make predictions using the testing set
# 语句解释见：
# https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LinearRegression.html#sklearn.linear_model.LinearRegression.predict
diabetes_y_pred = regr.predict(diabetes_X_test)

# 打印系数矩阵
# The coefficients
print('Coefficients: \n', regr.coef_)

# 打印均方差
# The mean squared error
# 语句解释见：
# https://scikit-learn.org/stable/modules/generated/sklearn.metrics.mean_squared_error.html#sklearn.metrics.mean_squared_error
print("Mean squared error: %.2f"
      % mean_squared_error(diabetes_y_test, diabetes_y_pred))

# 打印R^2值，这个值越接近1，说明拟合的效果越好
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))

# 结果可视化
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test,  color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)

# 横坐标轴不标记任何刻度，纵坐标轴使用默认刻度
plt.xticks(())
plt.yticks()

plt.show()

运行结果：

3.复杂度

该方法使用 X 的奇异值分解来计算最小二乘解。如果 X 是一个 size 为 (n, p) 的矩阵，若n大于等于p，则该算法复杂度为O(np^2)。