具有提供者约束的多涉众推荐Multis takeholder Recommendation with Provider Constraints

摘要：

推荐系统的设计通常是为了优化最终用户的效用。然而，在许多设置中，最终用户并不是唯一的涉众，这种排他性的关注可能会给其他涉众带来不满意的结果。在将买家和卖家聚集在一起的多面平台上就可以找到这样的场景。在这样的平台上，可能有必要共同优化买卖双方的价值。提出了一种基于约束的整数规划优化模型，利用不同的约束集来反映不同利益相关者的目标。该模型作为一个后处理步骤应用，因此可以很容易地将其添加到现有的推荐系统中，使其能够被多个涉众所感知。对于较大数据集的计算可处理性，利用拉格朗日对偶和子梯度优化方法对整数问题进行了重新构造。在两个数据集的实验中，我们对买卖双方效用之间的相互作用进行了实证评估，结果表明，我们的近似在实际情况下可以达到较好的上界和下界。

下面纯属个人理解，欢迎指错：

主要解决的问题：A multisided platform(MSP)是一种商业问题，它可以帮助交易中的各方找到彼此，并进行业务往来，从而降低交易成本。像•Buyers / sellers买卖方: Amazon Marketplace, JD.com, Etsy, eBay,Tienmao, Taobao, Rakuten, ShopRunner.
                  • Viewers / venues / events观众/场地/活动: Fandango, Ticketmaster.
                  • Riders / drivers乘客司机: Uber, Lyft.
                  • Hosts / guests租房: AirBnB, VRBO
                  • Users / advertisers / content developers用户/广告商/内容开发者: Facebook, Tumblr,and other social media applications.

           传统的推荐系统和推荐算法不能很好满足MPS系统内 的推荐任务，MPS内使用的推荐系统，除了关注最终用户外，还要考虑平台内各方（主要是提供者和购买者）的利益。本文所描述的方法将MSP设置中的多涉众推荐问题作为一个后处理优化步骤，不依赖于任何特定的算法方法来生成推荐，可以得到广泛的应用。

解决思路：利用约束的最优化问题。我们想要为每个消费者确定也满足某些提供者约束的top-k项。这需要解决一个大型整数规划问题，这个问题在计算上太复杂，所以作者通过对原优化问题提出拉格朗日松弛，然后用次梯度法求解。

提出的模型：这类问题其实属于多目标问题（同时考虑需求方和服务方的利益），解决多目标问题的一个方法是通过联合不同目标作为对你目标优化问题，并提出多目标的约束优化框架。

•     M1模型：对零售商所在的推荐列表上的总效用进行设置约束（即，限制每个类目下，每个零售商的item的数量），利用贪婪方法，给每个用户推荐K个item，其中可能移除某个活跃商过多的item，如移除后达不到K个，则随机挑选零售商的item进行推荐，直到K个。                                                                                                          ======>每个零售商的最小曝光度
•     M2模型：比M1增加了一个约束，即每个推荐列表中应该包含的最少数量的零售商。识别出不满足零售商多样性的用户，并移走频繁的零售商，加入不在列表内的零售商的item                                                   ======>确保零售商的多样性

下面解释的2个概念：

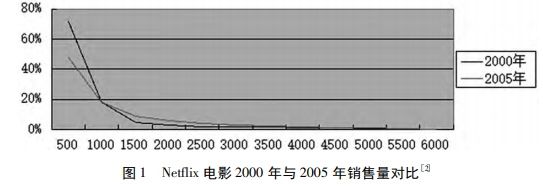
• 长尾分布：在安德森的书中提到了 Netflix 电影销售量的例子，从下图中可以看 出，Netflix 在 2000 年时销售量很高的 Top500 部电影在 2005 年时需求量 有了大幅降低，而在 2000 年时销量一般、大部分都不足 5% 的电影在 2005 年时需求量增大，更令人惊奇的是，当年 15% 的需求都来源于排 序位于 3000 之后的电影。

 

• 格朗日松弛：属于确定下界的算法，适用整数规划问题中，决策变量为较大整数时。基本原理：将目标函数中造成问题难的约束吸收到目标函数中，并保持目标函数的线性，使问题容易求解。

                具体求解步骤（次梯度法）：

            LR方法的可以表述为如下形式

                 

                 先对x求极小，然后x就没有了也就是变成了仅仅关于  的函数  ，然后再对  求极大值。也就是我们在一些书上可能会看到了极小极大化问题，根本的来源是LR方法。

             那么如何求解这个问题呢，我们这里简要介绍一下LR的求解框架，

             1 一般先随机给一个初始的 

            2 把  代入到  中，然后求解松弛问题也就是  ，解完得到一个当前步的最优的  。

            3 然后将这个  代入到  ，然后求解对偶问题  ，得到 

            4令  ，判断是否停止，若没停止跳到第2步继续执行。

            由于要先极大再极小，我们只能先固定住一个变量，在求解另一个变量，然后反复的迭代。整个算法流程就是先固定  ，对  求极小，然后固定住  ，对  求极大，然后反复进行。LR相关的论文可以证明该算法的收敛性。

Discussion

未来在这方面的研究有很多机会。需要进一步的研究来改进一些比较复杂的情况下的界限。我们还计划用更大的数据集进行实验，并仔细研究近似的计算权衡。该方法决定了在多大程度上偏向于一个零售商而不是另一个，但如何设置这些值仍然存在一些悬而未决的问题。αr值应如何设置的长期利润最大化?除了MSPs，在其他涉及多个利益相关者的情况都是有用的。我们还对MSP的内部动态可以作为我们模型的零售商促销方面的输入的条件感兴趣。我们可以将MSP中的提供者看作一个网络，其中节点之间的连接强度由相互交叉销售的客户数量决定。作为进一步的研究，供应商网络结构可以集成到我们的数学模型中。