sklearn-回归算法-线性回归

算法思想： 根据历史数据，找到最佳的一组权重 w，和偏置b，根据?_1 ?_1+?_2 ?_2+…+?_? ?_?+? 求出目标值，在计算loss损失，在梯度下降 ，调整w权重。

该算法针对于 连续型，非离散型数据

二元线性回归:（样本就2个特征）

目标值 = 权重1 * 特征值1 + 权重2 * 特征值2 +b

n元线性回归（样本选择n个特征）

目标值 = 权重1 * 特征值1 + 权重2 * 特征值2 +·········+ 权重n * 特征值n+b

公式

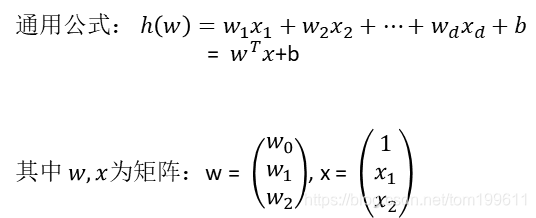
运算。

X = [[1，2，3], [4，5，6], [7，8，9]， [6，6，1]]


行=样本数，列= 选取的特征数量


最终结果的形状是 二维 [4,1] 有4个样本，每个样本一个输出

w的形状 二维的[3,1]


w = [[w1],[w2],[w3]] 和特征数量一致

b = [[b1],[b2],[b3],[b4]] 每个样本都有一个偏置量

结果 = np.matmul(x,w) + b

loss损失函数？？

使用