sklearn -分类算法 -决策树

最新推荐文章于 2022-01-10 17:48:59 发布

原创

最新推荐文章于 2022-01-10 17:48:59 发布 · 置顶 · 293 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#决策树

本文介绍了决策树的基础知识，包括信息熵和信息增益的概念。信息熵用于衡量数据的不确定性，而信息增益则用于确定最优特征划分。通过计算信息增益，可以构建决策树，将不确定性下降最大的特征放在树的前面。 sklearn库中的决策树API提供了如criterion（默认为'gini'，可选'entropy'）和max_depth等参数来控制决策树的构建。

`信息熵`（香农提出）

在这里插入图片描述
= 每一种类别的概率 * log 概率，求和，再乘以 -1

信息熵衡量不确定性，信息熵越小，不确定性也越小。信息熵越大，不确定性越大。

`信息增益` ：

表示得知特征A的信息之后，信息熵减少的程度。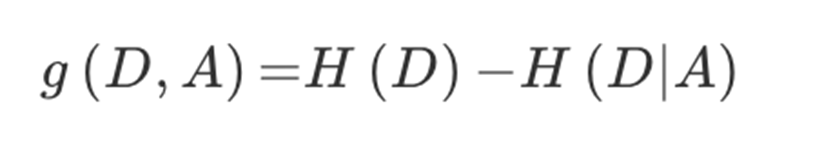在这里插入图片描述
= 初始信息熵 – A条件信息熵

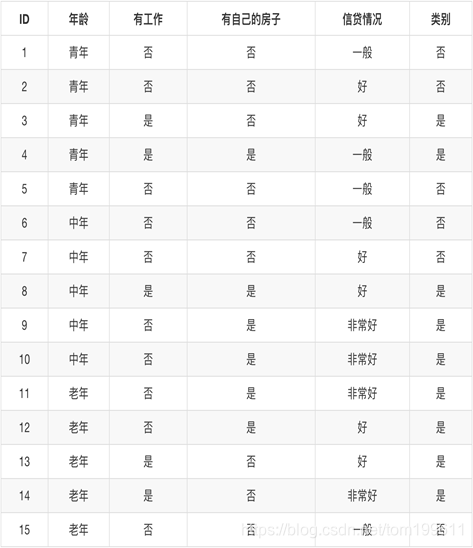
在这里插入图片描述

`初始信息熵`：只看目标值。是（9/15）和否（6/15）

`初始信息熵` = -1 （9/15log 9/15+6/15* log 6/15 ）

`年龄信息熵` :青年（5 / 15）中年（5 / 15）老年（5 / 15）

年龄信息熵 = -1 * [ 5/15 * H(青年) + 5/15 * H(中年)+5/15 * H（老年） ]

H(青年) = -1 (2/5log 2/5 + 3/5*log 3/5)

决策树：把信息增益越大的（不确定性下降越大的特征）放在树的越前面。

api :

from sklearn.tree import DecisionTreeClassifier
DecisionTreeClassifier(criterion=’gini’, max_depth=None,random_state=None)

criterion: 默认是’gini’系数，也可以选择信息增益’entropy’

max_depth:树的深度大小，

代码

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.feature_extraction import DictVectorizer
def decision_tree

最低0.47元/天解锁文章

sklearn -分类算法 -决策树

信息熵（香农提出）

信息增益 ：

初始信息熵： 只看目标值 。是（9/15）和否（6/15）

初始信息熵 = -1 （9/15log 9/15+6/15* log 6/15 ）

年龄信息熵 :青年（5 / 15） 中年（5 / 15） 老年（5 / 15）

决策树：把信息增益 越大的（不确定性下降越大的特征）放在树的越前面。