算法挑战：星球旅行、跑步路线、砝码称重与环境治理-优快云博客

本文链接：https://blog.youkuaiyun.com/tireudy/article/details/128707533

巩固

汤姆斯的天堂梦

题目描述

汤姆斯生活在一个等级为 $0$ 的星球上。那里的环境极其恶劣，每天 $12$ 小时的工作和成堆的垃圾让人忍无可忍。他向往着等级为 $N$ 的星球上天堂般的生活。

有一些航班将人从低等级的星球送上高一级的星球，有时需要向驾驶员支付一定金额的费用，有时却又可以得到一定的金钱。

汤姆斯预先知道了从 $0$ 等级星球去 $N$ 等级星球所有的航线和需要支付（或者可以得到）的金钱，他想寻找一条价格最低（甚至获得金钱最多）的航线。

输入格式

第一行一个正整数 $N$ （ $\le 100$ ），接下来的数据可分为 $N$ 个段落，每段的第一行一个整数 $K_i$ （ $Ki≤100K_i \le 100$ ），表示等级为 $i$ 的星球有 $K_i$ 个。

接下来的 $K_i$ 行中第 $j$ 行依次表示与等级为 $i$ ，编号为 $j$ 的星球相连的等级为 $i - 1$ 的星球的编号和此航线需要的费用（正数表示支出，负数表示收益，费用的绝对值不超过 $1000$ ）。

每行以 $0$ 结束，每行的航线数 $≤100\le 100$ 。

输出格式

输出所需（或所得）费用。正数表示支出，负数表示收益。

样例 #1

样例输入 #1

3
2
1 15 0
1 5 0
3
1 -5 2 10 0
1 3 0
2 40 0
2
1 1 2 5 3 -5 0
2 -19 3 -20 0

样例输出 #1

-1

提示

对于 $\%$ 的数据， $\le N \le 100$ ， $\le K_i \le 100$ 。

样例解释：

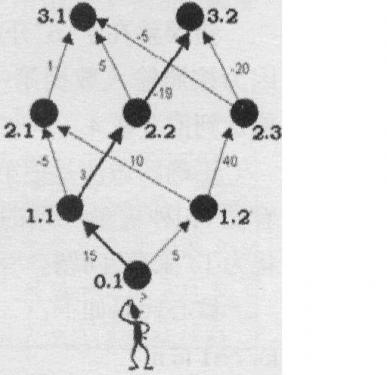
代码

#include<cstdio>
#include<climits>
using namespace std;
int f[200][200]={0};
int main()
{
    int n,a;
    scanf("%d",&n);
    for(int i=1;i<=n;++i)
    {
        scanf("%d",&a);
        for(int j=1;j<=a;++j)
        {
            f[i][j]=INT_MAX-1000;
            int b,c;
            scanf("%d",&b);
            while(b!=0)
            {
                scanf("%d",&c);
                f[i][j]=f[i-1][b]+c<f[i][j]?f[i-1][b]+c:f[i][j];//DP
                scanf("%d",&b);
            }
        }
    }
    int min=INT_MAX;
    for(int i=1;i<=a;++i)
        min=f[n][i]<min?f[n][i]:min;
    printf("%d",min);
    return 0;
}

跑步

题目描述

路人甲准备跑 $n$ 圈来锻炼自己的身体，他准备分多次（ $>1\gt1$ ）跑完，每次都跑正整数圈，然后休息下再继续跑。

为了有效地提高自己的体能，他决定每次跑的圈数都必须比上次跑的多。

可以假设他刚开始跑了 $0$ 圈，那么请问他可以有多少种跑完这 $n$ 圈的方案？

输入格式

一行一个整数，代表 $n$ 。

输出格式

一个整数表示跑完这 $n$ 圈的方案数。

样例 #1

样例输入 #1

样例输出 #1

995645335

提示

数据规模与约定

对于 $100%100\%$ 的数据，保证 $5≤n≤5005\le n\le 500$ 。

代码

#include<bits/stdc++.h>
using namespace std;
long long n,ans[501]; 
int main(){
    scanf("%d",&n);
    ans[0]=1;
    for (int i=1;i<=n;i++){
    	for (int j=n;j>=i;j--){
    		ans[j]+=ans[j-i];
		}
	}
	cout<<ans[n]-1<<endl;
    return 0;
}

[蓝桥杯 2021 省 AB] 砝码称重

题目描述

你有一架天平和 $N$ 个砝码, 这 $N$ 个砝码重量依次是 $,WNW_{1}, W_{2}, \cdots, W_{N}$ 。请你计算一共可以称出多少种不同的重量?

注意砝码可以放在天平两边。

输入格式

输入的第一行包含一个整数 $N$ 。

第二行包含 $N$ 个整数: $,WNW_{1}, W_{2}, W_{3}, \cdots, W_{N}$ 。

输出格式

输出一个整数代表答案。

样例 #1

样例输入 #1

3
1 4 6

样例输出 #1

提示

【样例说明】

能称出的 10 种重量是: $1 、 2 、 3 、 4 、 5 、 6 、 7 、 9 、 10 、 11$ 。

$\begin{aligned} &1=1 \\ &2=6-4(\text { 天平一边放 } 6, \text { 另一边放 4) } \\ &3=4-1 \\ &4=4 \\ &5=6-1 \\ &6=6 \\ &7=1+6 \\ &9=4+6-1 \\ &10=4+6 \\ &11=1+4+6 \end{aligned}$

【评测用例规模与约定】

对于 $\%$ 的评测用例, $\leq N \leq 15$ 。

对于所有评测用例, $\leq N \leq 100, N$ 个砝码总重不超过 $10^5$ 。

蓝桥杯 2021 第一轮省赛 A 组 F 题（B 组 G 题）。

代码

#include <bits/stdc++.h>
using namespace std;
int dp[100010], a[110];
long long sum = 0, ans = 0;
int main()
{
	int n;
	cin >> n;
	fill(dp, dp + 100010, 0);
	dp[0] = 1;
	for (int i = 0; i < n; i++)
		cin >> a[i], sum += a[i];
	for (int i = 0; i < n; i++){
		for (int j = sum; j >= a[i]; j--){ 
			if (dp[j - a[i]] == 1 and dp[j] != 1)
				dp[j] = 1, ans++;
		}
	}
	for (int i = 0; i < n; i++){
		for (int j = 1; j <= sum - a[i]; j++){ /
			if (dp[j + a[i]] == 1 and dp[j] == 0)
					dp[j] = 1, ans++;
		}
	}
	cout << ans;
	return 0;
}

遗址

题目描述

很久很久以前有一座寺庙，从上往下看寺庙的形状正好是一个正方形，由 $4$ 个角上竖立的圆柱搭建而成。现在圆柱都倒塌了，只在地上留下圆形的痕迹，可是现在地上有很多这样的痕迹，专家说一定是最大的那个。

写一个程序，给出圆柱的坐标，找出由 $4$ 个圆柱构成的最大的正方形，因为这就是寺庙的位置，要求计算出最大的面积。注意正方形的边不一定平行于坐标轴。

例如图有 $10$ 根柱子，其中 $(4, 2), (5, 2), (5, 3), (4, 3)$ 可以形成一个正方形， $(1, 1), (4, 0), (5, 3), (2, 4)$ 也可以，后者是其中最大的，面积为 $10$ 。

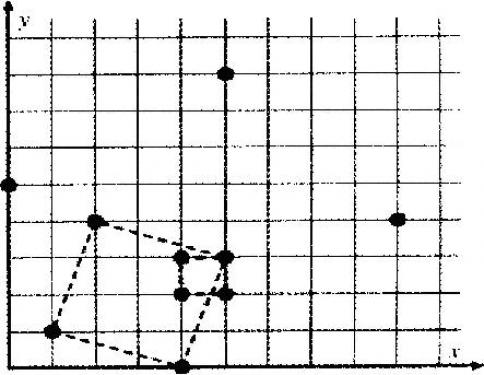
输入格式

第一行包含一个 $N(1≤N≤3000)N(1\leq N\leq 3000)$ ，表示柱子的数量。

接下来 $N$ 行，每行有两个空格隔开的整数表示柱子的坐标（坐标值在 $0$ 到 $5000$ 之间），柱子的位置互不相同。

输出格式

如果存在正方形，输出最大的面积，否则输出 $0$ 。

样例 #1

样例输入 #1

样例输出 #1

提示

【数据范围】

$30%30\%$ 满足： $1≤N≤1001\leq N \leq100$ 。

$60%60\%$ 满足： $1≤N≤5001\leq N \leq500$ 。

$100%100\%$ 满足： $1≤N≤30001\leq N \leq3000$ 。

代码

#include<bits/stdc++.h>
#define max(a,b) a>b?a:b
using namespace std;
bool f[5020][5020];
int x[3020];
int y[3020];
int n,m;
int main()
{
//	freopen("ruin.in","r",stdin);
//	freopen("ruin.out","w",stdout);
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%d%d",x+i,y+i);
		f[x[i]][y[i]]=1;
	}
	int ans=0;
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=n;j++)
		{
			
			int a=x[i]-x[j];
			int b=y[i]-y[j];
			int Ax=x[i]-b;
			int Bx=x[j]-b;
			int Ay=y[i]+a;
			int By=y[j]+a;	
            if(Ax<1||Ax>5000||Bx<1||Bx>5000||Ay<1||Ay>5000||By<1||By>5000)continue;
			if(f[Ax][Ay]&&f[Bx][By])
			{
				ans=max(ans,a*a+b*b);
			}
		}
	}
	printf("%d\n",ans);
    return 0;
}

[蓝桥杯 2022 国 A] 环境治理

题目描述

LQ 国拥有 $n$ 个城市，从 $0$ 到 $n - 1$ 编号，这 $n$ 个城市两两之间都有且仅有一条双向道路连接，这意味着任意两个城市之间都是可达的。每条道路都有一个属性 $D$ ，表示这条道路的灰尘度。当从一个城市 A 前往另一个城市 B 时，可能存在多条路线，每条路线的灰尘度定义为这条路线所经过的所有道路的灰尘度之和，LQ 国的人都很讨厌灰尘，所以他们总会优先选择灰尘度最小的路线。

LQ 国很看重居民的出行环境，他们用一个指标 $P$ 来衡量 LQ 国的出行环境， $P$ 定义为：

$P=∑i=0n−1∑j=0n−1d(i,j)P=\sum \limits_{i=0}^{n-1} \sum \limits_{j=0}^{n-1} d(i,j)$

其中 $d (i, j)$ 表示城市 $i$ 到城市 $j$ 之间灰尘度最小的路线对应的灰尘度的值。

为了改善出行环境，每个城市都要有所作为，当某个城市进行道路改善时，会将与这个城市直接相连的所有道路的灰尘度都减少 $1$ ，但每条道路都有一个灰尘度的下限值 $L$ ，当灰尘度达到道路的下限值时，无论再怎么改善，道路的灰尘度也不会再减小了。

具体的计划是这样的：

第 $1$ 天， $0$ 号城市对与其直接相连的道路环境进行改善；
第 $2$ 天， $1$ 号城市对与其直接相连的道路环境进行改善；

……

第 $n$ 天， $n - 1$ 号城市对与其直接相连的道路环境进行改善；
第 $n + 1$ 天， $0$ 号城市对与其直接相连的道路环境进行改善；
第 $n + 2$ 天， $1$ 号城市对与其直接相连的道路环境进行改善；

……

LQ 国想要使得 $P$ 指标满足 $\leq Q$ 。请问最少要经过多少天之后， $P$ 指标可以满足 $\leq Q$ 。如果在初始时就已经满足条件，则输出 $0$ ；如果永远不可能满足，则输出 $- 1$ 。

输入格式

输入的第一行包含两个整数 $n, Q$ ，用一个空格分隔，分别表示城市个数和期望达到的 $P$ 指标。

接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $D_{i,j} (D_{i,j}=D_{j,i},D_{i,i} = 0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度。

接下来 $n$ 行，每行包含 $n$ 个整数，相邻两个整数之间用一个空格分隔，其中第 $i$ 行第 $j$ 列的值 $L_{i,j} (L_{i,j} = L_{j,i}, L_{i,i} = 0)$ 表示城市 $i$ 与城市 $j$ 之间直接相连的那条道路的灰尘度的下限值。

输出格式

输出一行包含一个整数表示答案。

样例 #1

样例输入 #1

样例输出 #1

提示

【样例说明】

初始时的图如下所示，每条边上的数字表示这条道路的灰尘度：

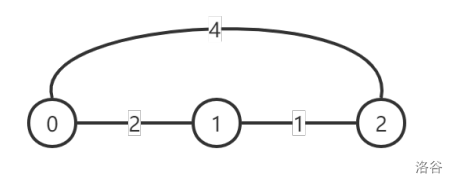
此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

$d (0, 0) = 0, d (0, 1) = 2, d (0, 2) = 3$ ；
$d (1, 0) = 2, d (1, 1) = 0, d (1, 2) = 1$ ；
$d (2, 0) = 3, d (2, 1) = 1, d (2, 2) = 0$ 。

初始时的 $P$ 指标为 $\times 2 = 12$ ，不满足 $\leq Q = 10$ ;

第一天， $0$ 号城市进行道路改善，改善后的图示如下：

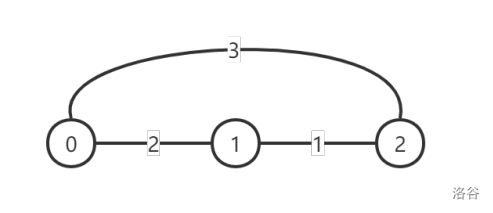
注意到边 $(0, 2)$ 的值减小了 $1$ ，但 $(0, 1)$ 并没有减小，因为 $L_{0,1} = 2$ ，所以 $(0, 1)$ 的值不可以再减小了。此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

$d (0, 0) = 0, d (0, 1) = 2, d (0, 2) = 3$ ，
$d (1, 0) = 2, d (1, 1) = 0, d (1, 2) = 1$ ，
$d (2, 0) = 3, d (2, 1) = 1, d (2, 2) = 0$ 。

此时 $P$ 仍为 $12$ 。

第二天，1 号城市进行道路改善，改善后的图示如下：

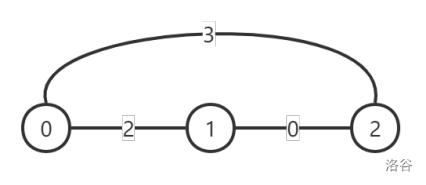
此时每对顶点之间的灰尘度最小的路线对应的灰尘度为：

$d (0, 0) = 0, d (0, 1) = 2, d (0, 2) = 2$ ，
$d (1, 0) = 2, d (1, 1) = 0, d (1, 2) = 0$ ，
$d (2, 0) = 2, d (2, 1) = 0, d (2, 2) = 0$ 。

此时的 $P$ 指标为 $\times 2 = 8 < Q$ ，此时已经满足条件。

所以答案是 $2$ 。

【评测用例规模与约定】

对于 $30%30\%$ 的评测用例， $\leq n \leq 10$ ， $\leq L_{i,j} \leq D_{i,j} \leq 10$ ；
对于 $60%60\%$ 的评测用例， $\leq n \leq 50$ ， $\leq L_{i,j} \leq D_{i,j} \leq 10^5$ ；
对于所有评测用例， $\leq n \leq 100$ ， $\leq L_{i,j} \leq D_{i,j} \leq 10^5$ ， $\leq Q \leq 2^{31} - 1$ 。

蓝桥杯 2022 国赛 A 组 F 题。

代码

#include<bits/stdc++.h>
#define int long long
using namespace std;
int x[101][101],dis[101][101],diss[101][101];
int n,m;
int cheak(int k){
	int p=k/n,o=k%n;
	for(int q=1;q<=n;q++){//更新边权
		for(int w=1;w<=n;w++){
			diss[q][w]=max(dis[q][w]-p,x[q][w]);
			if(o>=q)diss[q][w]=max(diss[q][w]-1,x[q][w]);
		}
	}
	int ans=0;
	for(int k=1;k<=n;k++){//Floyd板子
		for(int q=1;q<=n;q++){
			for(int w=1;w<=n;w++){
				diss[q][w]=min(diss[q][w],diss[q][k]+diss[k][w]);
			}
		}
	}
	for(int q=1;q<=n;q++){
		for(int w=1;w<=n;w++)
			ans+=diss[q][w];
	}
	if(ans<=m)return 1;
	return 0;
}
inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=(x<<3)+(x<<1)+ch-48;ch=getchar();}
	return x*f;
}
signed main(){
	n=read();m=read();
	for(int q=1;q<=n;q++){
		for(int w=1;w<=n;w++)
			dis[q][w]=read();
	}
	for(int q=1;q<=n;q++){
		for(int w=1;w<=n;w++)
			x[q][w]=read();
	}
	int p=0;
	for(int k=1;k<=n;k++){
		for(int q=1;q<=n;q++){
			for(int w=1;w<=n;w++){
				dis[q][w]=min(dis[q][w],dis[q][k]+dis[k][w]);
			}
		}
	}
	for(int q=1;q<=n;q++){
		for(int w=1;w<=n;w++)
			p+=dis[q][w];
	}
	if(p<=m){
		cout<<"0";
		return 0;
	}
	int l=1,r=1e6;
	while(l<=r){
		int mid=(l+r)>>1;
		if(cheak(mid)==1)r=mid-1;
		else l=mid+1;
	}
	if(l==1e6+1){
		cout<<"-1";
		return 0;
	}
	cout<<l;
	return 0;
}
}
	for(int q=1;q<=n;q++){
		for(int w=1;w<=n;w++)
			x[q][w]=read();
	}
	int p=0;
	for(int k=1;k<=n;k++){
		for(int q=1;q<=n;q++){
			for(int w=1;w<=n;w++){
				dis[q][w]=min(dis[q][w],dis[q][k]+dis[k][w]);
			}
		}
	}
	for(int q=1;q<=n;q++){
		for(int w=1;w<=n;w++)
			p+=dis[q][w];
	}
	if(p<=m){
		cout<<"0";
		return 0;
	}
	int l=1,r=1e6;
	while(l<=r){
		int mid=(l+r)>>1;
		if(cheak(mid)==1)r=mid-1;
		else l=mid+1;
	}
	if(l==1e6+1){
		cout<<"-1";
		return 0;
	}
	cout<<l;
	return 0;
}