基于几何嵌入的电路逆向工程

通过电路图的几何嵌入逆向工程数字集成电路

1 引言

在由多个供应商参与且电路设计与制造均处于不可信供应链环境中的情况下，检测设计中的恶意更改变得十分困难。通过逆向工程重构高层功能是一种有助于揭示此类更改的重要技术。

一项初步工作 [19] 研究了著名的ISCAS‐85电路，并从门级网表出发，提供了供人工分析人员审查的高层模块识别技术。这些技术包括寻找共享的控制功能、全局线（如时钟或复位信号）、发现重复的电路片段和库模块、从重复模块的输出中识别总线结构，以及利用网表中出现的常用名称。

参考文献中提出的方法 [24, 34] 侧重于对一组库组件与扁平门级电路进行功能匹配的自动技术。在匹配技术方面，这些文章与之前基于模板的电路理解领域的研究相似，使用逻辑等价和模型检测方法 [15, 25, 27]。还有一些方法致力于从设计的反馈回路中识别给定网表中的有限状态机（FSMs）[32]，但这些匹配技术并不完整，也无法匹配复杂组件，导致测试电路的大部分未被匹配。

另一个最近的研究尝试是将电路的某些部分与一组预定义的库组件进行匹配，该方法采用子图同构算法在给定的子电路中查找组件 [33]。通过选择一组可能的输入输出模式，他们分别为待搜索的电路模块和候选组件构建图。他们并不进行逻辑分析，而是建议一种可能的匹配，随后由等价性检查器进行分析。该方法的准确性和复杂度取决于用于构建图的仿真向量集合以及库组件和给定子电路对应图的大小。正如作者在文章中提到的，初始子电路识别仍然是一个有待解决的问题。

除了子电路匹配算法外，也有研究利用基于聚类的技术实现自动电路划分 [3–6, 10, 11, 14, 17, 18, 29, 31]。关于这类方法的文章采用了不同的算法，大多是基于图的算法，从随机游走到谱分解不等，以将电路划分为互不相交的簇。为此已研究了多种布局算法。然而，这些技术并未提供一种在设计的两个不同版本之间进行高层级模块匹配的算法。

逆向工程中的主要挑战是基于结构信息在大量逻辑门中找到有意义的组件边界。据我们所知，以往的技术均未提出对电路进行高层模块全局划分的方法，而我们的方法是首个成功实现高准确率识别设计大规模划分的方案。诸如基于谱聚类的算法等划分技术 [5, 17] 能够识别电路划分，但并未解决将这些簇与参考模型中的行为模块进行匹配的问题。在本研究中，我们探讨了这样一种情况：电路的初始行为或寄存器传输级（RTL）描述是已知的，我们需要为从制造环节获得的设计（即测试电路）找出与其行为/RTL模块划分相对应的有意义的功能划分。我们采用图嵌入方法来应对这一问题。对于参考电路和测试电路，我们分别计算一个 $d^ $ 维几何嵌入，使得电路中的每根线对应于相应 $d^ $ 维空间中的一个点。

经过向量对齐步骤（如必要）后，我们使用二分匹配算法来寻找测试电路与参考电路节点之间的对应关系。该算法的最终输出是利用原始设计中已知的模块划分，为测试电路中的每根线提供标记。随后可进行验证步骤，借助自动化技术并可能由人工分析员辅助，验证测试电路划分中的各个模块是否与参考电路的模块相匹配。此验证步骤不在本文讨论范围之内。我们不进行任何逻辑等价检查，也不考虑设计中门电路的逻辑/类型以实现功能验证。

我们的工作提出了一种不同于以往探索策略的新型逆向工程问题解决方案。它有助于设计工程师自动推断出不可信电路的高层表示，并为上述技术提供了一种补充工具。在大型开源处理器OpenSparc T1上的实验结果表明，该算法的有效性可达最高99%的匹配准确率，覆盖率达到92%。

2 提出的方法

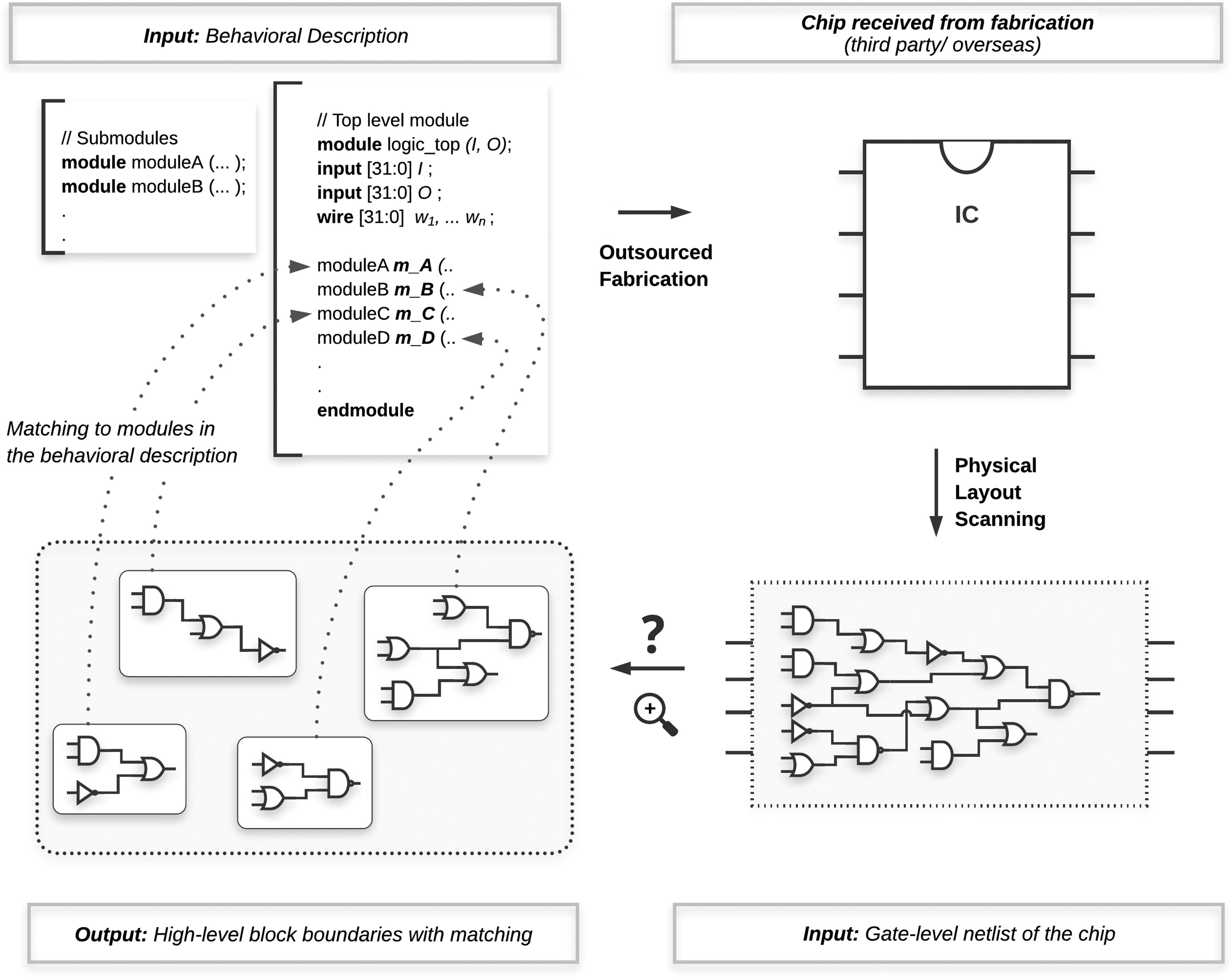
我们研究了逆向工程中的功能划分问题，目标是对从制造环节获得的集成电路进行高层级模块划分。图1展示了我们解决方案的概览。我们假设原始设计以某种硬件描述语言（HDL）存在，表现为行为级或RTL源代码，可通过综合得到门级电路，该电路被称为参考电路。我们还假设已获得不可信的制造设计，即测试电路，其同样以门级网表形式存在并可进行分析。在测试电路中识别出与参考设计相对应的高层级模块，有助于揭示在设计与生产流程中插入的恶意更改。我们的方法提出了一种新颖的技术，利用了设计者已掌握的有用信息：参考HDL设计中的高层级模块。逆向工程的功能划分旨在将测试设计中的门电路标记为它们可能所属的参考HDL中的高层级模块。这种标记提供了测试电路的划分，使得每个划分均可独立进行分析，甚至可与其对应的高层级模块进行验证。本文的重点在于划分和标记。分析/验证可采用已知技术 [34] 完成，不在本文讨论范围内。我们的工作应与一种精细匹配技术，可将其用作恶意插入的检测工具。（在我们的威胁模型中，我们不对 CAD工具做任何假设。由于设计工程师可以选择不同的CAD工具进行设计综合，并通过比较从每个此类工具获得的不同网表来检查结果，因此我们的算法提供了一种稳健的方法，用于识别具有可比输出的高层级模块。如果设计者对其所使用的CAD工具的可信度不确定，则其可以将当前工具与其他工具结合使用，以获得不同的参考图，并检查每个输出，从而验证测试电路中由不同参考图勾勒出的大致边界。我们希望就此问题提出一些建议，供那些有兴趣使用我们算法但无法获得可信综合工具的读者参考。） 请注意，攻击者仍可能在模块内部插入恶意电路。这促使我们需要进一步研究，以检测我们匹配技术所识别出的模块内部的恶意插入。我们的匹配算法仍然有用，因为它有助于识别出更小的模块，以便进一步分析。

该提出的方法利用两个功能相似的设计（即参考电路和测试电路）之间的图相似性，并输出两组电路之间的对应关系。我们算法的步骤总结如下：

步骤 1 ：如果需要，通过综合设计描述以获得扁平网表，从而为参考设计准备门级电路。[参考网表]

步骤 2 ：然后，使用参考电路和测试电路的扁平网表获取相应的电路图。[电路图]

步骤 3 ：接下来，计算图中所有节点的几何嵌入。这提供了一种数学表示，使我们能够在低维空间中比较两个电路的节点。[geometric embedding]

步骤 4 ：然后对嵌入坐标进行坐标对齐，以计算两个网表中门电路之间的二分分配，从而建立两个电路之间的节点对应关系。[坐标对齐]

步骤 5 ：参考电路中的门电路被标记为其所属的高级模块。在下一步中，将计算二分匹配。利用参考设计中的标签来确定测试电路中相应的功能单元。[二分匹配/节点标记]

步骤 6 ：由于分配结果可能存在噪声，我们加入最终清理阶段。然后，提供测试设计的高层级表示作为输出。[清理阶段]

A. 嵌入与特征提取（步骤 [1–4]）

对于嵌入阶段，我们建议采用两种替代算法来计算节点的特征，这些特征随后可以合并成更丰富的特征集，以用于最终匹配：特征分解和基于主输入/输出的特征。

1.1. 基于特征分解的特征（步骤 [1–3]）

第一种嵌入方法基于电路图的特征分解。因此，需要获取网表的图表示。如果参考设计以硬件描述语言源代码形式提供，则需将其综合以获得扁平门级网表。因此，在此阶段之后，假设参考设计和测试电路均处于门级。图 2展示了一个逻辑布线示例及其对应的电路图 Gx（V, E），其中每条线由 V 中的一个顶点表示，而来自 E 的一条边表示逻辑组件 [9] 的输入‐输出关系。优先选择无向图，因为我们希望捕捉节点之间的功能关系，而不受方向影响。然后，这些边

图中的节点根据其连接性被赋予一个相似性权重。设 $\Gamma(x_p)$ 表示节点 $x_p$ 及其所有相邻顶点的邻域，使得 $\Gamma(x_p) = {x_t \in V | {x_p, x_t} \in E}$，节点 $x_p$ 和 $x_q$ 之间的相似性 $s(x_p, x_q)$ 定义如下：

$$
s(x_p , x_q)= \frac{1}{\sqrt{|\Gamma(x_p)|}\sqrt{|\Gamma(x_q)|}}. \tag{1}
$$

该归一化步骤检查每个节点的度，并调整边上的权重以反映邻居之间的图相似性。通过为作为不同簇之间桥梁的节点（由于节点的高顶点度）以及与图的稠密部分弱连接的节点（由于邻居的高顶点度）增加分母，有助于降低图中枢纽和离群点之间边的权重。

接下来，基于邻接表和每个顶点的k近邻{k‐nearest neighbors} $\Gamma_k(x_p)$ 构建相似性矩阵。在计算最近邻时，定义每个顶点 $x_p$ 与其相邻顶点 $x_q \in \Gamma(x_p)$ 之间的距离为对应相似性值 $s(x_p, x_q)$ 的倒数。对于非相邻顶点 $x_p$ 和 $x_t$，若 $x_t \notin \Gamma(x_p)$ 但 $x_p$ 通过多条边 $x_p \to x_t$ 与 $x_t$ 相连，则它们之间的距离被计算为连接它们的最短路径上的距离之和。节点到自身的距离定义为 0。完成邻居计算后，通过可能的添加操作调整集合，以获得对称矩阵。图3展示了通过设置 $k = 3$ 为图2中的示例电路构造的相似性矩阵。矩阵中的值表示节点的接近度，即对应路径距离的倒数。矩阵中用1表示的条目代表实际邻接关系，而圆点表示具有高权重的k个最近邻。

相似性矩阵帮助我们定义逻辑中的功能组。矩阵中的簇由图中节点（线）之间的相似性定义，而非线之间的绝对路径，而是它们的连通性。因此，在下一步中，我们需要一种方法，能够识别这些高相关性区域，而不论矩阵中节点的顺序如何。特征分解提供了一种数学框架，将矩阵分解为标准形式，使其可以用满足以下方程的特征对（$\lambda_e$，$v_e$）表示：

$$
A v_e= \lambda_e v_e, \tag{2}
$$

其中 $A$ 表示相似性矩阵，$v_e$ 代表其对应特征值为 $\lambda_e$ 的特征向量。如果相似性矩阵是对称的（在我们的情况下由于无向边构造成立），则特征向量构成一个标准正交基 [22]，因此每一行（或列）都可以表示为其特征向量的线性组合： $\sum_i \alpha_i v_{ei}$。从图 3 可以看出，可能在线性组合中具有高系数、用于逼近矩阵行的期望特征向量，很可能呈现在右侧所示向量的形式中，其中再次强调，用1标记的区域相比其余部分具有较高值。矩阵中每个簇的节点所对应的行可以通过将其中一个特征向量作为基，并对其他向量使用小系数，在方程求和中根据该行的具体值进行调整来构造。因此，一个簇中的节点可以使用相应特征向量行中的值进行编码。例如，电路中的节点Y，仅考虑主特征向量而忽略其余向量时，可编码为 <0， 0， 1>，这使我们获得了一个相对于矩阵大小而言维度较小的嵌入（d= 3）。

总体而言，使用矩阵分解技术的主要思想基于上述洞察。然而，在构建初始矩阵以及确定用于嵌入的特征向量数量时，还涉及更多的数学运算。在我们的方法中，我们采用了吴等人[28]提出的NJW算法，从相似性矩阵构造归一化拉普拉斯矩阵，并获取特征。由于我们的矩阵是对称的，且仅需要一定数量的向量，因此我们所需的计算是一种特殊的计算，称为截断对称特征值分解，该分解仅获得前d个最小（或最大）的d正交特征向量。该计算的复杂度取决于方阵的行数以及嵌入维度（d）的估计值，对于稀疏矩阵而言，计算速度可以非常快[16, 23]。通过检查分解后的特征值来识别主特征向量。我们在第3节末尾解释实验结果时，将讨论如何确定这些特征向量及其数量。3同时解释我们的实验结果。

让图 2中的逻辑门表示我们的参考设计，而我们在图 4中使用低级技术库综合出一个测试电路。该测试电路通过更基本的门电路实现了相同的功能，并提供了如图 Gy 所示的电路图 5。观察此电路图可知，如果我们计算该新电路的节点亲和性，则相应的矩阵将具有与图3中相同的骨架结构，且主特征向量的形状与参考设计的主特征向量相似，从而在两个电路的节点之间产生可比较的嵌入结果。因此，尽管这些电路的图并不完全相同，但它们之间的相似性体现在矩阵分解的结果中。

图6。一个小型二维示例，其中三角形和星号点表示来自不同电路的节点，而e1、e2和f1、f2是用于帮助可视化特征向量嵌入的虚拟投影轴。

乍一看，特征向量可以被视为一种类似于比割划分技术的方法，用于区分给定图中的局部簇。然而，与局部搜索方法相比，特征向量能够提供更好的结果，并为大规模优化问题提供全局视图，避免陷入局部极小值。对于我们的目的而言，特征向量更为可取，因为我们希望在两个电路之间建立一个可比较的坐标系，而不是基于节点连接性的聚类方法——这种聚类可能输出的簇粒度与我们期望的不同。特征向量使我们能够实现引导式划分：根据参考电路对簇进行标记，并利用坐标计算匹配，而无需考虑电路图中簇的层次结构，从而能够控制划分的数量和形状。

在我们的算法中，我们使用每次嵌入中的正交特征向量来近似一个d维空间（d‐space）的线性跨度 $d \leq d_1$ 以及 $d \leq d_2$，其中 $d_1$ 和 $d_2$ 分别表示参考电路和测试电路分解中向量的数量。我们的方法不要求初始嵌入的维度 $d_1$ 和 $d_2$ 相等。对应的特征向量 $v_{ek}, 1 \leq k \leq d_1$ 和 $v_{fl}, 1 \leq l \leq d_2$ 也可能具有不同的形状 $m \times 1$ 和 $n \times 1$，这取决于参考电路和测试电路的规模。因此，我们需要一个预处理步骤来调整嵌入坐标以便进行比较。为此，首先从每个特征向量中减去其均值，使得坐标轴上的值在两个嵌入中均以原点为中心。然后，我们采用一个更正式的调整步骤来寻找轴之间的对应关系。该技术的详细信息如下所述。

1.2. 特征对齐（步骤4）

图6显示了一个二维示例，其中三角形点表示第一个电路的节点，而星号点表示另一组节点。e1, e2和f 1, f 2分别是两个嵌入的轴。在我们的方法中，并不实际进行轴的计算，而是从特征嵌入步骤中获得这些轴上点的投影。例如，对于第一个电路，特征向量 $v_{e1}$ 和 $v_{e2}$ 包含的值表示节点相对于e1和e2的节点位置。以下的轴是假想的组成部分，帮助我们理解特征向量上的值。

我们为每个图计算出的特征向量给出了两个独立的向量集，它们张成相同的坐标空间。基于两个电路具有相似功能的假设，我们

假设它们大致覆盖相同的空间。然而，这并不一定意味着它们是相互对齐的，且两种表示之间每个轴都存在对应关系。尽管我们尝试通过从每个特征向量中减去其均值来将其围绕零点居中，但由于数据存在噪声，两组数据的质心可能并不对齐。如前所述，每个嵌入的向量数量和大小也可能不同，$m \times 1$ 和 $n \times 1$，具体取决于每个图中的节点数量。即使大小相等，一个向量集中的某个特征向量也可能是另一个向量集中若干特征向量的线性组合。

然而，为了获得可比较的几何编码，需要一个变形步骤，以确保嵌入轴围绕相同的均值居中、角度对齐，并按比例缩放。在没有其他额外信息的情况下，仅基于给定的两个向量集，该问题通常没有简单的解决方案。

我们额外知道的信息是，某些具有固定匹配对应关系的节点的嵌入坐标：即设计中的输入/输出（I/O）引脚。根据我们对电路的相似性假设，我们知道每个嵌入中的特征向量代表了我们的d维空间中的两个不同的张成集合，也就是说，通过其中一个集合中向量的线性组合，我们可以构造（在我们的情况下是近似构造，由于特征向量选择有限）d维空间内的任意向量。利用这两条信息，我们提出了以下特征调整方法。

对于每一组，我们首先构建一个新的矩阵，其中矩阵的行表示I/O引脚，列表示来自特征向量的值，即这些节点的嵌入坐标。因此，如果有r个不同的I/O引脚，我们构造一个 $r \times d_1$ 和 $r \times d_2$ 的矩阵，并保持相同的I/O行顺序。矩阵中的列是每个嵌入中特征向量的一个子集，具有不同的值。然而，根据我们之前的假设，我们知道第一个矩阵中的某一列也可以表示为第二个矩阵各列的线性组合。因此，对于第一个矩阵中的每一列 $v_k$，我们计算一组系数 $\lambda_{k,i}$，用于乘以第二个矩阵的列 $u_i, i= 1, 2, …, d_2,$，并为第一组中的向量构造一个近似值 $v^*_k$。

$$
\mathbf{v}^* k = \sum {i=1}^{d_2} \lambda_{k,i} \mathbf{u}_i, \quad k= 1, 2,…, d_1. \tag{3}
$$

因此，这是一个表述清晰的优化问题，即一个具有r个样本（训练集大小）和 $d_2$ 个变量的多元线性回归问题。对于索引为t的行，我们有元组 ${\mathbf{v} {k,t}: \mathbf{u} {1,t}, \mathbf{u} {2,t}, …, \mathbf{u} {d_2,t}}_{t=1}^r$，其中第一项为被解释变量（输出），其余为该优化问题的解释变量（输入）。

计算出系数后，我们可以为第一个系统中的每个 $v_k$ 建立对应关系，并对齐第二个矩阵中每一轴（列）上的值。为了调整原始嵌入中所有节点的值，我们遵循上述所描述的精确过程。但现在，我们将计算出的系数应用于特征向量本身，而不是I/O引脚，并将方程 (3)中的 $u_i$ 替换为其对应的特征向量。各轴被平移、旋转并使其相互平行。最后，我们将每一行归一化至范数1，以重复上述NJW算法中的最后一步 [28]。对于第一组中的每个 $v_{ek}$，我们现在在第二个嵌入中都有一个对应的特征向量 $v^*_{ek}$。

上述计算提出了一种为测试设计找到维度为 $d_1$ 的对齐的特征集的方法。因此，嵌入的最终大小 $d$ 被设置为 $d_1$，并且根据第一次嵌入的特征值来测量特征向量主导性，因为向量对齐是以其作为对齐基准进行的。（我们倾向于选择参考电路作为第一组，以便对齐基准是根据原始设计完成的。然而，反过来操作也能得到类似的近似结果。

来自特征分解的两个坐标系表示为 $Y = [\mathbf{v}^ _{e1}, \mathbf{v}^ {e2}, …, \mathbf{v}^* {ed}] {n\times d}$ 和 $X = [\mathbf{v} {e1}, \mathbf{v} {e2}, …, \mathbf{v} {ed}] {m\times d}$。前者是我们的测试电路的嵌入，后者是参考设计的嵌入。该表示中的每一行包含节点的嵌入坐标（特征）。对于 $Y$ 的第 $i$ 行中的一个元素和 $X$ 的第 $j$ 行中的一个元素，其坐标写作如下： $\mathbf{y}_i=(Y {i,1}, Y_{i,2}, …, Y_{i,d})$ 和 $\mathbf{x} j=(X {j,1}, X_{j,2}, …, X_{j,d})$。每个电路中的节点数量可能不同，因此测试电路和参考设计的大小分别用 $n$ 和 $m$ 表示。

2. 基于主输入/输出的特征（步骤 [1–3],[4]）

除了电路图的谱嵌入外，我们可以利用的另一项有用信息是每个设计中的基本图连接性，即图顶点之间的距离。为了考虑这一点，对于图中的每个主输入/输出端口，我们计算其到所有其他节点的最短距离，以获得一个度量，该度量表示节点相对于电路输入/输出端口的相对位置。我们按照与X（或Y）相同的行顺序进行这些计算，以便在需要时可将其作为新的特征列附加到X（或Y）上。顶点之间的距离根据前一节中给出的k‐最近邻计算定义来计算，但在有向图上进行。之前给出的归一化公式被以下相似性度量所替代：

$$
s_{p\to q}(x_p, x_q)= \frac{1}{\sqrt{|\Gamma_{out}(x_p)|}\sqrt{|\Gamma_{in}(x_q)|}}, \tag{4}
$$

其中 $s_{p\to q}$ 表示从节点 $x_p$ 到 $x_q$ 的有向边的归一化权重。 $\Gamma_{out}(x_p)$ 和 $\Gamma_{in}(x_q)$ 分别表示从节点 $x_p$ 出发的出边之和以及指向节点 $x_q$ 的入边之和。尽管由于对称图的鲁棒性，我们更倾向于基于对称图获取特征特征，但在计算有向IO特征时，我们引入了来自逻辑流和门连接方向的信息。

然后，按照特征特征所解释的相同论证，对每一行进行归一化以使其具有单位长度。

对于基于I/O的嵌入，不需要对两个电路的特征进行对齐。

我们现在具有节点的可比较表示，并已准备好进入匹配阶段 e.

B. 匹配与最终标注（步骤[5和 6]）

在最终匹配阶段，我们可以单独使用特征特征，或者选择基于主输入/输出端口的最短距离计算出的特征嵌入，也可以将两者进行拼接，并利用我们拥有的所有特征在更高维度上进行匹配。无论哪种情况，节点 $y_i$ 的最终嵌入向量表示为 $\mathbf{y}^ _i$，类似地，节点 $x_j$ 由 $\mathbf{x}^ _j$ 表示。

我们提供了这三种方法的实验结果。

采用与参考文献[7],中所述方法平行的方法，接下来我们计算一个分配矩阵G以保存两个节点集之间的相似性。对于每一对 $y_i$ 和 $x_j$，根据以下高斯形式计算相似性度量：

$$
g_{ij} = \exp(-d^2_{ij} /(2\sigma^2)), \tag{5}
$$

其中 $d_{ij}$ 表示 $\mathbf{y}^ _i$ 与 $\mathbf{x}^ j$ 之间的欧几里得距离， $\sigma$ 是所有 $d {ij}$ 值的标准差。该方程的结果根据节点的d维嵌入给出了节点几何邻近性的近似值。类似于为通用机器学习技术对数据应用的预归一化步骤，此步骤有助于构建具有归一化权重的图，以提高准确性。根据该方程，两个节点之间的边如果具有

特征向量差异很大的节点被赋予较小的相似性权重，而彼此非常接近的节点（即具有非常相似特征的节点）则被赋予接近1的值。因此，我们得到了一组归一化的相似性权重。现在，我们需要求解的是两个二分集之间的最大权匹配。

图7显示了两个嵌入之间节点对应的二分图 $G(Y,X;E)$。在我们的分配矩阵中，矩阵的行对应集合Y中的节点，列表示集合X中的元素。条目是图中节点之间边的权重。由于每个集合中的元素数量不同，因此我们矩阵的大小为 $n \times m$。然而，为了获得一个平衡且完整的图，我们可以假设分配矩阵是方阵，通过在必要时添加带零权重边的虚拟节点，得到一个新的 $\tilde{n} \times \tilde{n}$ 矩阵。我们希望矩阵为方阵的原因是为了使其适用于下一阶段可用于类似指派问题的各种不同算法。

最大权匹配问题的对偶问题称为最小成本匹配，对于满足 $|X| = |Y| = \tilde{n}$ 的平衡二分图，该问题可通过匈牙利算法在多项式时间内求解。该方法是一种组合优化算法，给定一个 $\tilde{n} \times \tilde{n}$ 代价矩阵，可在 $O(\tilde{n}^3)$ 复杂度内找到最小匹配[13]。实际上，该算法的运行时间从不会接近此渐近线。在我们的工具中，我们倾向于采用Volgenant提出的用于线性分配问题的更新解决方案，其在稀疏矩阵上的运行速度可快几个数量级。（本节末尾提供了关于如何降低匹配图密度以实现稀疏表示的进一步讨论。） 在下一步中，我们将相似性矩阵转换为成本表示C，其中每个元素通过从G中的最大值减去其值得到，如下所示： $c_{ij} = \max_{i,j}(g_{ij}) - g_{ij}$。该矩阵的行代表测试电路，列表示参考设计。然后，我们在C上运行匹配算法。该算法输出一个分配结果，其中较小设计中的每个节点都被分配到参考集中的一个节点。如果测试电路中的节点数 $n$ 小于参考电路中的节点数 $m$，则我们只需忽略测试集中的虚拟节点。然而，如果 $n$ 大于 $m$，则意味着测试电路中的某些节点被分配到了参考集中的虚拟节点，因此它们没有实际的匹配项。我们将在最终清理阶段稍后为这些节点找到对应的组。

如前所述，在参考电路中，一个节点属于哪个功能模块是已知的。这是因为在从参考 HDL综合生成参考电路时，综合工具通常会将HDL模块名称作为前缀保留在线网名称上。因此，在匹配算法执行后，我们可以利用参考电路节点标记所提供的信息，获得测试电路的高层级表示。在测试电路中，节点根据其匹配到的节点标签被分组到不同的簇中。对于每个

在原始设计中的功能模块，我们在测试电路中有一组候选节点，这些节点对应于该特定功能单元。

匹配结果有时可能存在噪声，某些分配可能不正确。由于网表的尺寸差异，部分节点可能未被分配标签。对于参考电路和测试电路之间节点数量存在较大差异的电路，我们预期会出现噪声，并且当测试电路更大时，会观察到未匹配节点占主导的区域。因此，我们引入了一个清理阶段。利用测试电路的连接性，我们首先检查所有节点的k近邻邻居的已分配标签，并根据多数原则确定新的标签，同时记录每次更新，直到第一次迭代完成；然后一次性更改所有标签。我们认为，观察更广的邻域有助于我们更好地估计实际边界。在第二次及后续迭代中，我们仅检查尚未分配标签的节点——即之前提到的未匹配节点。为了避免错误标签的传播，对于较小电路或可容忍数量的未匹配节点的情况，我们跳过初始校正步骤，仅检查那些无标签的节点。该算法收敛很快，因为每次迭代后我们仅对少数剩余节点进行标签分配。（在参考设计中连接模块的中间连线所对应的节点被标记为模块之间的中间逻辑，并参与标签传播过程。结果评估同时考虑模块和中间逻辑的标签。）关于如何确定k的取值，以及如何针对大电路和较小电路选择建议的清理方法，将在下一节中说明。

一旦获得了测试电路的标记簇，我们就有效地将网表划分为高层模块。这解决了从给定测试网表的大量门电路中确定模块边界的主要问题。随后可以对测试电路中识别出的模块进行分析，甚至与参考设计中的相应模块进行比对验证[34],此步骤超出了本文的范围。

关于降低匹配算法运行时复杂度的讨论：在处理大型设计时，为了获得更好的运行时间，我们首先将原始的完全二分图（见图7）转换为稀疏表示。我们通过选择一个参数 $\rho_s$ 来减少图中的边数，该参数仅保留相似性矩阵每行和每列中的部分边，其余则忽略。在原始矩阵的每一行和每一列中，我们标记出值最高的 $\rho_s$ 个条目，并仅使用这些条目构建新的稀疏图。通过这种方式，我们去除了那些在分配算法中匹配概率较低的节点之间的边，同时保留了最相关的边。经过这一简化后，分配算法的内存消耗和复杂度均有所降低。随后，在匹配阶段，我们采用基于参考文献 [21] 中提供的琼克‐沃尔格南特算法实现，用于稠密和稀疏矩阵的 [20, 35]。

3 实验结果

我们在来自OpenCores的八个不同设计[1]以及开源多核处理器OpenSparc T1[2]上测试了我们的方法，实验平台为搭载Intel® Xeon® E5‐2680 v4 CPU（主频2.40GHz）并运行Linux 7.4的服务器（最多申请64GB内存和24个线程）。为了获得每个设计的不同实现版本，我们使用Cadence Encounter RTL编译器（RC）和Synopsys Design Compiler（DC）对它们进行综合，分别采用：(1) 针对45nm SOI工艺的IBM/ARM单元库（soi12）和 (2) Synopsys 90nm通用库（s90nm）。文中将HDL编译器称为工具A (TA) 和 工具B (TB)，工艺库则分别称为lib1（用于参考电路）和 lib2（用于测试电路）。由于学术许可协议限制，哪个（TA或TB / lib1或 lib2）对应哪个工具/库（RC或DC / soi12或 s90nm）保持匿名。这些电路还在不同的优化目标下进行了综合。参考电路使用TA针对性能（时序）进行综合，而测试设计则进行了优化

表1. 设计基准I的结果（参考‐测试/时间）[TA/lib1 ‐ TA/lib2]

表2. 设计基准II的结果（参考‐测试/面积） [TA/lib1 ‐ TA/lib2]

分别在时序和面积约束下使用工具A和工具B进行实现，得到四种不同的实现方案。为了展示该算法在不同优化目标和不同CAD工具下的电路匹配效果，我们给出了所有四种组合的结果：参考[TA/lib1] ‐ 测试/时间[TA/lib2],、参考[TA/lib1] ‐ 测试/面积[TA/lib2],、参考[TA/lib1] ‐ 测试/时间[TB/lib2]以及参考[TA/lib1] ‐ 测试/面积[TB/lib2]。作为对比，读者应注意，在我们的实验中，哪个电路称为参考电路或测试电路，以及哪个是面积优化、哪个是时间优化，都是任意指定的，因此这并不重要。正如后文将讨论的，对结果影响最大的是图的规模和连接性的差异。

对于矩阵计算和优化问题，我们使用了Armadillo和mlpack，即C++线性代数和机器学习库[12, 30]。表1、2、3和4展示了我们在各种电路上的结果摘要。第一部分提供了关于 I/O引脚数量以及每个设计对规模的信息。参考部分表示使用工具A (TA) 和lib1单元库综合的参考模型，而测试部分表示使用lib2单元库通过工具A (TA) 或工具B (TB) 进行面积或时序优化的测试设计。数据表明，参考设计与测试设计的电路图存在显著差异。例如，表1中经过时序优化的OpenSparc测试设计比参考设计多出约30,000个单元。在构建电路图时，去除了包括重复反相器对在内的缓冲结构，以帮助消除大量额外的

表3. 设计基准I的结果（参考‐测试/时间）[TA/lib1 ‐ TB/lib2]

表4. 设计基准II的结果（参考‐测试/面积） [TA/lib1 ‐TB/lib2]

单元以及在激进时序优化阶段插入的变化。除了缓冲器之外，还会忽略时钟和复位线以及常量，以避免在分解过程中引入噪声。

k和表格中的 $\rho_s$ 参数提供了用于确定k‐最近邻以及输入到匹配算法的最终分配矩阵稀疏性的值。#FB 显示了原始电路中不同功能模块的数量。

以类似的方式，我们获得了参考电路的标签（通过读取在综合参考HDL期间从HDL模块名称保留下来的连线前缀），事实上，在我们的实验中，我们也知道测试电路中的节点实际属于哪个功能模块，并利用该信息来检查最终匹配的准确性。关于测试网表的这一信息仅用于评估我们工具的最终匹配结果，而不会在算法的其他任何地方使用。[M1]和[M2]分别提供了清理阶段之前的匹配结果和清理阶段之后的匹配结果。

$\rho_s$ 参数表示我们决定在代价矩阵的每一行和每一列中保留的条目数量。它对最终匹配结果没有显著影响，但有助于使二分图变得稀疏，从而减少大型电路的运行时间。然而，在为某个设计选择参数时，应谨慎确保保留足够的条目，以便正确/最优分配对在代价矩阵中保持激活状态。一个好的取值方法是将 $\rho_s$ 设置为接近参考电路中平均簇大小的数值，这通常能给出一个良好的估计。

表5. 为使亲和矩阵对称而添加的新元素百分比

电路	TA/lib1	TA/lib2	工具B/lib2
	参考	测试（时间）	测试（面积）
新元素（%）	新元素（%）	新元素（%）	新元素（%）
Wishbone内存控制器	0.21	0.21	0.21
MIPS32处理器	0.18	0.18	0.17
PID控制器	0.17	0.18	0.18
里德‐所罗门编码器	0.10	0.10	0.10
8051微控制器	0.20	0.19	0.22
浮点运算单元	0.13	0.13	0.13
AES密码	0.18	0.17	0.17
OpenSpart T1处理器	0.23	0.28	0.24

为了降低初始全矩阵的密度而不影响匹配算法，但可以根据时间或内存限制，或需要更多样本的特定设计来调整参数。

选择k会改变相似性矩阵，从而影响特征分解。该参数应选择得足够大以去除噪声，但又足够小以保持簇之间的分离。一种常用的基本方法是设置 $k= \sqrt{n}$，其中 $n$ 是设计中节点的数量。在我们的实验中，并未观察到k对匹配结果有显著影响，因此未单独绘制相关图表。我们相信其原因是大多数电路中每个功能模块内的门电路之间具有足够多的互连。（除了最终清理阶段，在该阶段我们检查节点的k近邻，由于所用方法在图中计算最短路径的性质，k对基于I/O的特征没有影响。）如前所述，在完成k近邻计算后，矩阵会通过新增元素进行编辑以实现对称性，从而实现无向边构造。表5显示了在k近邻计算后添加到相似性矩阵中的新元素的百分比。此处读者应注意，这些元素是以特定权重添加到相似性矩阵中的。较高的k值或大量新节点并不一定意味着图中节点之间的连接更强。如前所述，边的相似性值用于创建这些连接，而彼此距离较远的节点仅以较弱的方式连接。

确定特征向量数量对于嵌入质量至关重要。我们使用特征间隙启发式方法[26]，其中根据相应特征值图中最大的间隔，将具有非零特征值的特征向量进行划分。例如，如果特征值 $\lambda_d$ 和 $\lambda_{d+1}$ 之间存在显著间隔，则取前d个特征向量作为分解的主导特征，移除对应零特征值的特征向量，并忽略其余部分。（表1–4 中的 $d_1$ 和 $d_2$ 值显示的是在移除零特征值向量之前的初始d值。嵌入与对齐计算是在移除这些向量之后进行的。）初始嵌入维度d通常对应于参考设计中聚类数量附近的值。因此，最好以略大于功能模块数量的值开始分解，然后检查特征值图，找出其后跟随相对较大 $\lambda_{d+1}$ 间隔的一组最小的d个特征值。然而，d 不一定必须等于功能模块数量。较少的特征向量仍可将空间划分为多个分区，或者特征向量可能为设计的功能簇提供与#FB值不同的粒度。图8展示了三个基准测试的示例特征值图，其中测试电路与参考电路的间隔均清晰可见。

总体而言，基于特征分解和基于I/O的特征都被证明是有效的嵌入工具，可用于寻找两个电路之间的对应关系，并且在识别高层级模块时可达到高达99%的准确性。清理阶段还有助于纠正这两种技术的不匹配问题，从而提升匹配结果。即使在电路之间存在较大尺寸差异的情况下（例如1–4中浮点运算单元 基准测试所示，该设计可进行高强度的性能优化而不会出现时序违规，并且面积显著增加），我们仍获得了非常高的覆盖率，尽管参考电路的规模几乎是另一个电路的两倍。通常情况下，在初始匹配结果中，由于特征数量较多（等于每个基准测试中的I/O端口数量），基于I/O的特征相比特征特征提供了更好的结果。然而，在Wishbone conmax IP基准测试中，由于I/O向量中特征过多，表现出不同的行为。尽管3和4中的电路图受影响不大，但我们观察到，当电路图更大时，大量的I/O端口可能会引入一些噪声，如1和2所示。当同时使用基于I/O和基于特征分解的特征进行匹配时，特征向量有助于调节这种噪声，从[M2]列的表格1和2可以看出，在组合情况下获得的结果高于单独使用I/O或特征特征的情况。

我们观察到的另一个有趣结果是，sparc基准测试在表1和2中两种情况下的I/O‐based匹配准确率之间的差异。尽管表3和4中相同基准测试的电路具有很高的匹配百分比（参见[M2]节中的I/O

表6. 设计基准的运行时间统计（秒）

电路	时间 TA/lib2 输入/输出特征 E‐特征 输入/输出与E 输	面积 TA/lib2 入/输出特征 E‐特征 输入/输出与E 输入	时间 TB/lib2 /输出特征 E‐特征 输入/输出与E 输入/输	面积 工具B/lib2 出特征 E‐特征 输入/输出与E
Wishbone内存控制器	42 30 46 328 768 752 5 5 7 10 4 11 872 1154 1347 4118 477 4006 2405 4750 4404 83 19 92 13387 129183 136771	41 30 48 384 1446 1396 5 5 7 9 4 10 962 1163 1371 4043 409 3993 2454 5678 5459 80 19 88 26807 83534 78785	36 39 51 430 1825 1864 7 7 8 9 4 10 338 714 694 493 1557 4068 2465 6273 6261 139 64 144 80567 92961 132576	36 43 55 416 1242 1375 7 6 8 10 5 10 394 720 700 3991 1157 3889 2915 5109 5312 131 96 141 70646 94910 115032
MIPS32处理器
PID控制器
里德‐所罗门编码器
8051微控制器
Wishbone conmax IP
浮点运算单元
AES密码
OpenSparc T1处理器

特征 列，见表 3和4），表 1和2显示，当测试图明显大于参考图时，即使在对未标记节点进行清理/校正阶段之后，基于输入/输出的匹配结果也会发生显著变化（参见对应的 [M2] 列）。图的尺寸差异是影响大型电路中基于输入/输出匹配的一个重要因素。如前一节所述，这也是为什么对于一个图相对另一个图较大的设计，我们建议在清理阶段首先对已标记节点进行一轮校正，然后再继续对未标记节点进行后续迭代（∼5k 节点差距是做出此决策的良好阈值）。结果表明，与基于输入/输出的特征提取相比，特征分解对尺寸差异更具鲁棒性。我们认为，基于特征分解的特征在 [M1]和 [M2]结果之间的显著改进，是由于测试电路中已标记节点初始稀疏性所致——这种稀疏性由较大的尺寸差异引起。

总之，对于I/O特征数量并非极大的常见情况（根据我们的结果，如果I/O端口数量与电路规模的比值小于10%），并且在移除两个电路中的缓冲器后，测试电路的规模与参考设计大致相当时，我们建议仅使用I/O特征，以避免其他特征集干扰精度；而当I/O端口数量异常大时，则建议结合使用I/O特征和基于特征分解的特征。对于电路图之间尺寸差异较大的情况——这通常意味着为了满足给定工艺库的约束，电路使用了更多的硬件和面积资源，从而导致相较于另一电路图更大的面积开销——我们再次推荐结合使用这两类特征，因为对于规模差距较大的设计，I/O端口数量可能不足以提供精确的嵌入，而特征特征更为可靠（∼104 gap通常是判断此情况的一个合理阈值）。

我们认为，基于特征分解的技术是一种强大的工具，它与输入/输出特征相结合，能够增强我们技术的鲁棒性，并且仅使用相对较少的特征即可提供准确的嵌入坐标。由于结果可能因设计而异，且两种方法在清理阶段后均能提供足够高的准确性，使得人工分析员可以通过手动分析校正边界，因此我们的建议是根据输入/输出端口与电路规模的比例以及图规模的差异（如上所述）在这两种技术之间做出选择。

表 6显示了我们实验的运行时统计。特征的数量以及特征区分分配的速度会对运行时间产生很大影响，但通过比较表1–4中的电路规模可以看出，被比较电路的规模和稀疏性值总体上是影响运行时间的两个主要因素。较小的稀疏性值可以降低速度。这可能会在准确性上产生轻微的权衡，但该方法总体上相当稳健，准确性不会发生剧烈变化。当

当$\rho_s$参数超过某个值时，即使将其设置为更大的数值，分配结果也不会发生显著变化。因此，在我们的实验中，我们倾向于选择接近这种饱和点的数值来设定 $\rho_s$的值。如前所述，参考电路中的平均簇大小可以为此提供一个良好的估计。该代码可用于工业应用，并通过更优化的代码实现来提升性能，同时借助更快的处理器和更多并行化手段提高速度（代价矩阵计算可采用完全并行化）。我们已尽最大努力用于学术研究演示，针对具有高复杂性特征的决策问题获得了合理的运行时间。

我们希望提醒读者注意的另一个问题是我们在最后阶段所采用的分配算法。在本研究中，我们提出了一个用于电路图几何嵌入的框架，提供了两种鲁棒特征提取方法，并通过使用高效的线性分配求解器展示了我们工作的有效性。然而，对于可能利用我们研究成果的未来工作而言，值得指出的是，根据所需的效率‐速度权衡，最后一步可以替换为其他匹配算法。例如，针对稀疏或稠密矩阵的改进的匈牙利算法、并行化分配算法或基于整数线性规划（ILP）公式的方法都是一些可行的建议，且均值得进一步探索。我们非常期待看到此类扩展工作的成果。线性分配问题存在大量解决方案，我们建议 [8]有兴趣的读者参考对这些算法的全面研究。

我们再次强调，我们的工具所针对的覆盖率并非精细匹配，例如移位寄存器或计数器识别。它是在块级进行的，并利用参考设计信息推断这些模块在不可信测试电路中的位置，而我们所追求的匹配精细程度（或粗略程度）可通过查看表格中的#FB（功能模块数量） 参数来了解。该参数与电路规模共同决定了每个设计的高层级覆盖率。我们的工具解决了在大量逻辑门中寻找模块边界的问题，用于不可信测试电路。表1–4中M列的最终匹配结果表明了我们方法的有效性，即仅使用相对较少的特征即可实现超过90%的准确率来识别此类高层级模块。

4 结论

随着全球化且不可信的集成电路设计与制造流程的发展，逆向工程在检测恶意更改方面正变得越来越重要。本文研究了用于逆向工程的功能划分问题。我们提出了一种利用几何嵌入计算参考设计和测试设计节点之间对应关系的方法。该方法有助于将测试设计划分为与参考设计相对应的高层级模块。这是实现最终目标的关键步骤，即检查每个划分模块的功能，以确保不存在恶意更改。所识别出的高层级模块可进一步分析，以验证其功能或发现恶意更改。实验表明，该划分方法在来自OpenCores的八个电路以及OpenSparcT1处理器上的实际有效性。