排序算法

冒泡排序

先来个最简单的，一般都是最先接触的算法：冒泡排序

冒泡排序的思路也很简单，用升序排序来看，就是依次比较相邻的数字，如果前一个数字大于后面的那个，就交换两数（即把大数后移），假设数组长度为size，
第一轮比较完毕时，就把最大数移动到了 下标size-1 处

第二轮就在下标0到size-2中找到第二大的数字，并移动到下标size-2处，

循环往复，循环size-1 或 size轮即可完成排序

代码也很简单：

void BubbleSort(vector<int>& nums)
{
	int size = nums.size();
	//第一个for决定循环层数
	for (int i = size-1;i>0;--i)
	{//第二个for决定每一层里的循环次数
		for (int j = 0;j<i;++j)
		{
			if (nums[j] > nums[j + 1]) swap(nums[j], nums[j+1]);
		}
	}
}

快速排序

接下来介绍一下冒泡排序的升级版：快速排序
为什么说快速排序时冒泡排序的升级版，因为快速排序也是通过数组元素之间的比较交换来达成排序的

快速排序就是在一定的区间内找一个数字key，然后把整个区间分类，以升序为例，比key小的就放到左边，比key大的就放到key的右边，最后key就会被放到正确的位置上，然后获取key位置的下标，这此时整个区间就被key分成了两个部分
begin 到 key-1 和 key+1 到 end
然后对这两个区间继续进行上面的步骤，直到把整个数组的所有数字都放到正确的位置上

于是我们直到，分割归位的程序时最重要的，
我们叫它partition （分割）

代码：

int partition(vector<int>&nums,int L, int R)
{
	int key = nums[L];//我们每次都取区间的第一个数作为key进行归位
	while(L < R)
	{//这里得注意，如果我们用nums[L]做基准，下面的while就得先对R进行判断，反之亦然，不然就会出错
		while(L < R && nums[R] >= key) --R;//满足大于key的条件就不用管了，找到不满足的再说
		swap(nums[L], nums[R]);//找到不满足的，进行交换
		while(L < R && nums[L] <= key) ++L;
		swap(nums[L], nums[R]);
	}
	return L;//执行完上面的程序之后，L == R不管返回那个都行，都是key的最终下标
}

这里我们每次都是用的nums[L]的值用作key，其实有更高效率的做法，那就是随机值

用rand在区间内随机一个下标keyidx，交换nums[L] 与 nums[keyidx]，当然与nums[R]交换也是一样的，记得改while语句的顺序就好了

随机选择key值代码：

int keyidx = (rand()%(R-L+1))+L;//保证在L到R之间随机
swap(nums[L], nums[keyidx]);
key = nums[L];

当然，也可以提前在主函数里设置好时间随机种子

srand(time(NULL));

最重要的分割归位程序完成了其他的就简单了

分割程序语句决定好一个位置，并且把数组分成两部分了，那我们就继续对着两部分递归的进行分割归位，然后一路递归下去…直到数组中所有区间的上半部分被排序完，然后对区间的下班部分进行排序…（整个顺序可以随意改变，先上还是先下无所谓的）
代码：

void QSort(vector<int>&nums,int L, int R)
{
	if(L >= R)return;
	else
	{
		int idx = partition(nums, L, R);//切割排序获得第一个主元的下标
		QSort(nums, L, idx-1);//对下子区间进行分割归位
		QSort(nums, idx+1, R);//同理
	}
}

到这一步，快速排序已经完成了，我们只需要再封装一下就可以了
代码：

class Solution {
    int pratition(vector<int>& nums,int L, int R)
    {
        int keyidx = (rand()%(R-L+1))+L;
        swap(nums[keyidx],nums[L]);
        int key = nums[L];
        while(L < R)
        {
            while(L < R && nums[R] >= key) --R;
            swap(nums[L], nums[R]);  
            while(L < R && nums[L] <= key) ++L;
            swap(nums[L], nums[R]);          
        }
        return L;
    }
    void QSort(vector<int>& nums,int L, int R)
    {
    	if(L >= R) return;
        else
        {
            int idx = pratition(nums, L, R);
            QSort(nums, L, idx-1);
            QSort(nums, idx+1, R);
        }
    }
public:
    vector<int> QuickSort(vector<int>& nums) {
    	srand(time(NULL));
        int L = 0, R = nums.size()-1;
        QSort(nums,L,R);
        return nums;
    }
};

其实快速排序也意外的简单，写出partition程序就差不多了

---

归并排序

归并排序的思路如下



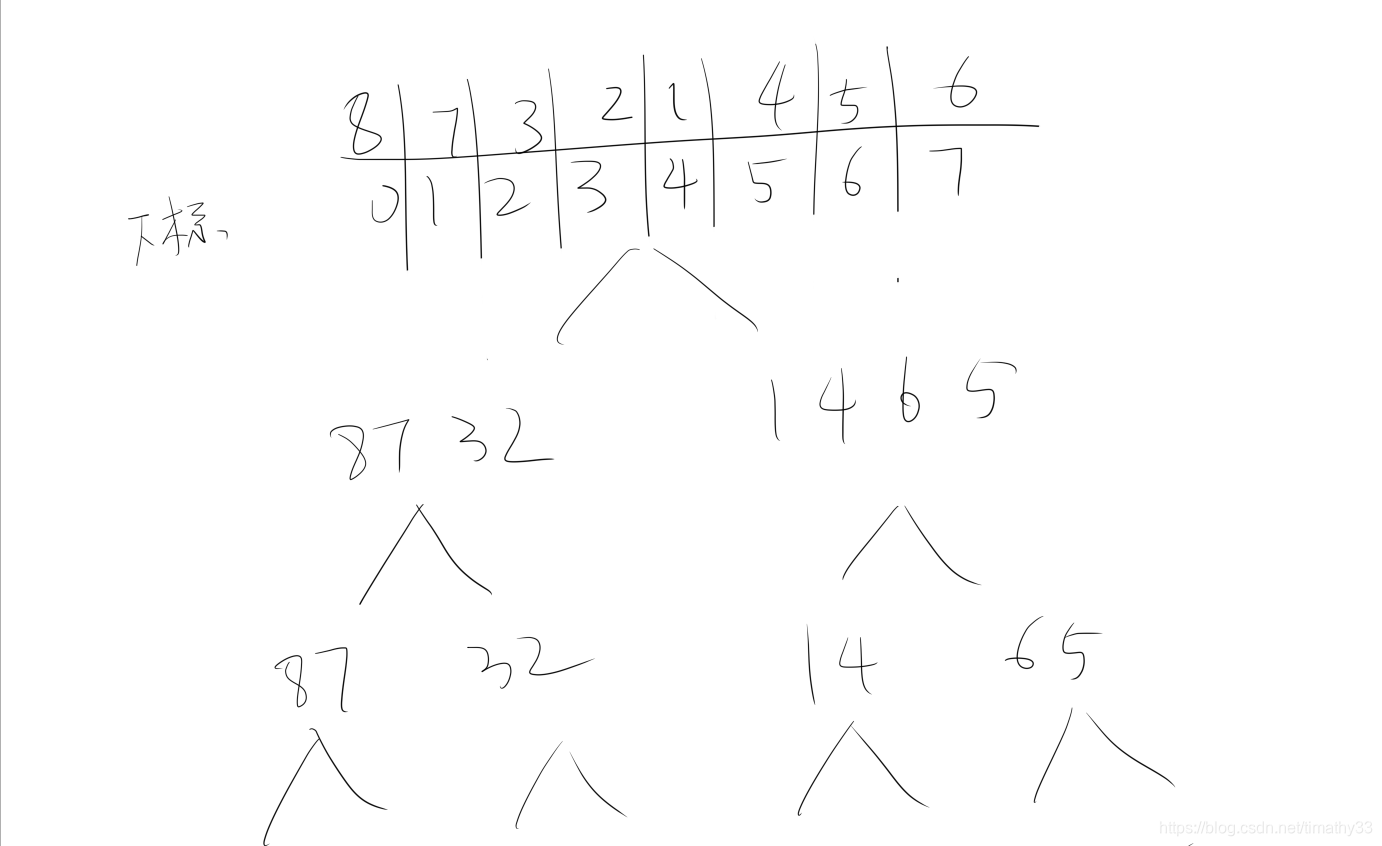
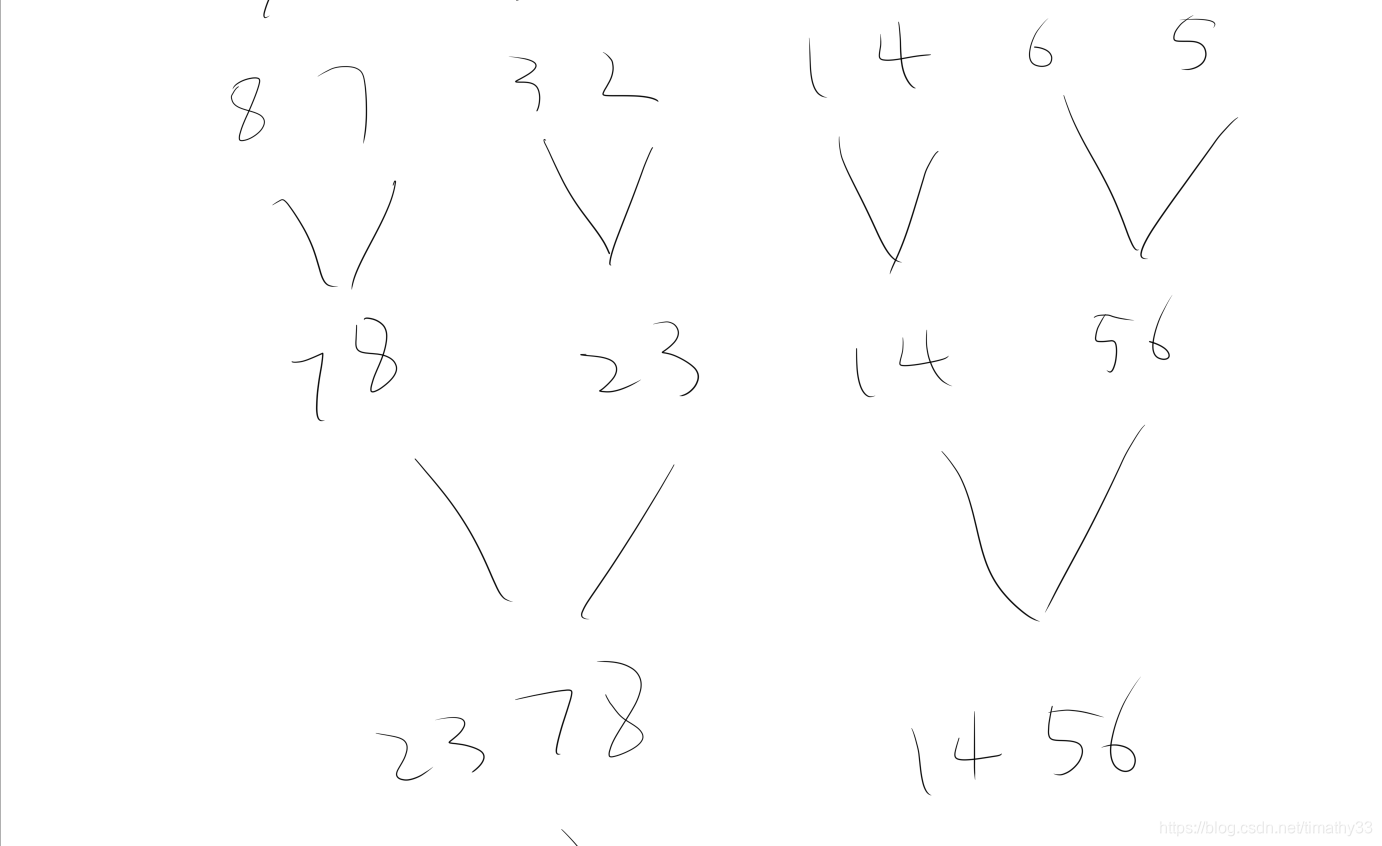
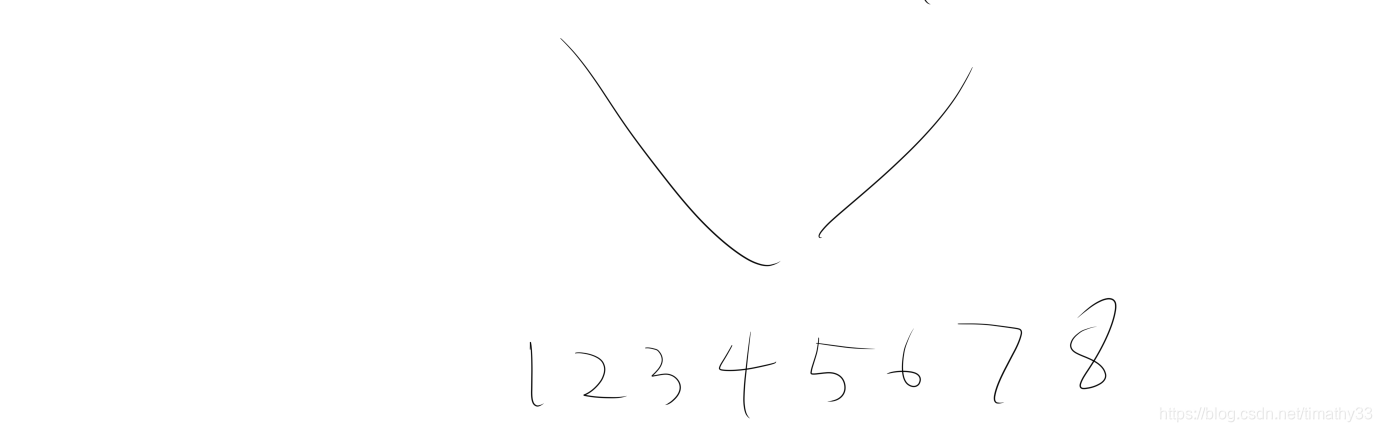
虽然思路是这样，但是意外程序执行的顺序和递归的性质，代码再执行的时候总是先排序某一边（看代码怎么写，可左可右）

代码：
主要程序：

void MSort(vector<int>&nums,int L, int R)
{
	if(L >= R)return ;
	else
	{
		int mid = L+((R-L)>>1);
		MSort(nums,L,mid);//先左
		MSort(nums,mid+1,R);//后右
		Merge(nums,L,mid,R);//合并
	}
}

合并的程序：

void Merge(vector<int>& nums,int L, int mid, int R)
{
	vector<int>temp(R-L+1);//临时数组
	int i = L, j = mid+1, idx = 0;
	while(i <= mid || j <= R)//合并而已，怎么写都行，下面会有另一种方法
	{
		int num1 = i <= mid?nums[i]:INT_MAX;
		int num2 = j <= R?nums[j]:INT_MAX;
		if(num1 <= num2)
		{
			temp[idx++] = num1;
			++i;
		}
		else
		{
			temp[idx++] = num2;
			++j;
		}
	}
	//合并完了就覆盖回原数组
	for(int i = 0;i<R-L+1;++i)  nums[L+i] = temp[i];
}

合并的另一种写法，用哪个都没差，不过这个更加简洁，也没有其他临时变量

while(i <= mid && j <= R)
{
	temp[idx++] = nums[i] <= nums[j]?nums[i++] : nums[j++];
}
while(i <= mid) temp[idx++] = nums[i++];
while(j <= R)	temp[idx++] = nums[j++];

封装：

class Solution {
	void Merge(vector<int>&nums, int L, int mid, int R)
	{
		vector<int>temp(R-L+1);
		int i = L, j = mid+1, idx = 0;
		while(i<=mid && j<=R) temp[idx++] = nums[i]<= nums[j]?nums[i++]:nums[j++];
		while(i<=mid) temp[idx++] = nums[i++];
		while(j<=R) temp[idx++] = nums[j++];
		for(int i = 0;i<R-L+1;++i)	nums[L+i] = temp[i];
	}
	
	void MSort(vector<int>&nums, int L, int R)
	{
		if(L >= R) return;
		else
		{
			int mid = L+((R-L)>>1);
			MSort(nums,L,mid);
			MSort(nums,mid+1,R);
			Merge(nums,L,mid,R);
		}
	}
public:	
	void MergeSort(vector<int>&nums)
	{
		int L = 0, R = nums.size()-1;
		MSort(nums,L,R);
	}
};

---