剑指 Offer 38. 字符串的排列
输入一个字符串,打印出该字符串中字符的所有排列。
你可以以任意顺序返回这个字符串数组,但里面不能有重复元素。
示例:
输入:s = “abc”
输出:[“abc”,“acb”,“bac”,“bca”,“cab”,“cba”]
来源:力扣(LeetCode)
思路
全排列,考虑使用回溯算法,但我刚接触回溯算法,能看懂,但不是特别熟悉,以下都是自己的理解,果有错误的地方,请指出!
由下图可以看出,全排列的本质可以看成记录下面这颗树的所有路径,用递归的方法就能很好的达成目的,题目要求不能重复,那我们用set自动去重就好了
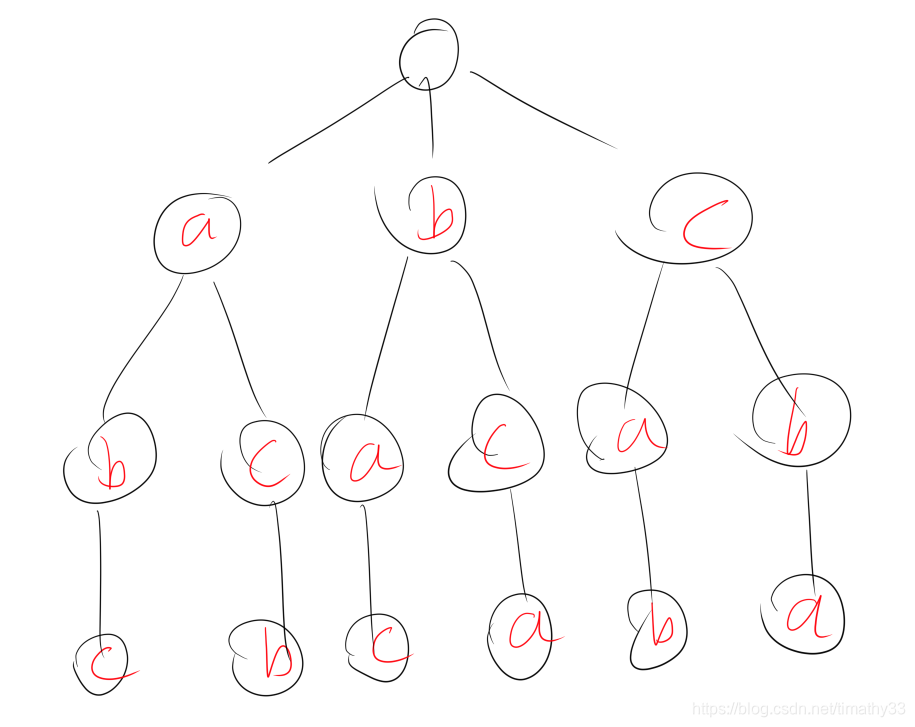
我们用一个for循环来选择不同的路径起点(a , b , c)
用一个string来存储每一个完整的路径,即结果,我们叫他cur吧
在走过的地方做标记,好让后面递归时里的for循环能跳过已经走过的结点
然后时最重要的递归基的设置,当我们走完一条路径的时候,即cur的长度为3的时候(这里假设输入的是“abc”长度为3),这时候cur就存储了一个结果,就该返回,并把cur的结果存进set里面
存放了一个结果以后,我们还得撤销选择,即让曾经的标记失效,好让后续的遍历能得到正确的结果,这个时候,我们的for就用发挥了作用,让路径从b开始,然后后面的就重复以上步骤啦
class Solution {
public:
unordered_set<string> mset;
void dfs(string&s , string&cur , vector<bool>&flag)//
{
if(cur.size() == s.size()) //递归基
{
mset.insert(cur);//把结果放入set
return ;
}
for(int i = 0;i < s.size();i++)
{
if(flag[i]) continue;//跳过已经标记的元素
flag[i] = true;//标记
cur += s[i];//记录路径
dfs(s,cur,flag);//往下搜索
flag[i] = false;//撤销标记
cur.pop_back();//清空cur
}
}
vector<string> permutation(string s) {
vector<string> res;
string cur = "";
vector<bool> flag (s.size() , false);//标记用数组
dfs(s,cur,flag);
for(auto& buf : mset)//遍历set并把结果放入res中
{
res.emplace_back(buf);
}
return res;
}
};
更新:
曾经用的set去重,实属是不够看,效率太低了,随着对回溯理解的加深,现在回想起来,可以用排序+剪枝的方法去重
先说说剪枝的原理,先把原字符串排序,然后判断当前字符是不是和上一个字符相等,然后再判断上一个字符是否刚被撤销选择,因为再同一个选择列表里进入下一个选择的时候,肯定刚刚撤销上一个选择,我们就这样判断
flag[i] == false[i-1]&&s[i] == s[i-1];
然后别忘了全排列是从0开始的,我们要判断[i-1]的话,i必须大于0,不然数组就越界了,会出错
最后就是这样
i>0 && flag[i] == false[i-1] && s[i] == s[i-1];
i>0记得写前面,因为&&的短路特性,一旦i>0为false,那么程序就不会执行后面的判断,也就不会越界出错
代码:(这模板还能直接套在其他排列题上)比如:47. 全排列 II
class Solution {
public:
vector<string>res;
void dfs(string&s , string&cur , vector<bool>&flag)
{
if(cur.size() == s.size())
{
res.emplace_back(cur);
return ;
}
for(int i = 0;i< s.size();i++)
{
if(flag[i] || (i>0 && s[i] == s[i-1]&&!flag[i-1])) continue;//剪枝
cur += s[i];
flag[i] = true;
dfs(s,cur,flag);
flag[i] = false;
cur.pop_back();
}
}
vector<string> permutation(string s) {
vector<bool>flag(s.size(),false);
string cur = "";
sort(s.begin(),s.end());//排序
dfs(s,cur,flag);
return res;
}
};
46. 全排列
这题是数字的全排列,其实和上一题没啥区别,也是用一个flag数组来标记,然后做出选择,递归,撤销选择
class Solution {
vector<vector<int>> res;
public:
void dfs(vector<int>& nums,vector<int>& temp , vector<bool>&flag)
{
if(temp.size() == nums.size())
{
res.emplace_back(temp);
return ;
}
for(int i = 0;i<nums.size();i++)
{
if(flag[i]) continue;
flag[i] = true;
temp.emplace_back(nums[i]);
dfs(nums,temp,flag);
flag[i] = false;
temp.pop_back();
}
}
vector<vector<int>> permute(vector<int>& nums) {
vector<bool>flag(nums.size(),false);
vector<int>temp;
dfs(nums,temp,flag);
return res;
}
};
最近和回溯杠上了,必须玩懂回溯算法,今天做了一题,感觉理解又深了一点
39. 组合总和
给定一个无重复元素的数组 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的数字可以无限制重复被选取。
说明:
所有数字(包括 target)都是正整数。
解集不能包含重复的组合。
示例 1:
输入:candidates = [2,3,6,7], target = 7,
所求解集为:
[
[7],
[2,2,3]
]
来源:力扣(LeetCode)
这题简单又经典
求组合,还是一样,抛弃前面的数字,for循环从idx开始,而传入idx时不用+1,表示可以重复用当前数字,
最朴素的写法如下:(这还是我第一次自己写出来)
res.clear();buf.clear();sum = 0;
这几句对于题目没任何帮助,只是初始化要使用的数据而已,以防多次使用时得到得数据不一样,其实可以把这几个数据写进方法里,这样在调用完方法后系统会自动回收、
但是这样调用回溯得时候会很麻烦;
class Solution {
vector<vector<int>>res;
vector<int>buf;
int sum;
void backtrack(vector<int>& candidates,int idx,int target)
{
if(sum > target) return ;
if(sum==target)//只有==target时才填入结果数组
{
res.emplace_back(buf);
return ;
}
for(int i = idx;i<candidates.size();++i)
{
sum += candidates[i];//做出选择
buf.emplace_back(candidates[i]);//做出选择
backtrack(candidates, i, target);
sum -= candidates[i];//撤销选择
buf.pop_back();//撤销选择
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
res.clear();buf.clear();sum = 0;//初始化数据
//sort(candidates.begin(),candidates.end());
backtrack(candidates, 0, target);
return res;
}
};
效率一般般,还行吧
要提高效率,就必须减少递归的深度和次数,也就是减少无谓的递归,我们原来的递归是做出选择之后,所以我们得在递归前做出判断,看看下一次递归是不是没必要的,也就是所谓得 剪枝
想想我们怎么结束无用递归的,是在进入下一层递归之后,判断sum是否 > target,这时已经进入了走过无用的递归了,所以我们可以在进入递归之前就判断 sum是否 > target;这就是(剪枝)了,但是要这样剪枝,就必须要先对目标排序
class Solution {
vector<vector<int>>res;
vector<int>buf;
int sum;
void backtrack(vector<int>& candidates,int idx,int target)
{
//if(sum > target) return ;
if(sum==target)
{
res.emplace_back(buf);
return ;
}
for(int i = idx;i<candidates.size() /*&& sum+candidates[i]<=target*/;++i)
{
if(sum+candidates[i]>target)return;//也可以改成在上面的for里面判断
sum += candidates[i];
buf.emplace_back(candidates[i]);
backtrack(candidates, i, target);
sum -= candidates[i];
buf.pop_back();
}
}
public:
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
res.clear();buf.clear();sum = 0;
sort(candidates.begin(),candidates.end());//
backtrack(candidates, 0, target);
return res;
}
};
22. 括号生成
数字 n 代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。
示例 1:
输入:n = 3
输出:["((()))","(()())","(())()","()(())","()()()"]
来源:力扣(LeetCode)
思路:
如果要使括号能有效,那右括号就不能随便插,必须在左括号数量大于右括号数量的情况下插入,不然单插一个右括号不可能有效的
右括号的插入规则决定好了,接下来决定左括号的插入规则,左括号除了数量限制以外,没有其他规则
代码:
class Solution {
void dfs(vector<string>&s,int n,string& temp,int ln,int rn)
{
if(temp.size()== n+n)
{
s.push_back(temp);
return ;
}
if(ln < n)
{
temp.push_back('(');
dfs(s,n,temp,ln+1,rn);
temp.pop_back();
}
if(rn < ln)
{
temp.push_back(')');
dfs(s,n,temp,ln,rn+1);
temp.pop_back();
}
}
public:
vector<string> generateParenthesis(int n) {
string temp;
vector<string> res;
dfs(res,n,temp,0,0);
return res;
}
};
78. 子集
给你一个整数数组 nums ,数组中的元素 互不相同 。返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。你可以按 任意顺序 返回解集。
示例 1:
输入:nums = [1,2,3]
输出:[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]
来源:力扣(LeetCode)
自己问题和什么排列不一样,比如给定的数组是{ 1, 2, 3}
{ 1 }也是子集,也就是说,
每次递归都需要把路径填入结果数组
排列得等到路径长度达到最大时才填入
然后,组合也不需要考虑顺序,所以当从1作为起点的所有结果都被我们填入结果数组之后
(也就是第一层dfs程序里的for循环完成了一次,进入第二次循环的时候)
我们就得抛弃1了,让后续的递归循环从2开始就行了,所以我们不需要前面全排列的flag数组了,因为我们后续的循环都抛弃了前面的数字
全排列的话,就算路径从2开始,也不能放弃前面的1;
为此,我们需要用一个参数,控制for的循环起点
代码:
class Solution {
vector<vector<int>>res;
vector<int>buf;
void dfs(vector<int>& nums, int idx)//idx就是用来控制循环起点的
{
res.emplace_back(buf);//不论情况都得填入结果数组
for(int i = idx;i<nums.size();++i)//这里记得i的初值的赋值为idx哦,不然idx就没意义了
{
buf.emplace_back(nums[i]);//选择路径
dfs(nums,i+1);
buf.pop_back();//撤销选择
}
}
public:
vector<vector<int>> subsets(vector<int>& nums) {
dfs(nums,0);
return res;
}
};
90. 子集 II
给你一个整数数组 nums ,其中可能包含重复元素,请你返回该数组所有可能的子集(幂集)。
解集 不能 包含重复的子集。返回的解集中,子集可以按 任意顺序 排列
来源:力扣(LeetCode)
思路:
代码基本上和上一题一模一样,只多了一句,减去重复的选择列表(剪枝)
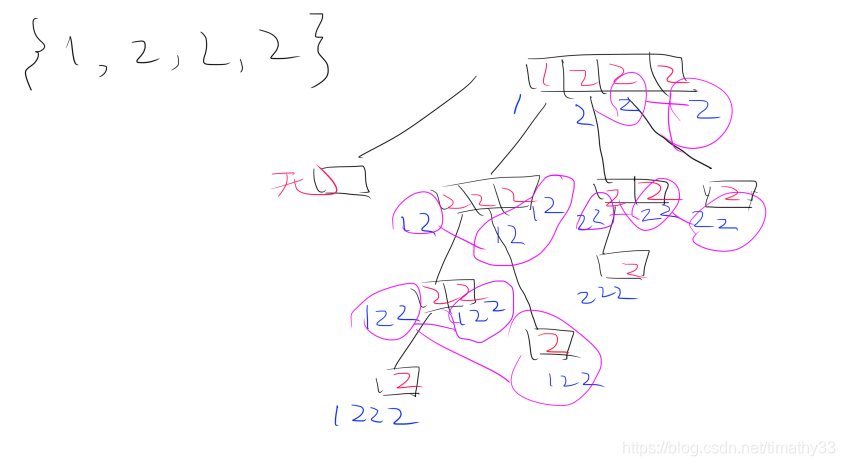
由上图可见,红色的是选择列表,蓝色的是被填入结果数组的buf,紫色的是重复的buf,可以发现,重复的紫色都出现在重复的选择列表之下,因此只要我们跳过重复的选择列表就行了
于是有以下代码:
if ( nums[i] == nums[i-1] ) continue;
但是要注意, 就算现选择列表重复了,我们也得选一个,第一个选择是不能抛弃的,也就是说在一次递归里,for的第一次循环不能跳过
于是将上面代码修改为
if ( i > idx && nums[i] == nums[i-1] ) continue;
为什么要>idx 呢?因为idx是我们给for循环的初值,必须大于初值且选择列表重复了才跳过
于是在回溯搜索里的for循环里加上这一句就ok了
void dfs(vector<int>& nums, int idx)//idx就是用来控制循环起点的
{
res.emplace_back(buf);//不论情况都得填入结果数组
for(int i = idx;i<nums.size();++i)//这里记得i的初值的赋值为idx哦,不然idx就没意义了
{
if ( i > idx && nums[i] == nums[i-1] ) continue;//剪枝
buf.emplace_back(nums[i]);//选择路径
dfs(nums,i+1);
buf.pop_back();//撤销选择
}
}
17. 电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。答案可以按 任意顺序 返回。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
来源:力扣(LeetCode)

示例 1:
输入:digits = “23”
输出:[“ad”,“ae”,“af”,“bd”,“be”,“bf”,“cd”,“ce”,“cf”]
用哈希表来存储(字符串),每个数字对应的字母
然后就是一样差不多的套路了,递归进入下一层选择,for进行当层选择列表的选择,然后别忘了选择和撤销选择,还有递归基,这里我把哈希表,缓冲数组,等等全部放入了函数里,也可以直接在类中定义,不过直接在类中定义的话比较方便
class Solution {
void backtrack(string&s,int idx,unordered_map<char,string>&map,vector<string>&res,string &buf)
{
if(buf.size() == s.size())//长度够了就填入结果数组
{
res.push_back(buf);
return ;
}
const string& temp = map[s[idx]];//获得选择列表,就是手机当前数字的字符串
for(char ch : temp)
{
buf.push_back(ch);
backtrack(s, idx+1,map,res,buf);
buf.pop_back();
}
}
public:
vector<string> letterCombinations(string digits) {
unordered_map<char,string>map =
{
{'2',"abc"},{'3',"def"},{'4',"ghi"},{'5',"jkl"},
{'6',"mno"},{'7',"pqrs"},{'8',"tuv"},{'9',"wxyz"}
};
vector<string>res;
string buf;
if(digits.empty())return {};
backtrack(digits,0,map,res,buf);
return res;
}
};
79. 单词搜索
给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
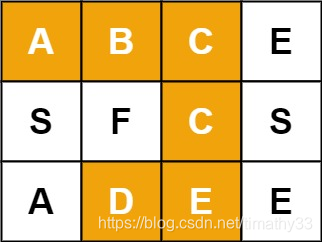
输入:board = [["A","B","C","E"],["S","F","C","S"],["A","D","E","E"]], word = "ABCCED"
输出:true
来源:力扣(LeetCode)
思路:
遍历搜索整个二位u数组,如果某个地方能作为单词的开头,就从那个地方开始进行搜索,上下左右都要搜,如果上下左右有一个等于单词的下一个字符,就再次对那个点进行递归搜索,当然时搜索下一个字符,
如果进行递归搜索的次数和单词的长度相等,就说明找到了,就这么简单
只要注意两点就行:
一:数组别越界
二:别重复使用同一个位置
像全排列一样用一个flag数组来标记是否被使用
代码:
class Solution {
bool res;
int length;
void backtrack( vector<vector<bool>>&flag,vector<vector<char>>& board,string& word,
int row,int col)
{
++length;//因为满足条件才递归,所以每次都+1
if(length == word.size())
{//如果长度达标就说明找到了,返回
res = true;
return ;
}
flag[row][col] = true;//标记
/*对上下左右进行判断,是否时下一个字符*/
//桑条件分别时 是否越界、是否是单词的下一个字符、是否被使用过
if(row>0 && board[row-1][col]==word[length]&&!flag[row-1][col])
backtrack(flag,board, word,row-1, col);
if(row<board.size()-1 && board[row+1][col]==word[length]&&!flag[row+1][col])
backtrack(flag,board, word,row+1, col);
if(col>0 && board[row][col-1]==word[length]&&!flag[row][col-1])
backtrack(flag,board, word,row, col-1);
if(col<board[0].size()-1 && board[row][col+1]==word[length]&&!flag[row][col+1])
backtrack(flag,board, word,row, col+1);
flag[row][col] = false;//撤销标记
--length;//撤销选择
}
public:
bool exist(vector<vector<char>>& board, string word) {
res = false;
int row = board.size(),col = board[0].size();
vector<vector<bool>>flag(row,vector<bool>(col,false));
for(int m = 0;m<row;++m)
{
for(int n = 0;n<col;++n)
{
if(board[m][n]==word[0])//两个for遍历二维数组
{
length = 0;
backtrack(flag,board,word,m,n);
if(res==true)
return true;
}
}
}
return false;
}
};
在剑指offer里也做了一下这题,但是会超时?怎么回事呢?明明在主站也是双90的
经过研究才发现,剑指offer那边用例重复性高,但数据量小,主站的重复性不高,但是数据量大
重复性高即需要剪枝,要破局也很简单,加一句即可
改一下递归基,把条件多加一个 || res
这样就很有效的剪枝了
if(length == word.size() || res==true)
照原来的代码,就算找够了长度,也还是会继续寻找,毕竟4个if可不是else的关系啊,假如从当前位置的左边除法找到了,但是就算找到了,其他三个方向if的寻找也不会停止,于是直接加上一个res在里面,一旦找到就不管了,别再找后续了
131. 分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
来源:力扣(LeetCode)
这一题其实就是普通的组合题啊!但是我没反应过来,没有理清分割的本质
所谓分割一个串,我们可以把它看成是求串的多个组合,只不过这些组合连起来刚好等于那个串而已
套个组合回溯的模板就行了,不过细节问题需要稍微改变一下
组合,排列,子集的模板见这里👉
需要改变的有一下几点:
递归基:
组合的模板的递归基是组合的长度,但是这一题不太一样,我们要求多个组合,且多个组合加起来必须等于原串,所以我们在遍历完一次原串后返回
for的跳过条件:
组合题要跳过一般是为了剪枝,去除无谓的重复答案和计算,这一题也很好理解,跳过不是回文串的情况嘛,因为题目只要回文串啊
从代码就能发现,改动真的很小啊,不过思路却不容易想,终究还是我太菜了
代码:
class Solution {
vector<vector<string>>res;
vector<string>buf;
bool IsPaliandrome(string& s)//判断是不是回文串的程序
{
int L = 0,R = s.size()-1;
while(L < R) if(s[L++] != s[R--])return false;
return true;
}
void dfs(const string &s,int idx)
{
if(idx>=s.size()) //一旦搜索完原串,就填入结果数组
{
res.push_back(buf);
return ;
}
for(int i = idx;i<s.size();++i)
{
string temp = s.substr(idx, i-idx+1);//获取当前组合
if(IsPaliandrome(temp)) buf.push_back(temp);//如果是回文串就填入缓冲数组
else continue;//否则跳过
dfs(s, i+1);
buf.pop_back();
}
}
public:
vector<vector<string>> partition(string s) {
res.clear();buf.clear();
dfs(s,0);
return res;
}
};
93. 复原 IP 地址
给定一个只包含数字的字符串,用以表示一个 IP 地址,返回所有可能从 s 获得的 有效 IP 地址 。你可以按任何顺序返回答案。
有效 IP 地址 正好由四个整数(每个整数位于 0 到 255 之间组成,且不能含有前导 0),整数之间用 ‘.’ 分隔。
例如:"0.1.2.201" 和 "192.168.1.1" 是 有效 IP 地址,
但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是无效 IP 地址。
来源:力扣(LeetCode)
这一题我想了半天回溯怎么剪枝,但是一直没做好,于是暂时放弃,先用暴力点的方法,幸亏ip地址长度有限,size超过12的可以直接放弃,因此暴力点的方法也能过
思路:
直接强行切割整个字符串,一旦切割完就返回,并在返回之前判断子串数量是否为4,且4段子串是否满足要求,只有当4段都满足要求才填入结果数组
代码:
class Solution {
vector<string>res;
vector<string>buf;
int ToNum(string&s)
{
int num = 0;
for(char&ch:s)
num = num*10+(ch-'0');
return num;
}
bool helper(string&s)
{//判断一个字符串是否满足要求
if (s.size() == 1) return true;
if(s.size()>1 && s[0]!='0' && ToNum(s)<=255) return true;
else return false;
}
void backtrack(string& s, int idx)
{//判断是否搜索完
if(idx >= s.size())
{//判断是否能填入结果数组
if(buf.size()==4&&helper(buf[0])&&helper(buf[1])&&helper(buf[2])&&helper(buf[3]))
{
string temp;
for(string& str : buf)
{//拼接
temp += str;
temp += '.';
}
res.emplace_back(temp);
}
return ;
}
for(int i = idx;i<s.size() && i<idx+3;++i)
{
int size = i-idx+1;
string ttemp = s.substr(idx, size);
buf.emplace_back(ttemp);
backtrack(s, i+1);
buf.pop_back();
}
}
public:
vector<string> restoreIpAddresses(string s) {
if(s.size()>12)return {};//长度超标直接return
backtrack(s, 0);
for(auto&str:res) str.pop_back();//去掉多余的一个点‘ . ’
return res;
}
};
剪枝的方法日后再说吧…
18. 四数之和
来个有意思的,三数之和用双指针还算舒服的,但是这个4数。写起来就很烦了,于是我就想。都这样了,不如用回溯试试,没想到真的能过,效率也还行吧
强行回溯不减枝的话,会在最后几个用例处超时,所以这题剪枝很重要,没剪好的后果就是这样
这里主要有两个最重要的剪枝:
if (i < nums.size() - 1 && sum + nums[i] + int(3 - path.size()) * nums[i + 1] > val) return;
if (sum + nums[i] + int(3 - path.size()) * nums[nums.size() - 1] < val)continue;
当然是我从大佬那学的,可以的话,直接看大佬的解释吧👉这里
(一)
因为数组已经排序过了,假设path的size为0,我们正要添加第一个数字进去,我们就可以检查一下,4 * nums[i]是否大于目标值,如果大于,那就没救了,后面的4个数之和,不管怎样,都会比4 * nums[i]大,return
同理,如果我们添加了一个数,正准备添加第二个数字,此时sum为path[0],我们看看nums[i]*3+sum是否大于目标值,大于就没救了直接return
同理,path的size为2,为3时也这样
(二)
第一个剪枝的判断是 :后续的值会不会过大,第二个剪枝就是判断会不会太小
具体思想差不多,只不过这里不是return,而是continue,因为数组递增,当前的位置不和书,不代表后续的都不合适
这里再说一下为什么int(3 - path.size())这一句要加一个int,因为size()返回的值是无符号数,用来运算的话,一旦遇上负数就会出错…坑了我10分钟来着
代码:
class Solution {
private:
vector<vector<int>>res;
vector<int>path;
int val;
void backtrack(vector<int>& nums, int idx, int sum)
{
if(sum == val && path.size() == 4 )
{
res.emplace_back(path);
return ;
}
for(int i = idx;i<nums.size();++i)
{
if(i>idx && nums[i] == nums[i-1])continue;//去重
if (i < nums.size() - 1 &&
sum + nums[i] + int(3 - path.size()) * nums[i + 1] > val) return;//剪枝
//剪枝
if (sum + nums[i] + int(3 - path.size()) * nums[nums.size() - 1] < val)continue;
path.emplace_back(nums[i]);
backtrack(nums, i+1,sum+nums[i]);
path.pop_back();
}
}
public:
vector<vector<int>> fourSum(vector<int>& nums, int target) {
val = target;
sort(nums.begin(),nums.end());
backtrack(nums,0,0);
return res;
}
};
51. N 皇后
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
来源:力扣(LeetCode)
对于我来说,这一题能放到困难难度,不是因为剪枝,而是因为二维的思想,怎么说呢,我一开始想的是用一个二维 bool数组来判断当前字符串的那个Q是不是能放,我想的是每次新建一个字符串,做了很久都没做出来,看了看大佬的题解,发现直接建立一个字符串数组,直接对这个数组进行操作,每次递归就进入下一个字符串,并且每次都从字符串的下标0开始往后遍历,判断有没有合适的位置
基本就是回溯模板套一下改一改的事,唉…
做选择就是将当前位置改成‘Q’, 回溯就是改回‘.’ 怎么样…很简单吧
说到底,数组里的不同字符串就是选择层数,字符串里的不同位置就是选择列表,还是我对回溯的理解不够透彻,才想不到,唉…
至于判断位置是否有效,也很简单,只需判断正上方,右上和左上即可,(因为我们是从上往下添加的,下面根本没有皇后)
用循环一个个判断,注意一下边界即可
代码:
class Solution {
vector<vector<string>>res;
int size;
void backtrack(vector<string>&buf,int row)
{
if(row == size)
{//如果已经找到最下方了,就说明皇后已经被放置完毕,可以填入结果数组
res.emplace_back(buf);
return ;
}
for(int col = 0;col<size;++col)
{
if(!check(buf,row,col))continue ;//如果是无效位置就跳过
buf[row][col] = 'Q';//做出选择
backtrack(buf,row+1);//
buf[row][col] = '.';
}
}
bool check(vector<string>&buf,int row, int col)
{//检查当前位置是否有效的函数
for(int i = 0;i<row;++i)
{//判断上方
if(buf[i][col] == 'Q')
return false;
}
for(int i = row-1, j = col-1;i>=0 && j>=0;--i,--j)
{//判断左上方
if(buf[i][j]=='Q')
return false;
}
for(int i = row-1, j = col+1;i>=0 && j<size;--i,++j)
{//判断右上方
if(buf[i][j]=='Q')
return false;
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
size = n;
vector<string>buf(size,string(size,'.'));//直接建立一个全是'.'的字符串数组
backtrack(buf,0);
return res;
}
};






















 543
543

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










