最大子数组-分治思想

原创已于 2025-07-26 21:03:50 修改 · 740 阅读

CC 4.0 BY-SA版权

文章标签：

于 2025-07-20 21:23:26 首次发布

假定我拿到了一个股市涨跌的数组vary [13,-3,-25,20,-3,-16,-23,18,20,-7,12,-5,-22,15,-4,7]。现在我想找出我该在什么时候买，什么时候卖才能赚的最多。（当然我可以手算，但是数组长度一旦多之后，那将是一件十分恐怖的事情😱）

让计算机帮我算呗😊

不动脑子就可以写出下面的算法

def max_subarray_sum(arr):
    max_sum = 0
    for i in range(len(arr)):  # i是子数组的起始位置
        for j in range(i, len(arr)):  # j是子数组的结束位置
            sum = 0
            for k in range(i, j+1):  # k是子数组的索引
                sum += arr[k]
            max_sum = max(max_sum, sum)
    return max_sum

但仔细分析一下，这个算法的时间复杂度是O(n^3)!一旦数组长度多了，这个算法就不尽人意了。

下面我们用分治的思想来考虑这个问题

如果您没接触过分治这个概念，不妨先了解一下分治的具体内容！

⭐⭐⭐⭐⭐

我们可以将一个数组划分为两个长度尽可能的数组。那么我们只需要分别求解这个长度更小的数组的最大子数组即可。这里就可以使用递归的思想了！很好，递归。

⚠

如果我们这样写出了代码

def find_max_subarray_divide_and_conquer(arr, low, high):
    # 递归出口
    if low == high:
        return low, high, arr[low]
    mid = (low + high) // 2
    # 左半部分
    left_low, left_high, left_sum = find_max_subarray_divide_and_conquer(arr, low, mid)
    # 右半部分
    right_low, right_high, right_sum = find_max_subarray_divide_and_conquer(arr, mid + 1, high)
    
    if left_sum >= right_sum:
        return left_low, left_high, left_sum
    else:
        return right_low, right_high, right_sum

那就大错特错了！

我们思考问题一定要考虑全面，想要考虑全面，就要先抓“全集”（这里我化用了数学中集合的术语）。在这问题中，最大子数组会出现在哪里，把这个“全集”考虑清楚了，就不会写出错误的代码了。

最大子数组可能出现的位置：

全部在左半边的数组
全部在右半边的数组
跨越中点的数组/左半边与右半边有交集的数组

没错，就是第三中情况我们刚刚给忽略掉了，以至于我们写出了错误代码。实际编程过程中类似的错误时常出现，但只要考虑好“全集”，这种考虑不周到的错误就可以杜绝了！

下面我们考虑寻找跨越中点的最大子数组

⭐

可以先从中点出发，找到左半边的最大子数组（含中点）,再从中点的下一位出发，找到右半边的最大子数组（当然可以从中点出发，但中点在计算最半边的时候已经被包含了，所以没有必要重复计算）。然后把左界和右界合并，就得到了跨越中点的最大子数组。

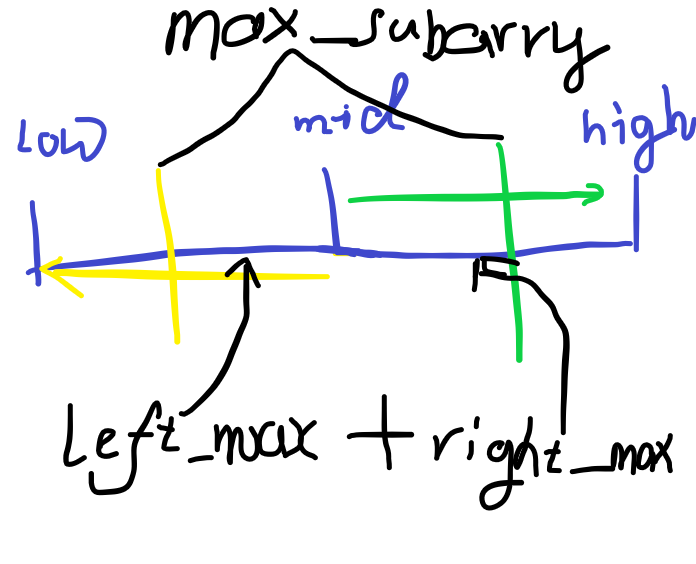
def FIND_MAX_CROSSING_SUBARRAY(A, low, mid, high):
    left_sum = -1000000000
    sum = 0
    # 左半边
    for i in range(mid, low-1, -1):
        sum += A[i]
        if sum > left_sum:
            left_sum = sum
            max_left = i
    # 右半边
    sum = 0
    right_sum = -1000000000
    for i in range(mid + 1, high + 1):
        sum += A[i]
        if sum > right_sum:
            right_sum = sum
            max_right = i
    
    return max_left, max_right, left_sum + right_sum

剩下的就简单了，比较“全集”中的三种情况的大小即可

def FIND_MAXIMUM_SUBARRAY(A, low, high):
    mid = (low + high) // 2
    if low == high:  # 递归出口，只有一个元素
        return low, high, A[low]
    # left 
    left_low, left_high, left_sum = FIND_MAXIMUM_SUBARRAY(A, low, mid)
    # right
    right_low, right_high, right_sum = FIND_MAXIMUM_SUBARRAY(A, mid + 1, high)
    # crossing
    crossing_low, crossing_high, crossing_sum = FIND_MAX_CROSSING_SUBARRAY(A, low, mid, high)

    if left_sum >= right_sum and left_sum >= crossing_sum:
        return left_low, left_high, left_sum
    elif right_sum >= left_sum and right_sum >= crossing_sum:
        return right_low, right_high, right_sum
    else:
        return crossing_low, crossing_high, crossing_sum
    
low, high, max_sum = FIND_MAXIMUM_SUBARRAY(vary, 0, len(vary) - 1)
print(f"Max subarray from index {low} to {high} with sum {max_sum}")

可能递归对于有些看官们来说很抽象，请您不要急，使用黑盒子法，再写递归函数时就假定这个函数已经写好了，于是找到全部在左半边的最大子数组就是

left_low, left_high, left_sum = FIND_MAXIMUM_SUBARRAY(A, low, mid)

好了，以上就是求解最大子数组的全部内容了！

# plot divide and conquer
time_divide_and_conquer = []
for i in range(0, len(vary)):
    start = time.time()
    low, high, max_sum = FIND_MAXIMUM_SUBARRAY(vary, 0, i)
    end = time.time()
    time_divide_and_conquer.append(end - start)

plt.plot(range(1, len(vary) + 1), time_divide_and_conquer, label='Divide and Conquer', color='blue')

# plot force brute
time_force_brute = []
for i in range(0, len(vary)):
    start = time.time()
    low, high, max_sum = force(vary[:i+1])
    end = time.time()
    time_force_brute.append(end - start)
plt.plot(range(1, len(vary) + 1), time_force_brute, label='Force Brute', color='red')
plt.xlabel('Array Size')
plt.ylabel('Time (seconds)')
plt.title('Time Complexity of Max Subarray Algorithms')
plt.legend()
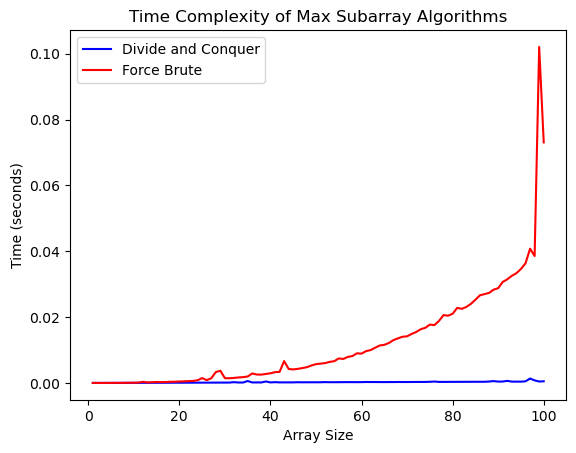
plt.show()

我比较了两种算法的性能差异