蓝桥杯JAVA B组 2016第六题 方格填数

一.题目描述

如下的10个格子

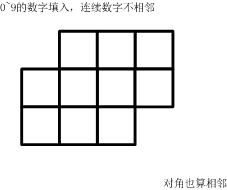
填入0~9的数字。要求：连续的两个数字不能相邻。（左右、上下、对角都算相邻）

 一共有多少种可能的填数方案？

二.思路分析

判断方格加上1会不会等于周围的方格，方格减去一会不会等于周围的方格

以下是对方格作为数组给予相应下标

①  对于这种方格填0~9无重复数字的这一类题目，我们需要有一种全局的思维，因为这样的题目是可以使用全排列来解决的

② 使用全排列来做，首先要生成0~9这四个数字的全排列，每生成一个排列需要进行检查，所以对于这样的题目的套路在于先求解出排列然后对当前排列进行校验，看是否符合题目的要求，假如满足那么我们的计数就加一

而求解全排列又可以使用递归加上回溯的框架来做，即交换当前位置和当前位置后面的位置的元素（包括当前位置）

③ 每生成一个全排列我们使用函数来校验，根据题目中的限定条件来进行一一的判断，对于这道题目来说，判断条件是比较多的，需要细心一点才不会出错

三.代码

public class test1 {
    static int count=0;
    public static void main(String[] args){
        int []arr = {0,1,2,3,4,5,6,7,8,9};
        f(arr,0,arr.length-1);
        System.out.println(count);//答案:1580
    }
    public static void f(int []arr,int start,int end){
        if(start==end){
            //判断条件:方格加上1会不会等于周围的方格，方格减去一会不会等于周围的方格【注意还要判断减一后的情况】
            if(     arr[0]+1!=arr[1]&&arr[0]-1!=arr[1]&&
                    arr[0]+1!=arr[3]&&arr[0]-1!=arr[3]&&
                    arr[0]+1!=arr[4]&&arr[0]-1!=arr[4]&&
                    arr[0]+1!=arr[5]&&arr[0]-1!=arr[5]&&
                    arr[1]+1!=arr[2]&&arr[1]-1!=arr[2]&&
                    arr[1]+1!=arr[4]&&arr[1]-1!=arr[4]&&
                    arr[1]+1!=arr[5]&&arr[1]-1!=arr[5]&&
                    arr[1]+1!=arr[6]&&arr[1]-1!=arr[6]&&
                    arr[2]+1!=arr[5]&&arr[2]-1!=arr[5]&&
                    arr[2]+1!=arr[6]&&arr[2]-1!=arr[6]&&
                    arr[3]+1!=arr[4]&&arr[3]-1!=arr[4]&&
                    arr[3]+1!=arr[7]&&arr[3]-1!=arr[7]&&
                    arr[3]+1!=arr[8]&&arr[3]-1!=arr[8]&&
                    arr[4]+1!=arr[5]&&arr[4]-1!=arr[5]&&
                    arr[4]+1!=arr[7]&&arr[4]-1!=arr[7]&&
                    arr[4]+1!=arr[8]&&arr[4]-1!=arr[8]&&
                    arr[4]+1!=arr[9]&&arr[4]-1!=arr[9]&&
                    arr[5]+1!=arr[6]&&arr[5]-1!=arr[6]&&
                    arr[5]+1!=arr[8]&&arr[5]-1!=arr[8]&&
                    arr[5]+1!=arr[9]&&arr[5]-1!=arr[9]&&
                    arr[6]+1!=arr[9]&&arr[6]-1!=arr[9]&&
                    arr[7]+1!=arr[8]&&arr[7]-1!=arr[8]&&
                    arr[8]+1!=arr[9]&&arr[8]-1!=arr[9]){
                count++;
            }
        }
        //全排列递归回溯
        for(int i=start;i<arr.length;i++){
            int t = arr[i];
            arr[i]=arr[start];
            arr[start]=t;
            f(arr,start+1,arr.length-1);
            t = arr[i];
            arr[i]=arr[start];
            arr[start]=t;
        }
    }
}