回归（二）：缩减系数

回归算法中不管是用线性回归找到最佳拟合直线，还是加权的线性回归算法，我们都是直接用矩阵相乘的方式，直接计算出对应的ω系数，这都是对应训练数据组成的矩阵是可逆的，换句话说X矩阵是满秩的，而对于某些属性个数多余样本个数的样本（样本数据组成矩阵后列数多于行数）组成的矩阵是不满秩，计算(XTX)-1的时候是会出错的。所以为了解决这个问题统计学家们引入了领回归（ridge regression）的概念。

1. 岭回归

岭回归就是在矩阵XTX上加了一个λI，从而使得矩阵非奇异，进而能够对XTX+λI求逆。其中I是一个m×m的单位矩阵，而λ是用户自定义的一个数值。在这种情况下，回归系数的计算公式变成如下公式：

至于为什么叫岭回归，书上是这么说的，供参考：岭回归使用了单位矩阵乘以常量λ，我们观察其中的单位矩阵I，可以看到值1贯穿整个对角线，其余元素全是0。形象地，在0构成的平面上有一条1组成的“岭”，这就是岭回归中的“岭”的由来。

文章前面说了，岭回归的引入是为了解决特征数目多于样本数的情况，但是并不是说特征数目少于样本数就不能用岭回归的方式了，只不过是我们需要从另外一个方面去理解岭回归的概念：

岭回归现在也用于在估计中加入偏差，从而得到更好的估计。这里通过引入λ来限制了所有w的和，通过引入改惩罚项，能够减少不重要的参数，这个基数在统计学中也叫作缩减（这句话是书上的原话，其实我是保持怀疑的，至于为什么，到后面和lasso做下对比就知道了）。

接着引入惩罚项的说：我们先把上面岭回归系数的计算公式还原，从最初的公式看起：

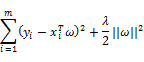
上面公式求导，等0，就可以得到我们前面说的岭回归的回归系数计算公式。但是我们这里只看这个最初的公式，相当于在原有的的平方误差的基础上加入了一项，此项是对ω的约束；正规一点的说法是引入了正则项其中的||ω||2是向量ω的L2范式；ω的L2范式也可以看做是当前模型的复杂度。其实这个引入正则化及其系数，和决策树中引入树的复杂度及其系数的做法是相似的，也是可以防止模型过拟合。

在岭回归中，会有公式： ，即限定了所有回归系数的平方和不能大于λ(λ是一个常数)。在使用普通的最小二乘法回归在当两个或更多的特征相关时，可能会得出一个很大的正系数和一个很大的负系数。正式因为上述限制条件的存在，使岭回归可以避免这个问题。

1. lasso

lasso和岭回归类似，也是对回归系数做了限定，对应的约束条件限制为： ，和岭回归不同的是，这个约束条件用绝对值取代了平方和，专业一点的说法叫L1范式。虽然约束形式只是做了稍作变化，但是结果却大相径庭：在λ足够小的时候，一些系数会因此被迫缩减到0，这个特性可以帮助我们更好的理解数据。但是这个变化却极大的加大了计算的复杂度，因为|ω|是不可导的。

上面我们提到了有些系数会被缩减到0，如果系数是0，那么该项对应的参数值与0相乘也是零，就是对应的特征不起作用，从而可以忽略这个特征，也就是缩减系数；而岭回归中虽然也有可能缩减系数，但是程度远远没有lasso的程度大，所以lasso也可以用来特征选择。

不管是lasso和岭回归，都是对系数做了限制，使其不断缩小。我们知道系数小的模型复杂度就小，因为某一特征值的变化，不会使结果有大的变化，如果系数大的话，某一特征值对结果的影响就比较大了。

其实岭回归和lasso在回归模型中是比较重要的概念，此篇文章的上面只是提到了两者的一些性质以及用法，也并没有十分详细的说。如果想进一步了解，可以网上搜L2和L1正则化，有大神讲的更好，不过我也在另一篇文章《L1和L2正则化》中做了自己简单的总结。

1. 前向逐步回归

前向逐步回归算法可以得到和lasso差不多的效果，但更简单，没有涉及太多的数学理论，也相对容易理解。它是一种贪心算法（所谓的贪心算法，简单说，就是在详细的每一步得到最优的结果），即每一步都尽可能的减少误差，所以一开始所有特征的权重都设为1，然后每一步所做的决策是对某个权重增加或者减少一个很小的值。这里感觉就和梯度下降法有点像了。

首先需要对数据进行标准化，标准化数据的目的是将原来的数据映射到特定的区间。否则的话不同的特征可能有不同的尺度标准，不同权重的下降速度也不一样，并且不同的特征的数值如果数量级相差太大的话，就会在机器学习的结果中占据主要的地位，所以将所有的特征值放到一个区间，增加了可比性，也增加了学习的准确性。

下面写出具体步骤

1. 设定迭代的次数
2. 设定当前的损失值为最大正无穷
3. 循环每个特征值的权重ωi，对其增加或者减少，并计算当前权重下的损失；如果当前权重下的损失小于上一个损失，那么更新当前特征值的权重为ωik，并且更新当前损失值，否则不予更新。
4. 每次迭代都要重新循环计算比较所有的权重值，直到达到相应的循环迭代次数

ωi是第i个特征的权重，ωik是在不断的迭代过程中的权重中间值。我们之间假设过，将所有的权重都设为1，那么ωik在每次循环中就可能是[-1,1]区间中梯度为0.02的一系列值。