矩阵乘法经典应用之置换

学习用矩阵做置换的过程很有趣，我遇到的置换问题最开始的思路就向矩阵发展了，然而很不幸，那题时间卡的紧，用矩阵是超时的做法（反正我没过）。不过我也意外的学习了这样的方法：
经典的置换矩阵：
比如：1 2 3 4 ---> 2 4 1 3

设转换矩阵是A。

给出置换方法：

表示第位置上的字符换到i位置上

所以

通过将置换操作分离出来成快速幂，最后和被操作序列做乘法，缩短时间。估计时间：O(nm) --> O(logn+m)

这是那一道题（注：下面的代码是超时的，我只是想用用矩阵模拟置换而已）

POJ 1026 Cipher

http://poj.org/problem?id=1026

输入：
10
4 5 3 7 2 8 1 6 10 9
1 Hello Bob
1995 CERC

解释：

n

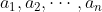
k  string

给出置换方法： .  表示第i位置上的字符换到位置上

所以。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=205;
int n;
char mys[N],cont[N];
struct matrix{
    int m[N][N];
}I;
int add(int a,int b){
    int ans=0;
    while(b){
        if(b&1) ans=ans+a;
        a=a+a;
        b>>=1;
    }
    return ans;
}
matrix operator *(const matrix a,const matrix b){
    matrix ans;
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++){
            ans.m[i][j]=0;
            for(int k=0;k<n;k++){
                ans.m[i][j]+=add(a.m[i][k],b.m[k][j]);  //位置置换不需要模运算。
            }
        }
    }
    return ans;
}
matrix operator ^(const matrix a,const int b){
    matrix ans=I,temp=a;
    int p=b;
    while(p){
        if(p&1) ans=ans*temp;
        temp=temp*temp;
        p>>=1;
    }
    return ans;
}
void show(matrix mp){
    for(int i=0;i<n;i++){
        for(int j=0;j<n;j++)  cout<<mp.m[i][j]<<" ";
        cout<<endl;
    }
}
int main()
{
    //freopen("cin.txt","r",stdin);
    for(int i=0;i<N;i++){
        I.m[i][i]=1;
    }
    while(~scanf("%d",&n)&&n){
        matrix A;   // 默认构造方法，m全是0
        int val;
        for(int i=0;i<n;i++){
            scanf("%d",&val);
            A.m[val-1][i]=1; // 和经典类型相比，列变行 行变列
        }
        int k;
        while(scanf("%d",&k)&&k){
            matrix g=A^k;
            getchar();
            gets(mys);
            int len=strlen(mys);
            while(len<n){
                mys[len++]=' ';
            }
            for(int i=0;i<n;i++){
                cont[i]=0;
                for(int k=0;k<n;k++){
                    cont[i]+=g.m[i][k]*mys[k];
                }
            }
            cont[n]=0;
            printf("%s\n",cont);
        }
    }
    return 0;
}

下面才是正确的解法：
对置换群每个元素寻找循环节。

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=205;
int a[N];
int cir[N];
char str[N];
char ans[N];
bool vis[N];
int main()
{
    //freopen("cin.txt","r",stdin);
    int n;
    while(scanf("%d",&n)&&n){
         for(int i=1;i<=n;i++)
             scanf("%d",&a[i]);

         for(int i=1;i<=n;i++){
             memset(vis,0,sizeof(vis));
             int dex=i;
             int loop=0;
             while(vis[dex]==0){
                 loop++;
                 vis[dex]=1;
                 dex=a[dex];
             }
             cir[i]=loop;
         }

         int k;
         while(scanf("%d",&k)&&k){
            memset(ans,0,sizeof(ans));
            getchar();
            gets(str+1);
            int len=strlen(str+1);
            for(int i=1;i<=n;i++){
                int d=k%cir[i];
                int dex=i;
                for(int j=0;j<d;j++){
                    dex=a[dex];
                }
                if(i>len) ans[dex]=' ';
                else ans[dex]=str[i];
            }
            ans[n+1]=0;
            printf("%s\n",ans+1);
         }
         printf("\n");
    }
    return 0;
}

来一个可以用矩阵置换的：

 

  
P1049送给圣诞夜的礼品
  

 
 

  

   

    https://vijos.org/p/1049
   
   

    
输入：
    
7 5 8
6 1 3 7 5 2 4
3 2 4 5 6 7 1
7 1 3 4 5 2 6
5 6 7 3 1 2 4
2 7 3 4 6 1 5
解释：
   
   

    n,m,k
   
   

    m行n列的置换矩阵
    

   
   

    求解原序列为1,2,3,……,n的序列经过置换矩阵操作后的新序列。注意：每一行就是一次置换操作。
    
6 1 3 7 5 2 4 就是把6位置上的元素换到1位置上，1位置上的元素换到2位置上…… 经典的置换操作, .
粗略的讲就是 B=(1,2,3……n)'


   
  
 

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int N=105;
struct matrix{
    int m[N][N];
    int nn,mm;
    matrix operator =(const matrix a){
         nn=a.nn;
         mm=a.mm;
         for(int i=0;i<a.nn;i++){
             for(int j=0;j<a.mm;j++){
                m[i][j]=a.m[i][j];
             }
        }
        return *this;
    }
}mp[15],I,old;
matrix multi(matrix a,matrix b){
    matrix ans;
    ans.nn=a.nn;
    ans.mm=b.mm;
    for(int i=0;i<a.nn;i++){
        for(int j=0;j<b.mm;j++){
            ans.m[i][j]=0;
            for(int k=0;k<a.mm;k++){
                ans.m[i][j]+=a.m[i][k]*b.m[k][j];
            }
        }
    }
    return ans;
}
matrix power(matrix a,int b){
    matrix ans=I,temp=a;
    int p=b;
    while(p){
        if(p&1) ans=multi(ans,temp);
        temp=multi(temp,temp);
        p>>=1;
    }
    return ans;
}
void show(matrix v){
    cout<<"show: "<<endl;
    for(int i=0;i<v.nn;i++){
        for(int j=0;j<v.mm;j++) cout<<v.m[i][j]<<" ";
        cout<<endl;
    }
}
int main()
{
    //freopen("cin.txt","r",stdin);
    for(int i=0;i<N;i++){
        I.m[i][i]=1;
        old.m[i][0]=i+1;
    }

    int n,m,k;
    while(~scanf("%d%d%d",&n,&m,&k)){
        old.nn=n;
        old.mm=1;
        I.nn=n;
        I.mm=n;
        memset(mp,0,sizeof(mp));
        matrix A=I;
        int dex=0;
        for(int i=0;i<m;i++){
            mp[i].nn=mp[i].mm=n;
            for(int j=0;j<n;j++){
                scanf("%d",&dex);
                mp[i].m[j][dex-1]=1;
            }
            A=multi(mp[i],A);
        }
        A=power(A,k/m);
        k=k%m;
        matrix ans=multi(A,old);
        //show(ans);
        for(int i=0;i<k;i++) ans=multi(mp[i],ans);
        //show(ans);
        for(int i=0;i<n-1;i++){
            printf("%d ",ans.m[i][0]);
        }
        printf("%d\n",ans.m[n-1][0]);
    }
    return 0;
}