卷积神经网络--AlexNet

AlexNet

AlexNet发展史

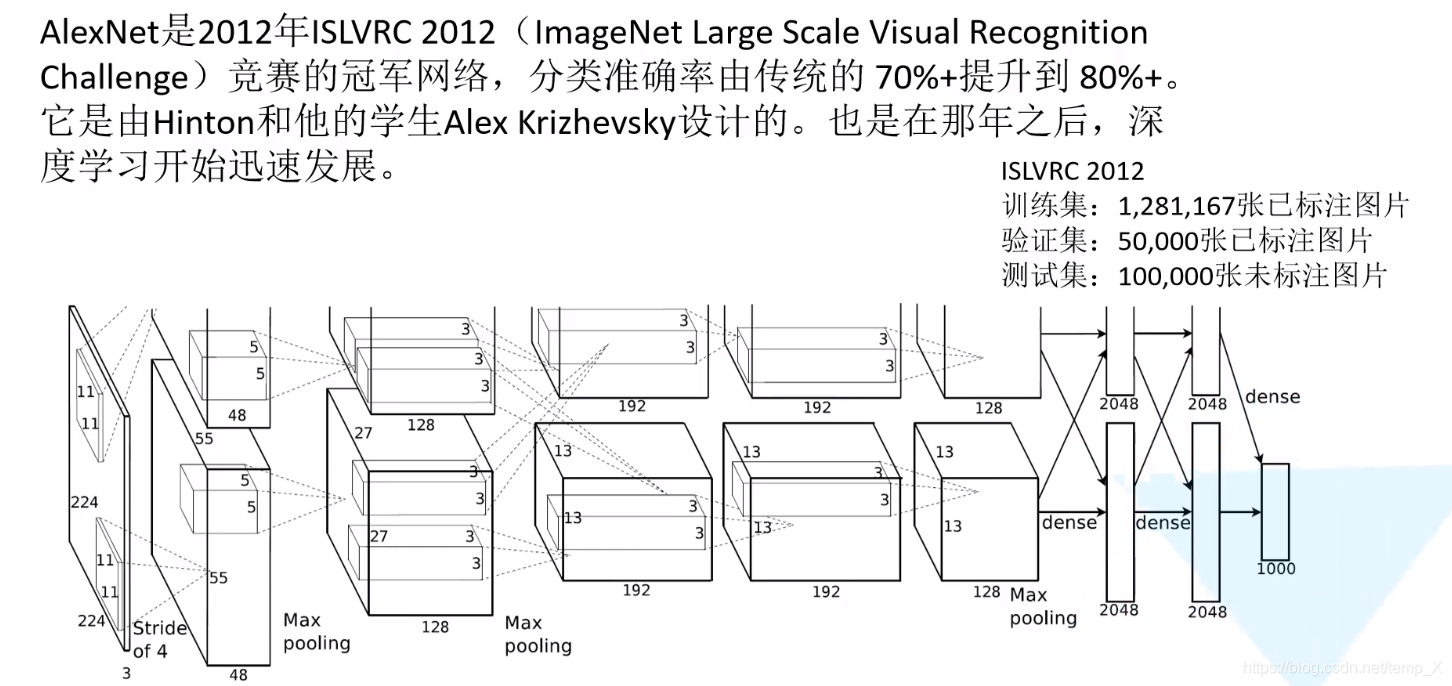
AlexNet网络亮点：

1.首次利用GPU加速训练；
2.使用了ReLU激活函数，而不是传统的sigmod和Tanh激活函数；
3. 使用了LRN局部相应归一化；
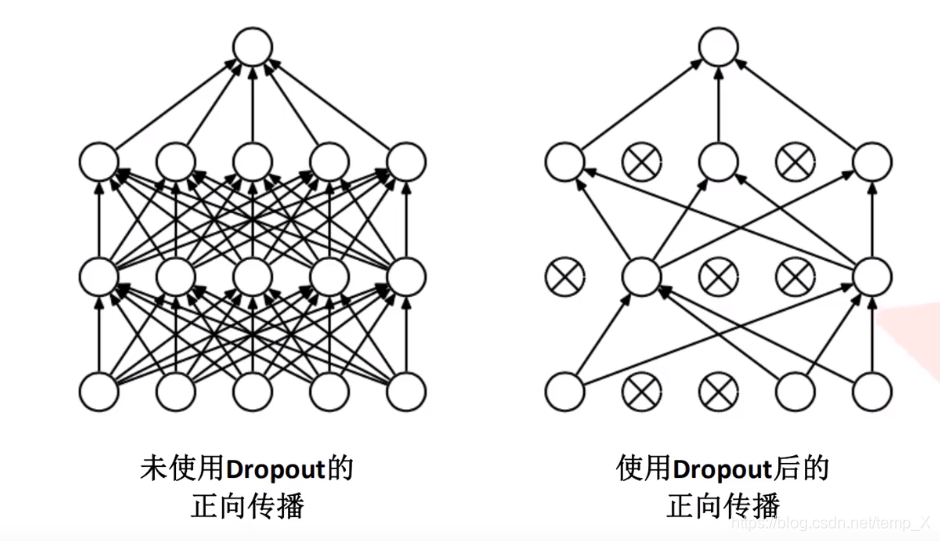
4.在全连接层中使用了Dropout随机失活神经元操作，减少过拟合。

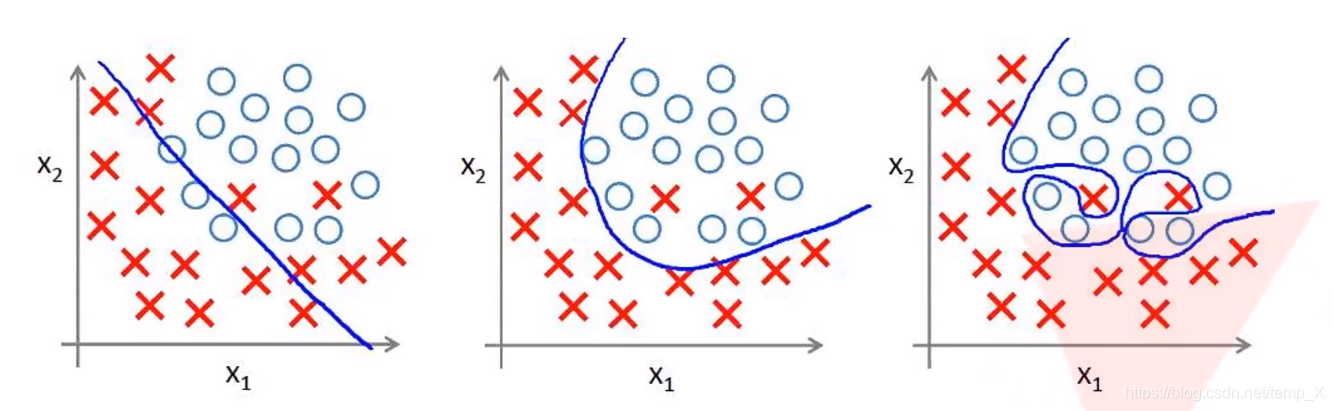
过拟合:

       根本原因是特征维度过多，模型假设过于复杂，参数过多，训练数据过少，噪声过多，导致拟合的函数完美的预测训练集，但对新数据的测试集预测结果差。过度的拟合了训练数据，而没有考虑到泛化能力。

使用Dropout作用

使得网络在正向传播过程中随机失活一部分神经元
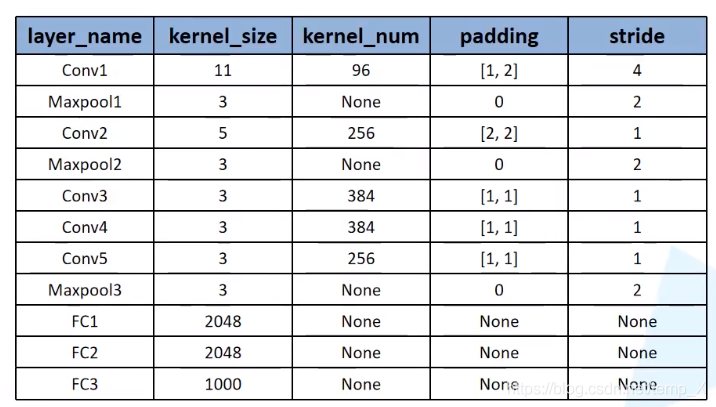
卷积后的矩阵大小计算公式

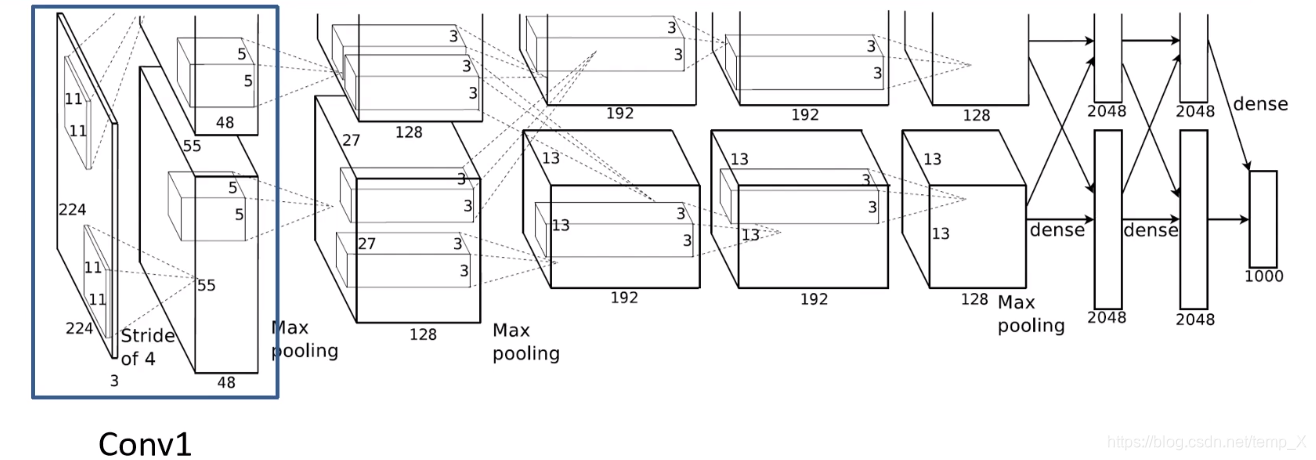
conv1:

kernels:48*2=96；kernel_size:11；padding:[1, 2]；stride:4
input_size: [224, 224, 3]
N = (W − F + 2P ) / S + 1=[224-11+(1+2)]/4+1=55
output_size: [55, 55, 96]

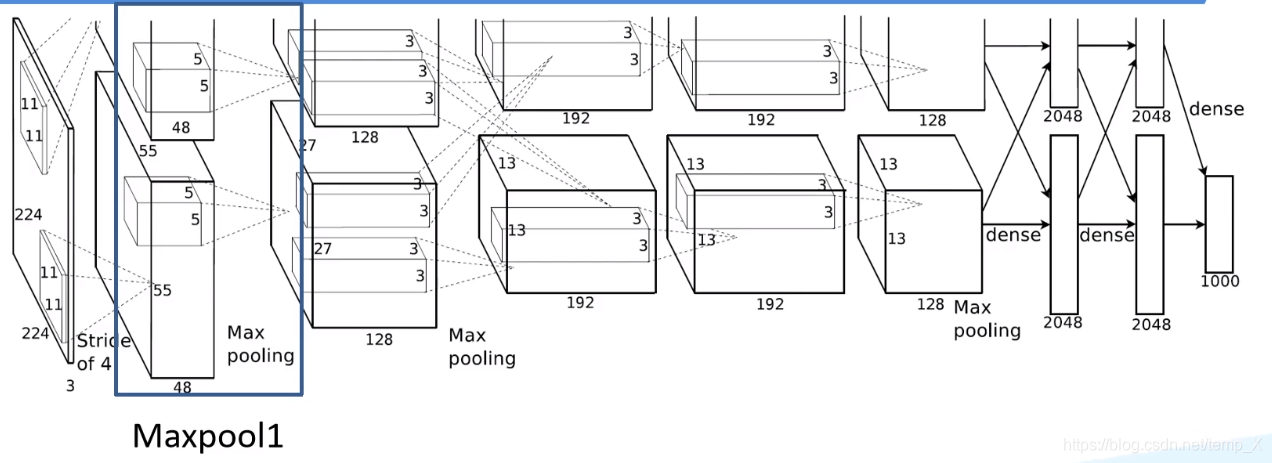
Maxpool1:

kernel_size:3；pading: 0；stride:2;
input_size: [55, 55, 96]
N = (W − F + 2P ) / S + 1=(55-3)/2+1=27
output_size: [27, 27, 96]

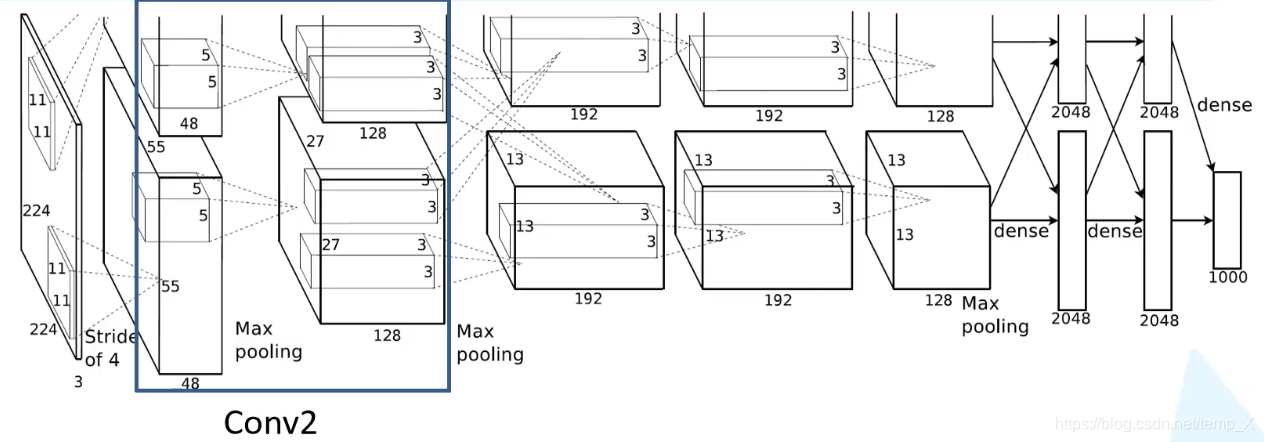
Conv2:

kernels:128*2=256；；kernel_size:5；padding: [2, 2]；stride:1
input_size: [27, 27, 96]
N = (W − F + 2P ) / S + 1=(27-5+4)/1+1
output_size: [27, 27, 256]

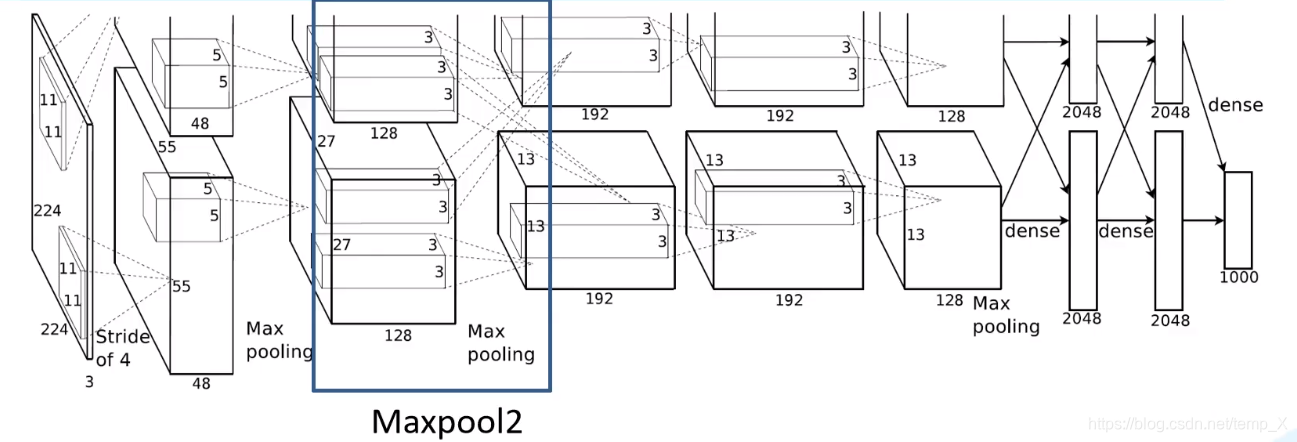
Maxpool2:

kernel_size:3；pading: 0；stride:2;
input_size: [27,27, 256]
N = (W − F + 2P ) / S + 1=(27-3)/2+1=13
output_size: [13, 13, 256]

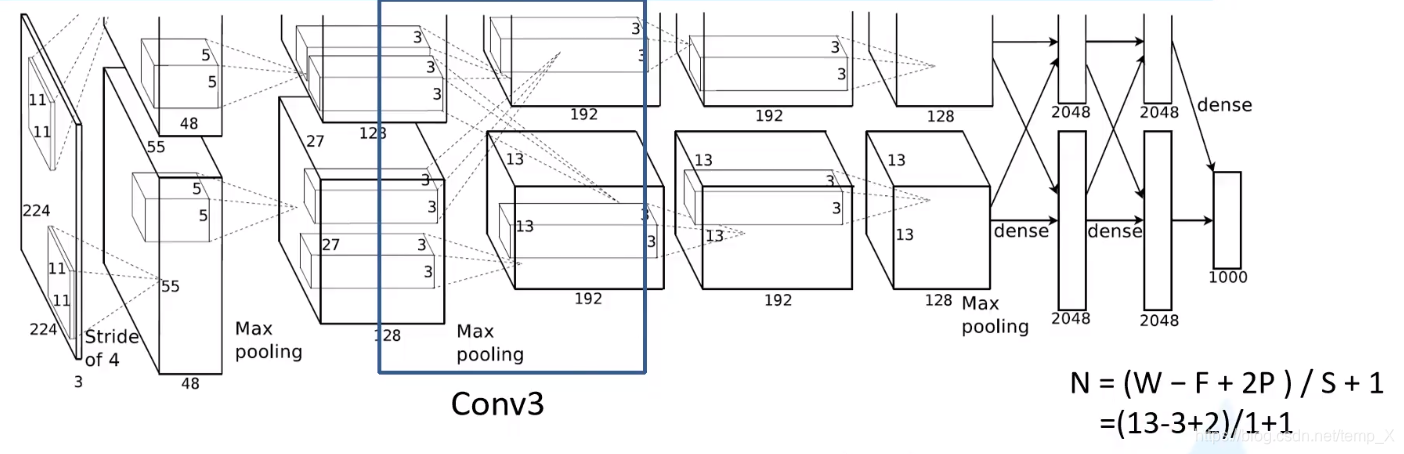
Conv3:

kernels:192*2=384；；kernel_size:3；padding: [1, 1]；stride:1
input_size: [13, 13, 256]
N = (W − F + 2P ) / S + 1=(13-3+2)/1+1
output_size: [13, 13, 384]

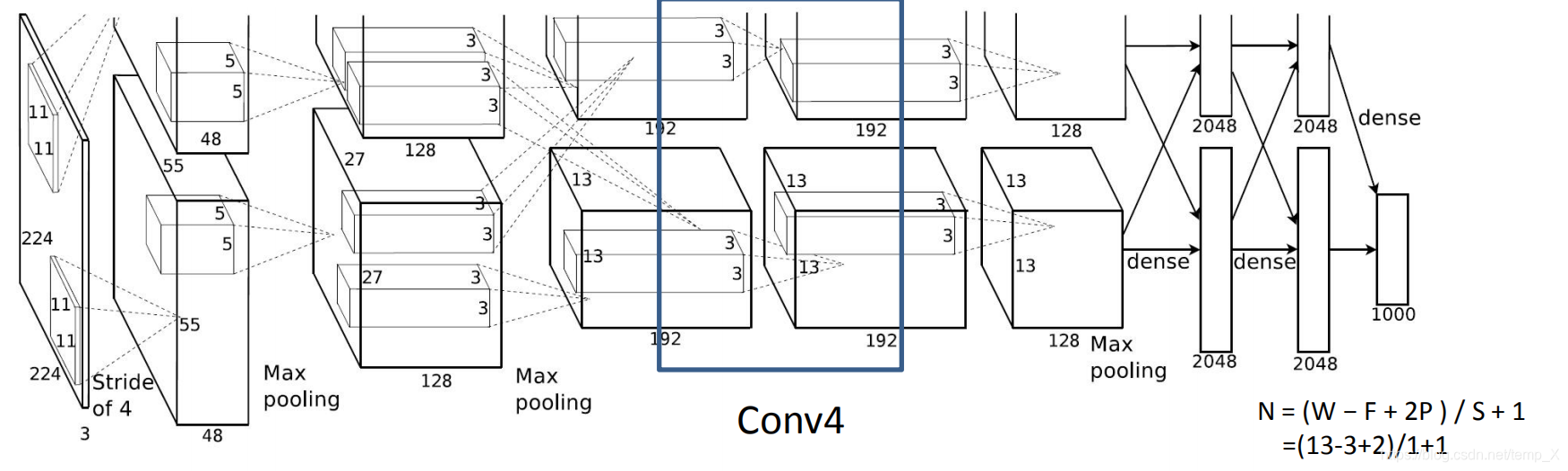
Conv4:

kernels:192*2=384；；kernel_size:3；padding: [1, 1]；stride:1
input_size: [13, 13, 384]
N = (W − F + 2P ) / S + 1=(13-3+2)/1+1=13
output_size: [13, 13, 384]

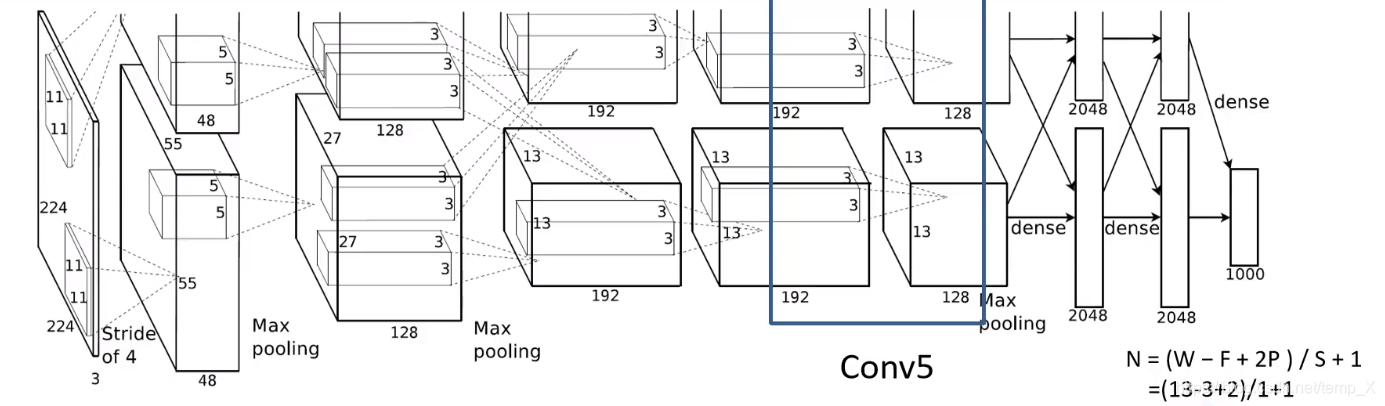
Conv5:    

kernels:128*2=256；；kernel_size:3；padding: [1, 1]；stride:1
input_size: [13, 13, 384]
N = (W − F + 2P ) / S + 1=(13-3+2)/1+1=13
output_size: [13, 13, 256]

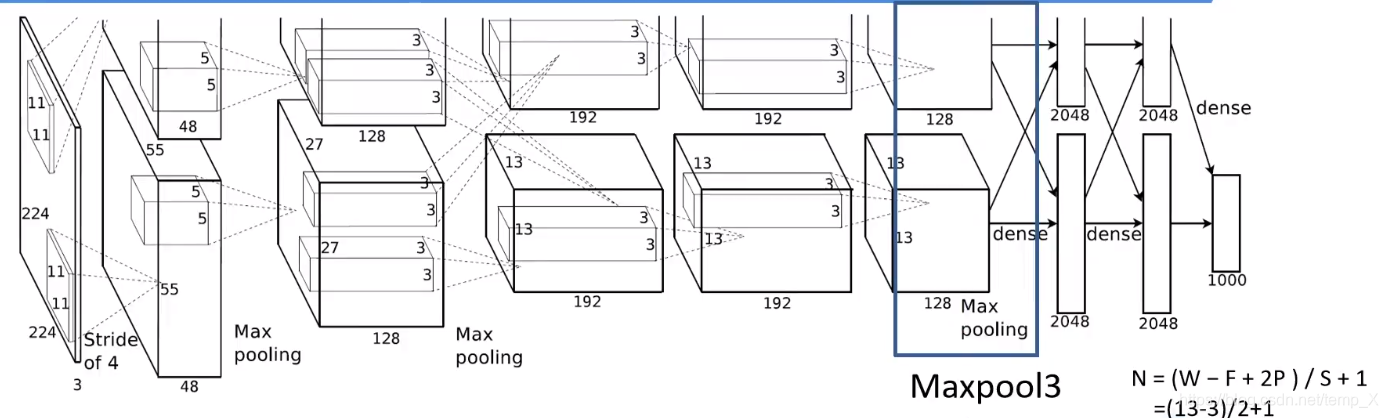
Maxpool3:    

kernel_size:3；pading: 0；stride:2;
input_size: [13,13, 256]
N = (W − F + 2P ) / S + 1=(13-3)/2+1=6
output_size: [6, 6, 256]

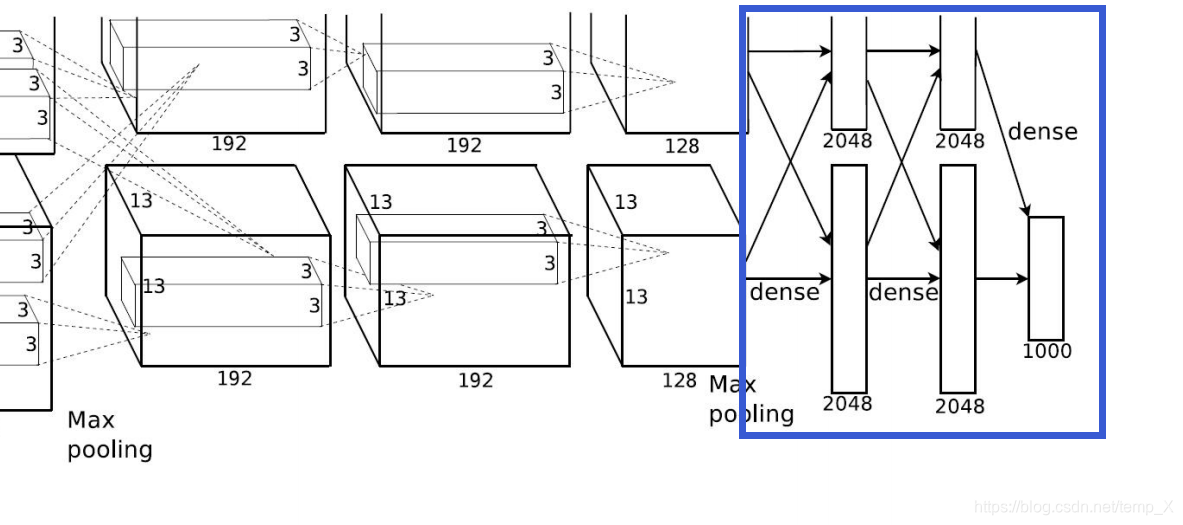
三个全连接层：    

Full Connection1：

nodes=2048
input_size=[6 * 6 * 256]   output=[2048]

Full Connection2：    

nodes=2048
input_size=[2048]   output=[2048]

Full Connection3：    

nodes=1000
input_size=[2048]   output=[1000]

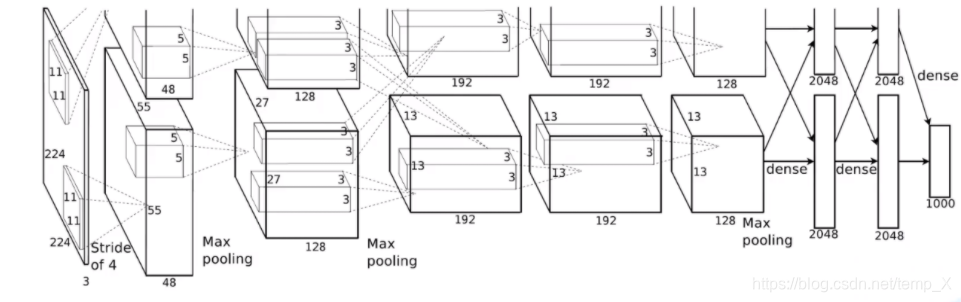
完整网络结构

使用的花分类数据集