NOI2019模拟赛 T1牛油果

最新推荐文章于 2025-12-15 09:15:21 发布

原创最新推荐文章于 2025-12-15 09:15:21 发布 · 1.3k 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #题解

题解专栏收录该内容

348 篇文章

订阅专栏

文章描述了一个关于牛油果坚固程度测试的数学问题，通过动态规划的方法解决。原始算法的时间复杂度为O(n^3)，经过优化后降低到O(n^2)甚至更优。问题的关键在于找到最小实验次数来确定所有牛油果的坚固程度上限。

题目描述

牛油果是一种神秘的水果，其具有一个坚固程度 $x≥0x\geq 0$ ：即从高度不超过 $x$ 米的地方掉下来都不会受损，否则就会破碎。

现在有 $n$ 个牛油果可以用来做实验，如果某个牛油果在一次实验中破碎了就不能继续做实验，否则就可以继续拿来做实验。

假设给出的牛油果坚固程度相同，且已知它们的坚固程度不超过 $m$ ，现在要求最坏情况下至少做多少次实验可以得知它们的坚固程度。

输入格式

一行一个 $t$ ，表示数据组数。

一行两个正整数 $n, m$ 。

输出格式

输出 $t$ 行，第 $i$ 行一个正整数表示第 $i$ 组数据的答案。

样例输入

2
1 2
2 10

样例输出

2
4

数据规模

对于 $10%10\%$ 的数据， $n,m,t≤10n,m,t\leq 10$
对于 $30%30\%$ 的数据， $n,m,t≤50n,m,t\leq 50$
对于 $60%60\%$ 的数据， $n,m,t≤500n,m,t\leq 500$
对于 $100%100\%$ 的数据， $n,m,t≤5000n,m,t\leq 5000$

题解

设 $f_{i,j}$ 表示有 $i$ 个牛油果，坚固程度不超过 $j$ 的最少的实验次数， $f$ 的初值为 $f_{i,0}=0$ ， $f0,i=+∞f_{0,i}=+\infty$ 。

考虑转移，假设此时将一个牛油果从 $k$ 米高的地方扔下来，则

如果碎了，那么牛油果的坚固程度不超过 $k - 1$ ，还剩 $i - 1$ 个牛油果，则需要的次数为 $f_{i-1,k-1}+1$
如果没碎，那么牛油果的坚固程度在 $k$ 到 $j$ 之间，还剩 $i$ 个牛油果，在 $k$ 到 $j$ 之间测试坚固程度等价于在 $0$ 到 $j - k$ 之间测试坚固程度，所以需要的次数为 $f_{i,j-k}+1$

所以转移式为

$fi,j=min⁡k=1j{max⁡(fi−1,k−1,fi,j−k)+1}f_{i,j}=\min\limits_{k=1}^j\{\max(f_{i-1,k-1},f_{i,j-k})+1\}$

得到所有的 $f$ 值，即可 $O (1)$ 输出答案。

这样做的时间复杂度为 $O(n^3)$ ，会TLE。

code

#include<bits/stdc++.h>
using namespace std;
const int N=5000;
int t,n,m,now;
long long f[5005][5005]; 
int main()
{
	f[0][0]=0;
	for(int i=1;i<=N;i++) f[0][i]=1e18;
	for(int i=1;i<=N;i++){
		f[i][0]=0;
		for(int j=1;j<=N;j++){
			f[i][j]=1e18;
			for(int k=1;k<=j;k++){
				f[i][j]=min(f[i][j],max(f[i][j-k],f[i-1][k-1])+1);
			}
		}
	}
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		printf("%lld\n",f[n][m]);
	}
	return 0;
}

我们考虑优化。

对于求 $f_{i,j}$ ，需要用到的数为 $f_{i-1,k-1}$ 和 $f_{i,j-k}$ ，其中 $1≤k≤j1\leq k\leq j$ 。我们发现随着 $k$ 的增大， $f_{i-1,k-1}$ 单调递增（不严格）， $f_{i,j-k}$ 单调递减（不严格）。那么它们的图象大致如下

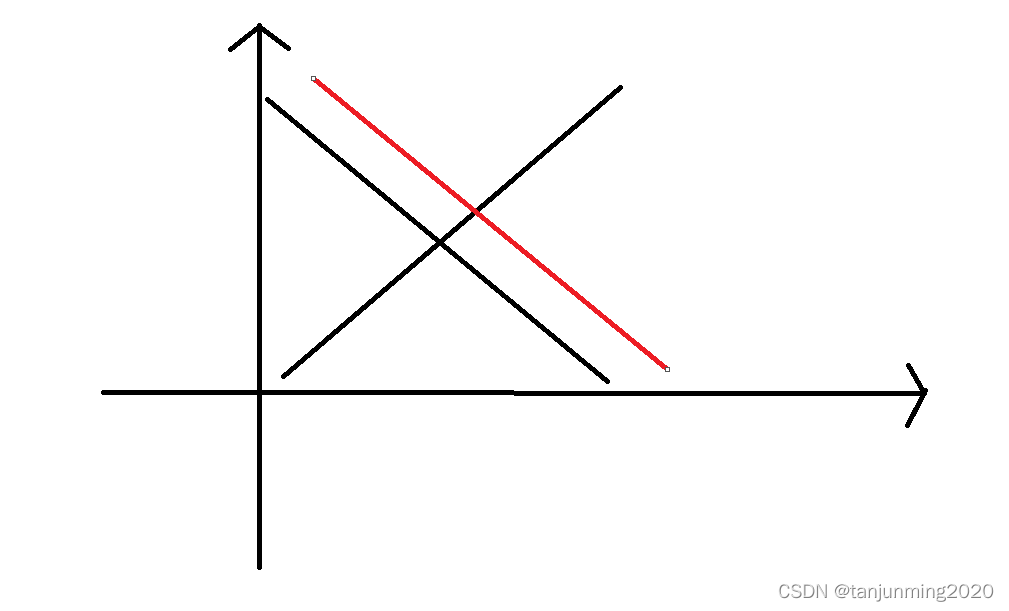
在这里插入图片描述
$j$ 增加了 $1$ 之后， $f_{i-1,k-1}$ 部分不变， $f_{i,j-k}$ 向右平移一位。我们可以发现， $f_{i,j+1}$ 选择的 $k$ 一定在 $f_{i,j}$ 选择的 $k$ 的右边（不严格），所以 $k$ 的枚举可以省去。

在这里插入图片描述

时间复杂度为 $O(n^2)$ 。

code

#include<bits/stdc++.h>
using namespace std;
const int N=5000;
int t,n,m,now;
long long f[5005][5005]; 
int main()
{
//	f[0][0]=0;
//	for(int i=1;i<=N;i++) f[0][i]=1e18;
//	for(int i=1;i<=N;i++){
//		f[i][0]=0;
//		for(int j=1;j<=N;j++){
//			f[i][j]=1e18;
//			for(int k=1;k<=j;k++){
//				f[i][j]=min(f[i][j],max(f[i][j-k],f[i-1][k-1])+1);
//			}
//		}
//	}
	f[0][0]=0;
	for(int i=1;i<=N;i++) f[0][i]=1e18;
	for(int i=1;i<=N;i++){
		f[i][0]=0;
		now=0;
		for(int j=1;j<=N;j++){
			while(now+1<=j-1&&max(f[i][now+1],f[i-1][j-1-now-1])<=max(f[i][now],f[i-1][j-1-now])) ++now;
			f[i][j]=max(f[i][now],f[i-1][j-1-now])+1;
		}
	}
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		printf("%lld\n",f[n][m]);
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}

其实还有一个小优化，因为我们可以二分查找坚固程度，所以最多只需要 $log⁡m\log m$ 次即可得出牛油果的坚固程度， $log⁡m≤13\log m\leq 13$ 。也就是说，我们的 $i$ 只需从 $1$ 枚举到 $13$ 即可，不需要上述的优化。

时间复杂度为 $O(13n^2)$ ，勉强能过。

code

#include<bits/stdc++.h>
using namespace std;
const int N=5000;
int t,n,m,now;
long long f[15][5005]; 
int main()
{
	f[0][0]=0;
	for(int i=1;i<=N;i++) f[0][i]=1e18;
	for(int i=1;i<=13;i++){
		f[i][0]=0;
		for(int j=1;j<=N;j++){
			f[i][j]=1e18;
			for(int k=1;k<=j;k++){
				f[i][j]=min(f[i][j],max(f[i][j-k],f[i-1][k-1])+1);
			}
		}
	}
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		if(n>13) n=13;
		printf("%lld\n",f[n][m]);
	}
	return 0;
}

如果你将两种优化方法结合，那么你的代码会跑得飞快。

时间复杂度为 $O (13 n)$ 。

#include<bits/stdc++.h>
using namespace std;
const int N=5000;
int t,n,m,now;
long long f[15][5005]; 
int main()
{
	f[0][0]=0;
	for(int i=1;i<=13;i++) f[0][i]=1e18;
	for(int i=1;i<=13;i++){
		f[i][0]=0;
		now=0;
		for(int j=1;j<=N;j++){
			while(now+1<=j-1&&max(f[i][now+1],f[i-1][j-1-now-1])<=max(f[i][now],f[i-1][j-1-now])) ++now;
			f[i][j]=max(f[i][now],f[i-1][j-1-now])+1;
		}
	}
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);
		if(n>13) n=13;
		printf("%lld\n",f[n][m]);
	}
	fclose(stdin);
	fclose(stdout);
	return 0;
}