青蛙跳台阶问题

青蛙跳台阶：

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

青蛙一次可以跳一阶，也可以跳两阶，所以：

当台阶数为1时，有一种跳法，即f(1) = 1;；

当台阶数为2时，有两种跳法,即f(2) = 2；

当台阶数为3时，有三种跳法，即f(3) = 3 = f(1) + f(2);

...

当台阶数为n时f(n) = f(n-1) +f(n-2)

即可以看出规律

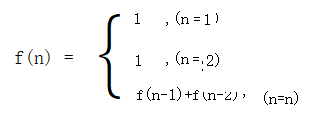
class Solution {
public:
    int jumpFloor(int number) {
        if(number == 1)
            return 1;
        if(number == 2)
            return 2;
        int res = 0;
        int a = 1;
        int b = 2;
        for(int i = 3;i <= number; ++i)
        {
           res = a + b;
            a = b;
            b = res;
        }
        return res;
    }
};

青蛙变态跳台阶：

一只青蛙一次可以跳上1级台阶，也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

分析：

f(0) = 1;

f(1) = 1;

f(2) = f(2-1)+f(2-2),其中f(2-2)表示一次跳两阶的跳法,f(2-1)表示一次跳一阶的跳法

f(3) = f(3-1)+f(3-2)+f(3-3)

...

f(n) = f(n-1)+f(n-2)+f(n-3)+...+f(2)+f(1)+f(0)

说明：

1. f(n)表示n个台阶有一次跳1，2，3...n阶的跳法数
2. n=1时，只有一种跳法，f(1)=1
3. n=2时，有两种跳法，一次一阶或者一次两阶，即f(2)=f(2-1)+f(2-2)
4. 同理n=3,f(3) = f(3-1)+f(3-2)+f(3-3)
5. 当n=n-1时f(n-1)=f(n-2)+f(n-3)+...+f(2)+f(1)+f(0)
6. 当n=n时f(n) = f(n-1)+f(n-2)+f(n-3)+...+f(2)+f(1)+f(0)

用f(n）- f(n-1)= f(n-1)

即f(n) = 2*f(n-1)

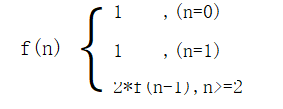
相关代码：

class Solution {
public:
    int jumpFloorII(int number) {
        if(number == 0 || number == 1)
            return 1;
        else
        {
            return 2*jumpFloorII(number - 1);
        }
    }
};