浮点的表示方法与存储

目录

1.1：表示方法；
1.2：计算机中的存储方式；
1.3：浮点数产生精度误差原因；
1.4：float(单精度)、double、long double如何选择

1.1表示方法

代码中，可以用多种形式书写浮点常量。基本形式为：有符号的数字(包括小数点)，后面紧跟e或E，最后是一个有符号数表示10的指数。例：
-1.56E+12;
2.84e-3;
实际书写，部分内容可以省略，但为方便阅读，不建议省略；
省略详情可参考《C Primer Plus》中“float 、double和long double”章节；

1.2 存储方式

浮点数存储（IEEE 754 标准）以 单精度浮点数（32 位） 为例，存储步骤如下：
(1) 转换为二进制
整数部分：7 的二进制为 111。
小数部分：0.12 的二进制转换：
0.12 × 2 = 0.24 → 0
0.24 × 2 = 0.48 → 0
0.48 × 2 = 0.96 → 0
0.96 × 2 = 1.92 → 1
0.92 × 2 = 1.84 → 1
0.84 × 2 = 1.68 → 1
0.68 × 2 = 1.36 → 1
…（无限循环，无法精确表示）
因此，0.12 ≈ 0.00011110101110000101…（二进制）。
合并整数和小数部分：
7.12 ≈ 111.00011110101110000101…（二进制）。
(2) 规范化二进制数
将二进制数转换为科学计数法形式 1.xxxx × 2^e：
111.00011110… → 1.1100011110… × 2^2
（左移两位，指数 e = 2）。
(3) IEEE 754 单精度存储格式
单精度浮点数（32 位）分为三部分：
符号位（1 位）：正数为 0，负数为 1。此处为 0。
指数（8 位）：实际指数 e = 2，需加上 偏移量 127(此为IEEE754标准内容，大致是为了方便负指数的存储) → 2 + 127 = 129 → 二进制 10000001。
尾数（23 位）：取科学计数法中的小数部分 1100011110…( IEEE 754规定浮点数必须表示为 规范化形式,，整数 部分固定为1，因此无需显式存储)，截断或舍入至 23 位。
(4) 最终二进制表示
符号位 | 指数部分 | 尾数部分
0 | 10000001 | 11000111101011100001010
(5) 十六进制表示
将二进制转换为十六进制：
0x40E3D70A（实际值约为 7.1199998856，存在精度误差）。

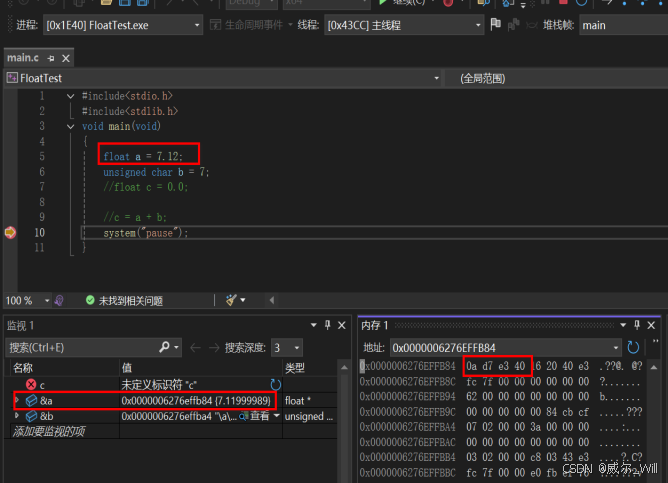
1.3 浮点数产生精度误差原因

二进制小数对应的十进制值；
在二进制中，小数点后的每一位代表的是 2 的负幂次方：
第一位（小数点后第一位）表示 2−1（即 1/2）。
第二位表示 2−2（即 1/4）。
第三位表示 2−3（即 1/8），以此类推。
因此：
二进制的小数仅能表示1/2,1/4,1/8等；其他的小数则为二进制的无限循环，故会产生误差；

1.4 float(单精度)、double、long double如何选择

(1) float：
通常系统为32个bit， 1个bit表示符号，8个bit表示指数，23个bit表示有效数字；
2的23 次方 为 8,388,608，若软件中浮点数的整数值接近800万时，23个bit全被用作存储整数，无剩余bit来存储小数，则小数部分被舍弃了，会造成精度误差；

(2) double：
通常系统为64个bit，1个bit表示符号，16个bit表示指数(有的系统仍为8个bit)，47个bit表示有效数字；
2 的 47 次方 为 140,737,488,355,328，即：140万亿，常规系统不会有这么大的数据，故double的精度足矣；