一、二叉树
每个节点最多只有两个分支。
冒泡、选择、快速、插入等排序算法基于数组的,查找方便,插入删除麻烦。用链表的话,插入删除方便、但是查找麻烦了,每次都需要从头向尾查找。
中和数组和链表那就是平衡二叉树。
平衡二叉树由于每次的插入删除都会导致过多的旋转损失性能,所以引入红黑树。
红黑树不需要保持完全平衡,而是通过红黑平衡来保证最长路径和最短路径保持在2倍高度范围内。
一个节点存储一个数据使得存储效率不高,从而引入B树,2-3树,2-3-4树,使一个节点能存储多个数值。
普通二叉树
不一定是有序的
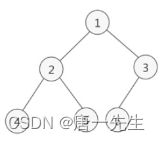
二叉查找树
有序二叉树(二叉搜索树),不一定平衡,查找效率退会为o(n)
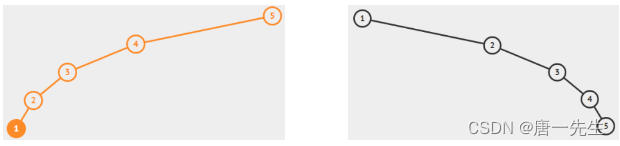
平衡二叉树
平衡,查找效率高(logN)。任意节点的两个子树的高度差不超过1
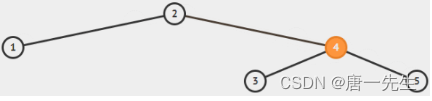
不平衡时需要旋转,旋转规则(定义P或PA为父节点,PP为祖父节点,PPP为祖父的父节点,PC为子节点,PL为左孩子,PR为右孩子):
- 先判断是哪一棵子树不平衡
每次插入新节点,需要判断插入后其祖父节点的左右支树高度差是否大于1,大于1则需要旋转祖父节点的这棵子树。 - 判断这个子树是否是有序的3点1线,不是的话先自旋变成有序的三点一线。
- 判断旋转子树的PP节点有几个孩子
a. 只有一个孩子,只在本子树中自旋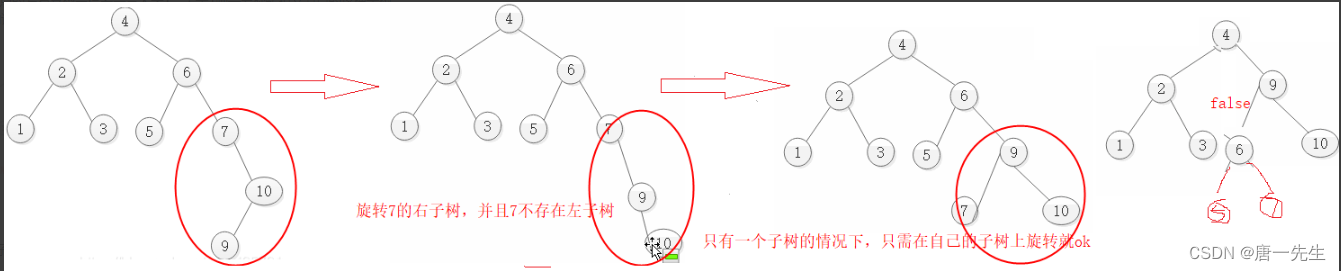
b. 有2个孩子时,保证另一子树不动,旋转子树的P节点往PPP位置提。PPP变成P的左孩子,PC变成P的左孩子的右孩子。
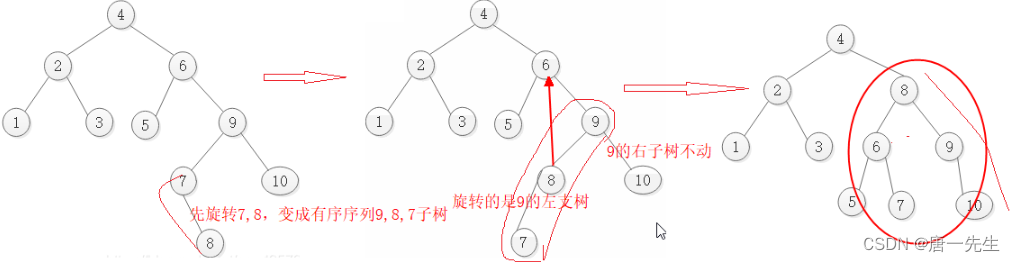
断开8,9:修改9的PL指针为NULL, 8的P为NULL,
7,8自旋:8的PL为7, 7的P为8,7的PL为空;
往上提8:8的P指针=9的PP(为NULL的话就是根节点);
变更8,9的关系:8的PR为9, 9的P为8;
变更8的左孩子:临时保持7,8的PL改为6(PPP),6的P为8;
变更6(PPP)的右孩子:6的PR为7,7的P为6,;
总共改动的节点:4,6,7,8,9
红黑树
Red-Black Tree,一种特殊的二叉查找树。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。
通过任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡
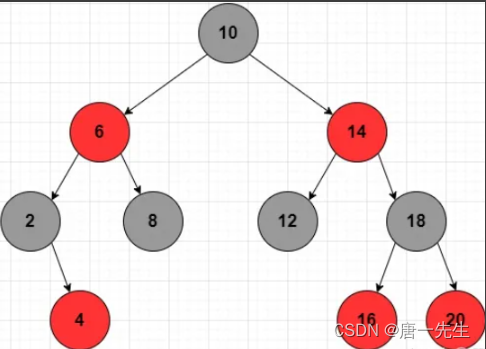
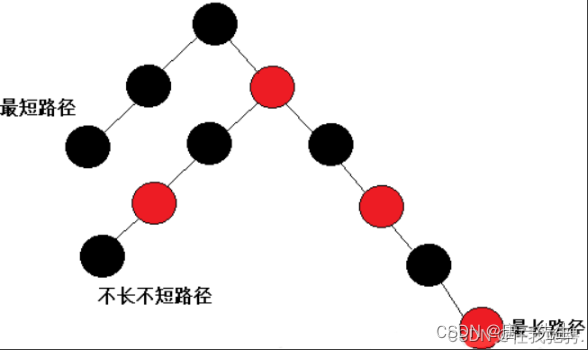
插入同平衡二叉树差不多,唯一不同的就是着色是红黑平衡。
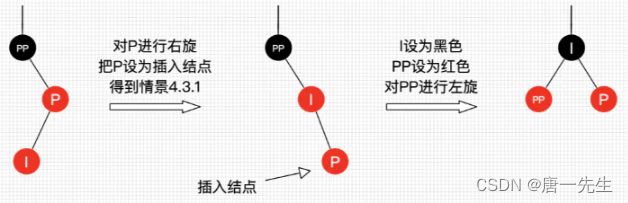
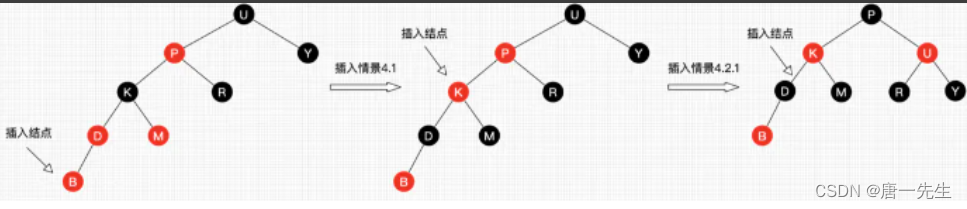
删除比插入复杂很多,但原理都是保证二叉树平衡的同时保证红黑平衡。

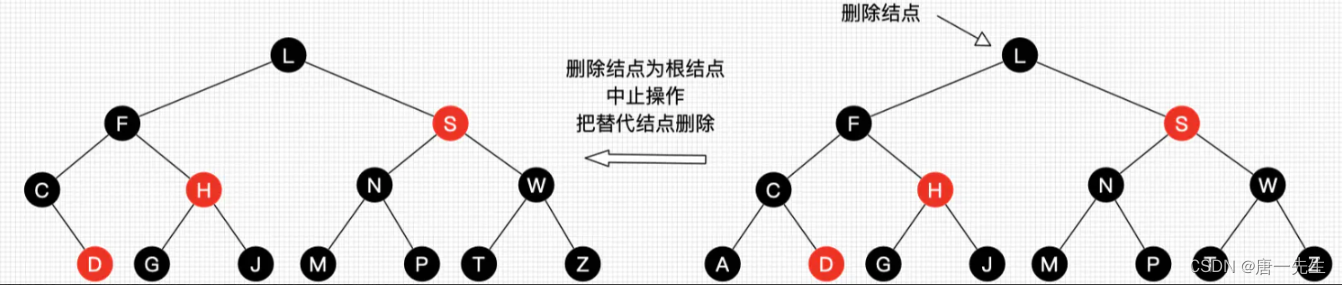
上图,要删除A节点,首先是C树会黑少导致不平衡,要是C树平衡,那就只能D变红。
对C的兄弟H,H认为C少了一个黑,为了保持平衡,H树也需要减少一个黑,那就只能H变红才能保持H树的平衡。
同理对于F的兄弟S为了保持平衡也要减少一个黑,那就是统一在S上减,把S变成红,这样整棵树L才能在删除A之后保持平衡。
二、B树
允许一个节点可以有多于两个子节点,同时,也是自平衡的,叶子节点的高度都是相同。
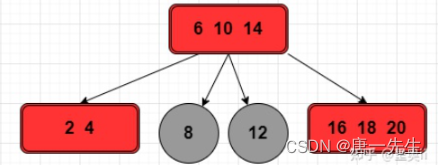




 文章介绍了二叉树的不同类型,包括普通二叉树、二叉查找树、平衡二叉树以及红黑树。平衡二叉树和红黑树为了解决查找效率和插入删除的平衡问题而设计,其中红黑树通过颜色平衡策略保持接近平衡。B树作为一种多路自平衡查找树,允许节点有多个子节点,所有叶子节点高度相同,也保持了查找效率。文章还探讨了插入和删除操作对树平衡的影响。
文章介绍了二叉树的不同类型,包括普通二叉树、二叉查找树、平衡二叉树以及红黑树。平衡二叉树和红黑树为了解决查找效率和插入删除的平衡问题而设计,其中红黑树通过颜色平衡策略保持接近平衡。B树作为一种多路自平衡查找树,允许节点有多个子节点,所有叶子节点高度相同,也保持了查找效率。文章还探讨了插入和删除操作对树平衡的影响。

















 2077
2077

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










