力扣105\106 从前序与中序遍历序列构造二叉树、从中序与后序遍历序列构造二叉树

构造二叉树的一个关键点在于，先创建根节点，然后循环创建左子树和右子树！

# 法一：
# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:

        if preorder is None:
            return None
        index = {}  # 记录位置
        n = len(preorder)
        for i, v in enumerate(inorder):
            index[v] = i
        def tree(p_left, p_right, i_left, i_right):
            if p_left > p_right or i_left > i_right:
                return None
            # 构建新节点
            root = TreeNode(preorder[p_left])
            # 左子树的长度
            i_root = index[preorder[p_left]]
            left_tree_len = i_root - i_left
            # 递归创建左子树
            root.left = tree(p_left+1, p_left+left_tree_len, i_left, i_root-1)

            # 递归创建右子树
            root.right = tree(p_left+left_tree_len+1, p_right, i_root+1, i_right)
            return root

        return tree(0,n-1,0,n-1)
# 法二
class Solution:
    def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
        if preorder is None:
            return None

        def create_root(preorder, inorder):
            if len(inorder) == 0 or len(preorder)==0:
                return None
            cur_root = preorder[0]
            m = inorder.index(cur_root)
            root = TreeNode(cur_root)
            root.left = create_root(preorder[1:1+len(inorder[:m])], inorder[:m])
            root.right = create_root(preorder[1+len(inorder[:m]):], inorder[m+1:])
            return root

        return create_root(preorder, inorder)
        

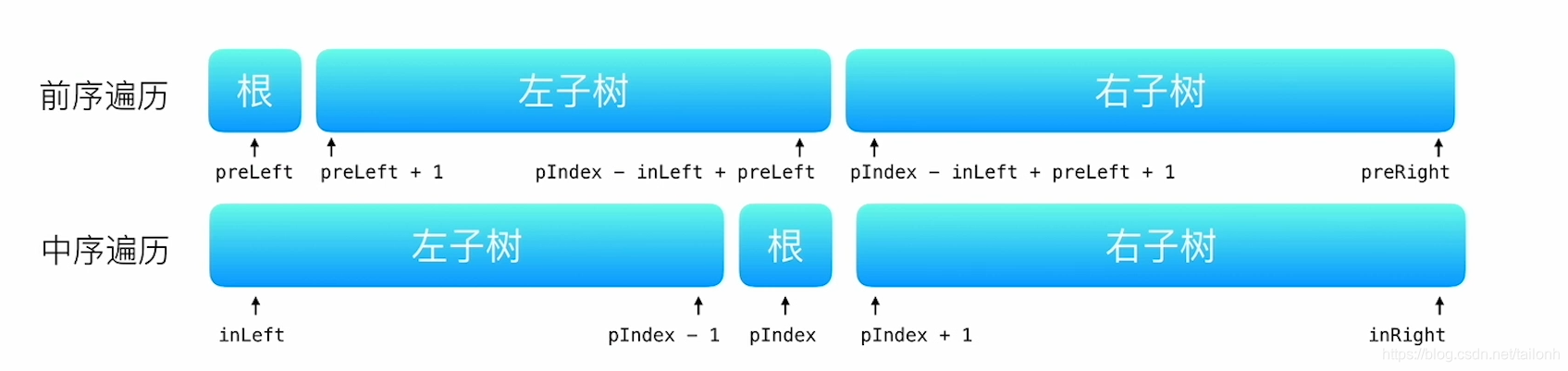
前序遍历和中序遍历的关键位置如下所示：

# Definition for a binary tree node.
# class TreeNode:
#     def __init__(self, x):
#         self.val = x
#         self.left = None
#         self.right = None

class Solution:
    def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:

        if inorder is None:
            return None
        # 前序遍历--递归方法构建树
        # 关键点在于，找到左、右子树的位置
        index = {}
        for i, v in enumerate(inorder):
            index[v]=i
        def tree(in_left, in_right, post_left, post_right):

            if in_left > in_right:
                return None
            # print(post_right)
            i_root = index[postorder[post_right]]
            
            left_tree_len = i_root-in_left
            root = TreeNode(postorder[post_right]) 
            # print(post_left+left_tree_len-1)
            root.left = tree(in_left, i_root-1, post_left, post_left+left_tree_len-1)

            root.right = tree(i_root+1, in_right, post_left+left_tree_len, post_right-1)


            return root
        n = len(inorder)
        return tree(0, n-1, 0, n-1)