需求描述
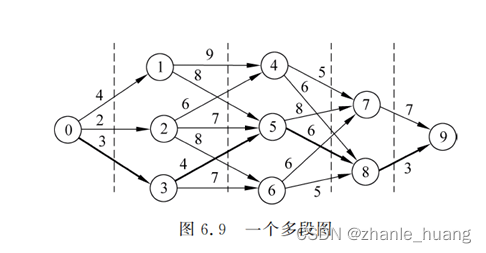
如图,在一个无环有向图中,找到起点0到终点的最短路径
实现思路
- 设s1,s2,…, st 是一条最短路径
- 假设s1,s2,已求出,则 s1,s2,…,st的问题则为 s2,…,st的问题
- 以此类推,可以将一条最短路径划分成多个子路径来求解
- 设公式 d(s, v) = Csv 为从s到v的权值为Csv
- 根据子问题的解的最小值即问题的最小值得出
- d(s, v) = min{d(s, u) + Cuv}
- 采用邻接矩阵来存储图数据
- 使用两个以为数组分别存储边的权值和路径,路径表示能到达当前下标的节点的点最小的权值的点
- 当将数据处理完后会得到如下表:

- 回溯即可得到路径
代码实现
// 图的最短路径问题
// 1.设s1,s2,..., st 是一条最短路径
// 2. 假设s1,s2,已求出,则 s1,s2,...,st的问题则为 s2,...,st的问题
// 因此,可以划分子问题 1、d(s,v) = Csv(表示从点s到点v的最短距离),最小距离公式2、d(s, v) = min{d(s, u) + Cuv}
#include <iostream>
using namespace std;
int arc[9][9];
const int MAX = 1000; // 设置最大权值不会超过1000
// 节点个数,起点下标,终点下标
int shortPath(int n, int end) {
int i, j;
int len[n], path[n];
// 初始化
for (i = 1; i < n; i++) {
len[i] = MAX;
path[i] = -1;
}
// 设置起点
len[0] = 0;
path[0] = -1;
// 当前待处理顶点,终点
for (j = 1; j < n; j++) {
// 其他顶点到待处理顶点,起点
for (i = j-1; i >= 0; i--) {
// 公式2取最小值,len[j]表示目前节点的路径长度值
if (len[i] + arc[i][j] < len[j]) {
// 比之前的小,重新存储更小的
len[j] = len[i] + arc[i][j];
// 到节点j最近的节点i时,0-j取最短距离
path[j] = i;
}
}
}
cout<<"输出终点"<<end;
i = end;
while(path[i] >= 0) {
cout<<"<-"<<path[i];
// 向前走
i = path[i];
};
return len[end-1];
}
// 输出得到的矩阵
void showWeight(int n) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++)
cout<<arc[i][j]<<"\t";
cout<<endl;
}
}
int main() {
// 定义矩阵
int i, j, k, start, end;
int weight;
int N;
int count;
cout<<"输入边的数量和节点数量";
cin>>count>>N;
for (i = 0; i < N; i++)
for (j = 0; j < N; j++)
arc[i][j] = MAX;
// 初始化数据
for (k = 0; k < count; k++) {
cout<<"请输入边的两个顶点和权值";
cin>>i>>j>>weight;
arc[i][j] = weight;
}
showWeight(N);
cout<<"输入终点";
cin>>end;
shortPath(N, end);
return 0;
}
输出结果:
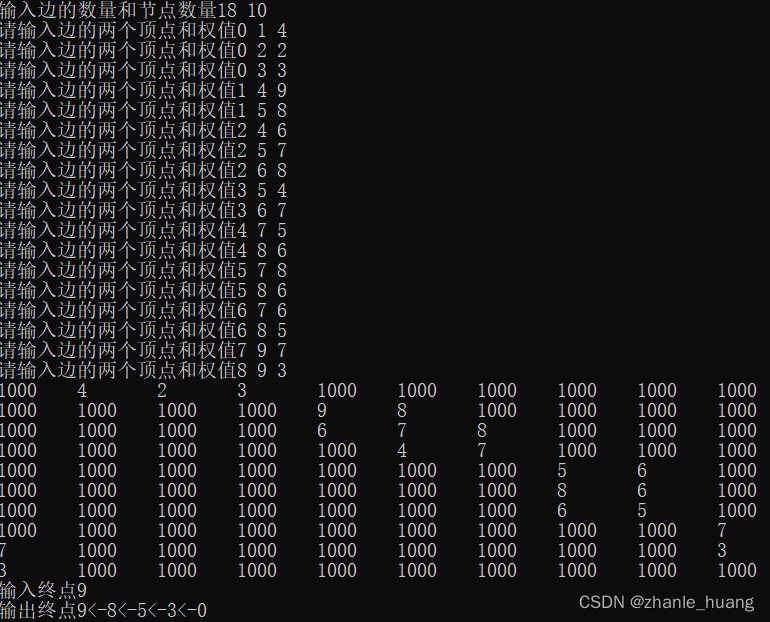








 该文章介绍了如何使用动态规划算法解决有向无环图(DAG)的最短路径问题,通过邻接矩阵存储图数据,并用C++编写代码实现。在代码中,初始化路径长度,然后通过迭代更新每个节点的最短路径,最终回溯得到最短路径。
该文章介绍了如何使用动态规划算法解决有向无环图(DAG)的最短路径问题,通过邻接矩阵存储图数据,并用C++编写代码实现。在代码中,初始化路径长度,然后通过迭代更新每个节点的最短路径,最终回溯得到最短路径。

















 4428
4428

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








