
来源:Deephub Imba
本文约4600字,建议阅读9分钟
本文将深入分析ViTAR相对于传统ViT的技术改进,重点阐述模糊位置编码的工作原理及其技术实现。视觉Transformer在计算机视觉领域展现出强大的性能,但其对输入图像尺寸的严格约束限制了在实际应用中的灵活性。ViTAR(Vision Transformer with Any Resolution)通过引入模糊位置编码技术,实现了对任意分辨率图像的处理能力,为计算机视觉的实际应用开辟了新的技术路径。
计算机视觉技术的快速发展中,视觉Transformer(ViT)作为重要的技术突破,在图像分类、目标检测等任务中取得了显著成果。传统ViT架构存在一个关键技术限制:要求所有输入图像具有统一的尺寸规格。这一约束在处理真实世界的多样化数据时带来了显著挑战,特别是在遥感图像、医学影像、监控视频等领域,图像数据往往具有不同的分辨率和宽高比。ViTAR通过创新的模糊位置编码机制,成功解决了这一技术瓶颈。
任意分辨率视觉Transformer的技术架构
ViTAR是一种新型的基于Transformer的视觉架构,其核心创新在于能够直接处理不同尺寸的图像数据,无需进行尺寸标准化或图像裁剪预处理。这一技术特性在需要保持原始空间信息完整性的应用场景中具有重要价值。
在传统的图像处理流程中,不同尺寸的图像数据需要通过缩放、裁剪等预处理操作统一到固定分辨率,这种处理方式可能导致关键空间信息的丢失。ViTAR通过技术创新避免了这一问题,其主要技术优势体现在:支持任意分辨率的图像输入、采用创新的模糊位置编码技术实现精确的空间位置感知、在高分辨率真实数据上保持稳定的性能表现。
ViTAR的技术特性使其在多个专业领域具有重要应用价值。在遥感图像处理中,该技术能够处理不同分辨率的卫星图像数据,确保地理信息的完整性和精度。在医学影像分析领域,ViTAR可以直接处理CT扫描、MRI或X射线图像的原始分辨率数据,避免因图像预处理导致的诊断信息丢失。在智能监控系统中,该技术能够适应不同摄像设备产生的多样化视频帧格式。此外,在文档分析和处理场景中,ViTAR能够有效处理不同格式和宽高比的扫描文档。
ViTAR采用多分辨率数据集进行训练,通过这种训练策略使模型学会在不同分辨率间进行有效泛化。这种训练方法使得ViTAR特别适合处理真实世界的复杂数据集,相比之下,传统ViT主要依赖于固定尺寸的标准化数据集(如ImageNet)进行训练。
技术对比分析
ViTAR与传统ViT在技术特性上存在显著差异。从灵活性角度分析,ViTAR提供了更高的输入适应性,能够处理任意分辨率的图像数据,而传统ViT则需要固定的输入尺寸。在性能表现方面,ViTAR在真实世界的高分辨率任务中表现出色,而传统ViT在处理标准化数据集时具有更好的计算效率。从实现复杂度来看,ViTAR的模糊位置编码机制增加了一定的技术复杂性,但传统ViT在处理统一标准化图像数据集时实现更为直接。

ViTAR的技术架构详解
ViTAR的技术架构体现了现代深度学习系统的设计理念,其核心组件包括以下几个关键模块:
首先是具有任意分辨率处理能力的补丁嵌入器。该模块将输入图像(无论是200×300像素还是4K分辨率)分割成固定尺寸的补丁(通常为16×16像素)。与传统方法不同,由于输入图像尺寸的变化,补丁的数量而非大小成为变量,这一设计保证了补丁内容的一致性。
其次是线性投影层,负责将每个图像补丁展平并通过线性变换,将原始像素数据转换为高维的补丁嵌入向量,为后续的Transformer处理做准备。
模糊位置编码模块是ViTAR的核心创新。为了准确跟踪每个补丁在原始图像中的空间位置,ViTAR引入了学习型插值位置向量,该向量能够随分辨率变化进行平滑缩放,确保模型在图像尺寸变化时仍能准确理解空间布局关系。
Transformer编码器模块采用多层堆叠结构,每层包含多头自注意力机制和多层感知机。这些组件并行处理所有补丁嵌入,实现全局信息交互。LayerNorm和残差连接机制确保训练过程的稳定性。
自适应聚合层根据不同任务需求进行特征整合。对于分类任务,采用特殊的CLS标记或全局平均池化生成单一的图像表示;对于密集预测任务如分割和检测,补丁输出被重新组织成空间网格形式。
最后的任务特定输出头根据具体应用需求进行设计,可以是简单的线性分类器、复杂的分割解码器或目标检测头。
传统ViT位置编码机制
位置嵌入的数学原理
传统Transformer架构中的正弦-余弦位置编码公式为14×14补丁网格(对应224×224像素图像,补丁大小16×16)构建位置嵌入提供了数学基础。该网格总共包含196个补丁(14×14=196,因为224/16=14)。
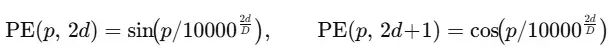
位置编码公式应用于ViT补丁索引p∈[0,195],其中嵌入维度D=768。这一编码机制的设计考虑了频率特性对空间位置感知的影响。
频率特性与空间感知
位置编码的频率特性决定了模型对空间细节的感知能力。低频通道在空间网格中变化平滑,而高频通道快速振荡,从而捕获精细的空间位置信息。
位置编码的数学表达式为:
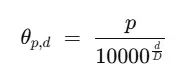
其中p表示补丁或标记的索引,d表示嵌入维度中的通道索引,D表示总的嵌入维度(如768)。
随着通道索引d的增加,分母10000^(d/D)呈指数增长,这导致角度变化率的递减,进而使得正弦/余弦值在相邻补丁间的变化速度逐渐放缓。
这一设计产生了重要的技术效果:低索引通道(如0、1)表现出快速振荡特性,对应高频空间信息;高索引通道(如510、511等)变化缓慢,对应低频空间信息。
为了验证这一频率特性,我们通过Python代码进行实验分析:
def plotSinusoid(d,k=14,D=768, n=10000): # k: 网格索引范围 # D: 嵌入维度 # d: 当前通道索引 K = np.arange(0, k, 1) denominator = np.power(n, 2*d/D) y = np.sin(K/denominator) plt.plot(K, y) plt.title('d = ' + str(d)) plt.xlabel('Patch Index') plt.ylabel('PE') fig = plt.figure(figsize=(8, 4)) ax1 = plt.subplot(311) plotSinusoid(0*100) for i in range(1, 3): # 创建共享x轴的子图以便比较不同频率特性 plt.subplot(311 + i, sharex=ax1) plotSinusoid(i*100) plt.tight_layout()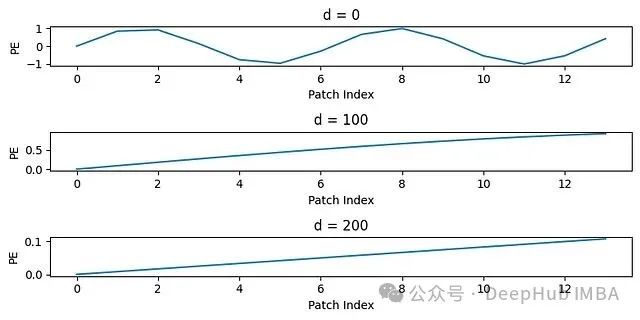
通过更详细的实验,我们可以深入理解位置编码的工作机制:
import numpy as np import matplotlib.pyplot as plt import math #------------- # ----------------------------------------------------------- H = W = 14 # 14×14网格对应196个补丁(224像素图像/16像素补丁=14) PATCHES = H * W # ----------------------------------------------------------- # 1) 补丁索引可视化(便于理解一维索引到二维网格的映射) # ----------------------------------------------------------- patch_idx = np.arange(PATCHES).reshape(H, W) plt.figure(figsize=(4,4)) plt.imshow(patch_idx, cmap="viridis") for y in range(H): for x in range(W): plt.text(x, y, patch_idx[y, x], ha='center', va='center', color='white', fontsize=6) plt.title("ViT Patch Indices (14×14)") plt.axis('off'); plt.tight_layout(); plt.show() # ----------------------------------------------------------- # ViT-Base配置参数(224×224图像,16×16补丁) # ----------------------------------------------------------- H = W = 14 # 补丁网格尺寸:14×14=196个补丁 D = 768 # ViT-Base标准嵌入维度 # 行主序扁平化补丁索引p∈[0, 195] p_flat = np.arange(H * W) # 形状:(196,) # ----------------------------------------------------------- # 1) 构建完整的正弦-余弦位置编码表(196×768) # ----------------------------------------------------------- pos_embed = np.zeros((H * W, D), dtype=np.float32) for d in range(0, D, 2): # 步长为2,处理正弦-余弦对 div_term = 10000 ** (d / D) # 频率调制因子 pos_embed[:, d] = np.sin(p_flat / div_term) pos_embed[:, d + 1] = np.cos(p_flat / div_term) # 重新组织为三维网格形式以便可视化分析:(H, W, D) pos_grid = pos_embed.reshape(H, W, D) # ----------------------------------------------------------- # 2) 低频通道可视化(d=0) # ----------------------------------------------------------- plt.figure(figsize=(4,3)) plt.imshow(pos_grid[..., 0], cmap="twilight") # 通道0对应正弦函数,表现出平滑特性 plt.title("Channel 0 (sin, lowest frequency)") plt.colorbar(); plt.axis('off'); plt.tight_layout(); plt.show() # ----------------------------------------------------------- # 3) 高频通道可视化(d≈D/2) # ----------------------------------------------------------- hi_d = D // 2 # 中等频率通道,展现快速变化特性 plt.figure(figsize=(4,3)) plt.imshow(pos_grid[..., hi_d], cmap="twilight") plt.title(f"Channel {hi_d} (sin, high frequency)") plt.colorbar(); plt.axis('off'); plt.tight_layout(); plt.show() # ----------------------------------------------------------- # 4) 不同行的正弦-余弦值变化曲线分析 # # ----------------------------------------------------------- rows = [0, 5, 10] plt.figure(figsize=(8,4)) for r in rows: plt.plot(pos_grid[r, :, 0], marker='o', label=f'sin row {r}') plt.plot(pos_grid[r, :, 1], marker='x', linestyle='--', label=f'cos row {r}') plt.title("Low-Frequency Positional Values along X-axis\n(rows 0, 5, 10 – channels 0 & 1)") plt.xlabel("Patch index along row (0 → 13)") plt.ylabel("Embedding value") plt.grid(True); plt.legend(fontsize=8, ncol=2); plt.tight_layout(); plt.show() # ---------------- 技术原理说明 ---------------- # • 通道0和1表现出平滑的空间变化特性:相邻补丁的编码值差异较小 # • 不同行(0、5、10)的曲线存在相位偏移,这是因为扁平索引 # p在每次向下移动一行时增加W(=14)个位置 # • 高频通道在14个位置步长内产生多次振荡, # 为模型提供精细的空间分辨率信息以支持注意力机制 # # ViT通过学习每个补丁的像素线性投影,然后将这个768维位置向量 # 与补丁特征相加,在第一个Transformer层之前为模型提供空间位置信息。 # 自注意力机制因此能够推理每个补丁的空间位置关系, # 即使输入被展平为一维序列形式。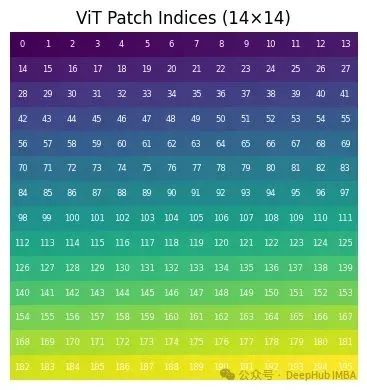
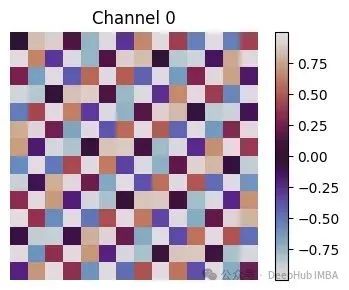
传统ViT位置嵌入的实践计算
以下实验展示了传统ViT如何将二维补丁坐标转换为可学习的向量表示,以及这些向量如何与补丁特征进行融合。
该过程包含三个关键步骤:首先,ViT将14×14的二维网格展平为196元素的一维序列;其次,参数张量pos_embed为CLS标记和每个补丁存储对应的768维向量;最后,模型通过简单的向量加法将pos_embed的相应行与每个补丁的投影像素特征相结合,为自注意力机制提供空间位置感知能力。
需要注意的关键技术限制是:如果输入图像尺寸不是标准的224×224(即补丁网格不是14×14),位置编码表将无法正确匹配,这时需要对图像进行尺寸调整或对pos_embed进行插值处理(正如ViTAR所采用的方案)。
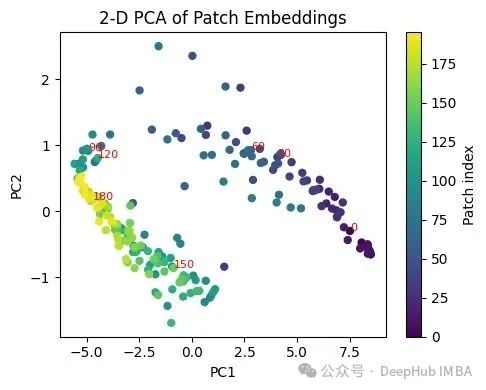
import matplotlib.pyplot as plt import numpy as np import torch import requests from PIL import Image from torchvision import transforms # 实验配置参数 img_size = 224 patch_size = 16 embed_dim = 768 # 加载真实图像数据进行实验 url = "https://images.unsplash.com/photo-1503023345310-bd7c1de61c7d?auto=format&fit=crop&w=224&h=224" img = Image.open(requests.get(url, stream=True).raw).convert("RGB") img_tensor = transforms.ToTensor()(img) # 张量形状: (3, 224, 224) # 图像补丁分割处理 patches = img_tensor.unfold(1, patch_size, patch_size).unfold(2, patch_size, patch_size) patches = patches.permute(1, 2, 0, 3, 4).reshape(-1, 3*patch_size*patch_size) # 形状: (196, 768) # 模拟ViT补丁嵌入器的线性投影过程 proj = torch.nn.Linear(patches.size(1), embed_dim, bias=False) with torch.no_grad(): patch_embeds = proj(patches) # 输出形状: (196, 768) # 通过主成分分析进行补丁嵌入的二维可视化 from sklearn.decomposition import PCA pca = PCA(n_components=2) coords_2d = pca.fit_transform(patch_embeds.numpy()) # 可视化1:显示补丁网格划分的原始图像 plt.figure(figsize=(4,4)) plt.imshow(img) ax = plt.gca() for i in range(0, img_size, patch_size): ax.axhline(i-0.5, color='white', linewidth=0.4) ax.axvline(i-0.5, color='white', linewidth=0.4) # 为便于理解,标注部分补丁的索引号 idx = 0 for r in range(14): for c in range(14): if (r == 0 and c % 3 == 0) or (c == 0 and r % 3 == 0): ax.text(c*patch_size+patch_size/2, r*patch_size+patch_size/2, str(idx), color='yellow', fontsize=6, ha='center', va='center') idx += 1 plt.title("224×224 Image with 16×16 Patch Grid") plt.axis('off') plt.tight_layout() plt.show() # 可视化2:196个补丁嵌入的二维主成分分析结果 plt.figure(figsize=(5,4)) plt.scatter(coords_2d[:,0], coords_2d[:,1], c=np.arange(196), cmap='viridis', s=25) for i in range(0,196,30): plt.text(coords_2d[i,0], coords_2d[i,1], str(i), color='red', fontsize=8) plt.title("2‑D PCA of Patch Embeddings") plt.xlabel("PC1") plt.ylabel("PC2") plt.colorbar(label="Patch index") plt.tight_layout() plt.show()
模糊位置编码
从刚性表格到弹性数学表面
传统视觉Transformer采用刚性的位置编码查找表,为224×224图像中的每个补丁存储固定的位置信息。当输入图像尺寸发生变化时,这种固定表格无法提供对应的位置编码,导致模型必须通过图像预处理来适应固定的输入尺寸。这种方法的局限性在于无法处理多样化的真实世界数据。
ViTAR通过引入模糊位置编码技术,将刚性的位置编码表格转换为连续的数学表面。这一创新使得当图像从14×14补丁网格扩展到24×24补丁网格时,ViTAR能够通过平滑的双三次插值在同一数学表面上采样新的位置编码点,而无需重新训练或调整网络架构。
连续函数插值的技术原理
ViTAR摒弃了传统的one-hot位置表示方法,转而学习一个能够插值到任意补丁网格的连续函数。其核心函数resample_abs_pos_embed通过在二维位置网格上执行双三次插值实现这一功能,该过程类似于图像尺寸调整,但操作对象是高维的嵌入空间。
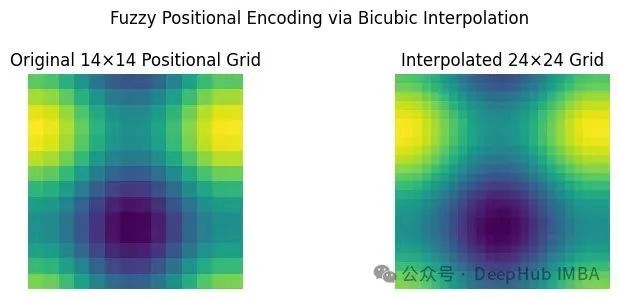
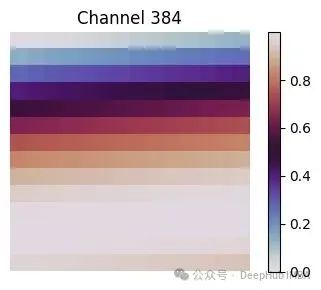
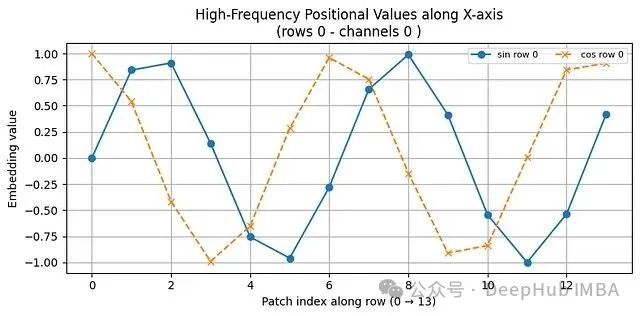
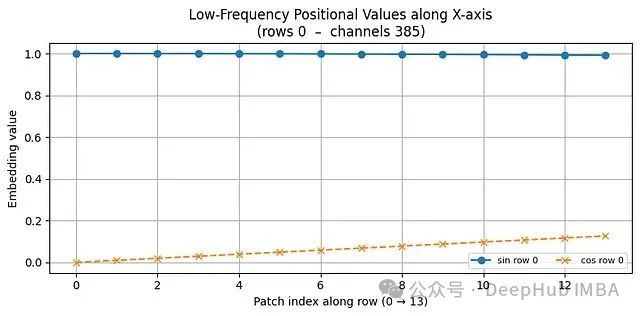
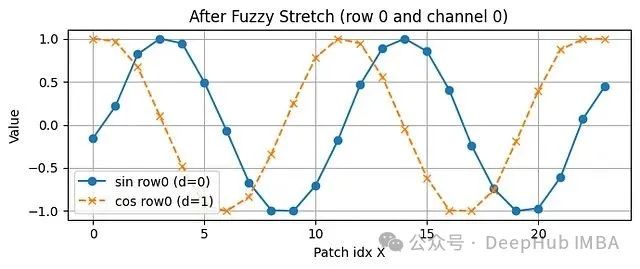
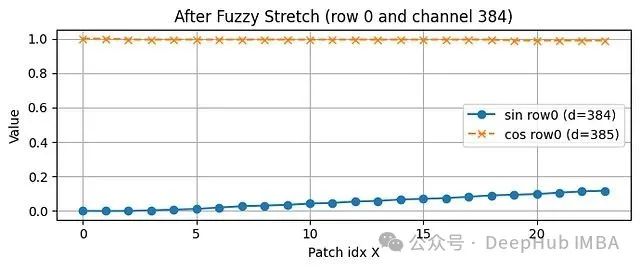
为了深入理解这一技术机制,我们通过实验对比传统ViT和ViTAR的位置编码处理方式。实验结果表明,低频通道在插值后保持平滑特性,而高频通道呈现条纹模式。重要的是,这一过程不会创造新的位置信息,而是通过模式拉伸的方式使ViTAR能够在更高分辨率下保持位置语义的一致性。
# ----------------------------------------------------------- # 0) 实验配置——ViT-Base(16像素补丁,224×224图像对应14×14网格) # ----------------------------------------------------------- H0 = W0 = 14 # 原始补丁网格尺寸 D = 768 # 嵌入空间维度 # 工具函数:根据Transformer位置编码公式生成正弦-余弦编码对 def build_sincos_table(H, W, D): p_flat = np.arange(H * W) # 行主序补丁索引 table = np.zeros((H * W, D), np.float32) for d in range(0, D, 2): angle = p_flat / 10000 ** (d / D) table[:, d] = np.sin(angle) table[:, d + 1] = np.cos(angle) return table.reshape(H, W, D) # 输出形状: (H, W, D) pos14 = build_sincos_table(H0, W0, D) # 生成标准14×14位置编码表 # ----------------------------------------------------------- # 1) 补丁索引空间分布可视化 # ----------------------------------------------------------- patch_idx = np.arange(H0*W0).reshape(H0, W0) plt.figure(figsize=(4,4)) plt.imshow(patch_idx, cmap="viridis") for y in range(H0): for x in range(W0): plt.text(x, y, patch_idx[y,x], ha='center', va='center', color='white', fontsize=6) plt.title("Patch Indices 14×14"); plt.axis('off'); plt.tight_layout(); plt.show() # ----------------------------------------------------------- # 2) 模糊位置编码插值处理(ViTAR核心技术) # 对每个编码通道进行图像式的双三次上采样 # ----------------------------------------------------------- H1 = W1 = 24 # 目标网格尺寸,对应384×384像素图像 pos24 = np.zeros((H1, W1, D), np.float32) for d in range(D): # 通道数据标准化处理:映射到0-255范围,便于PIL图像处理 ch = pos14[..., d] ch_img = Image.fromarray(((ch - ch.min()) / np.ptp(ch) * 255).astype(np.uint8)) ch_up = ch_img.resize((W1, H1), Image.Resampling.BICUBIC) # 反标准化:恢复原始数值范围 ch_up = np.asarray(ch_up).astype(np.float32) / 255 * np.ptp(ch) + ch.min() pos24[..., d] = ch_up # ----------------------------------------------------------- # 3) 低频通道插值效果对比分析 # ----------------------------------------------------------- fig, ax = plt.subplots(1,2, figsize=(7,3)) ax[0].imshow(pos14[...,0], cmap="twilight"); ax[0].set_title("d=0 (14×14)"); ax[0].axis('off') ax[1].imshow(pos24[...,0], cmap="twilight"); ax[1].set_title("d=0 (24×24 – fuzzy)"); ax[1].axis('off') plt.suptitle("Channel Stretches Smoothly"); plt.tight_layout(); plt.show() # ----------------------------------------------------------- # 4) 高频通道插值效果对比分析 # ----------------------------------------------------------- hi = D//2 fig, ax = plt.subplots(1,2, figsize=(7,3)) ax[0].imshow(pos14[...,hi], cmap="twilight"); ax[0].set_title(f"d={hi} (14×14)") ax[1].imshow(pos24[...,hi], cmap="twilight"); ax[1].set_title(f"d={hi} (24×24 – fuzzy)") for a in ax: a.axis('off') plt.suptitle("Channel Keeps Pattern (more stripes)"); plt.tight_layout(); plt.show() # ----------------------------------------------------------- # 5) 特定行的高频通道数值变化曲线 # # ----------------------------------------------------------- row = 0 plt.figure(figsize=(7,3)) plt.plot(pos24[row,:,hi], 'o-', label=f'sin row0 (d={hi})') plt.plot(pos24[row,:,hi+1], 'x--', label=f'cos row0 (d={hi+1})') plt.grid(True); plt.xlabel("Patch idx X"); plt.ylabel("Value") plt.title(f"After Fuzzy Stretch (row 0 and channel {hi})") plt.legend(); plt.tight_layout(); plt.show() # ----------------------------------------------------------- # 6) 特定行的低频通道数值变化曲线 # ----------------------------------------------------------- plt.figure(figsize=(7,3)) plt.plot(pos24[row,:,0], 'o-', label='sin row0 (d=0)') plt.plot(pos24[row,:,1], 'x--', label='cos row0 (d=1)') plt.grid(True); plt.xlabel("Patch idx X"); plt.ylabel("Value") plt.title("After Fuzzy Stretch (row 0 and channel 0)") plt.legend(); plt.tight_layout(); plt.show() # --------------------- 技术要点总结 --------------------------- # • 模糊编码的本质是对每个编码通道进行图像式的双三次插值调整 # • 低频通道在插值后保持平滑的空间连续性;高频通道保持原有的振荡模式 # • 插值过程不产生新的位置信息,而是通过模式拉伸的方式 # 使ViTAR能够在更高分辨率下维持位置编码的语义一致性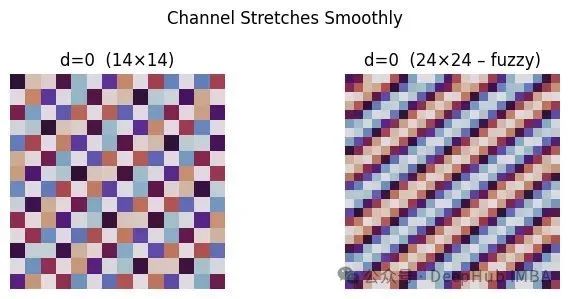

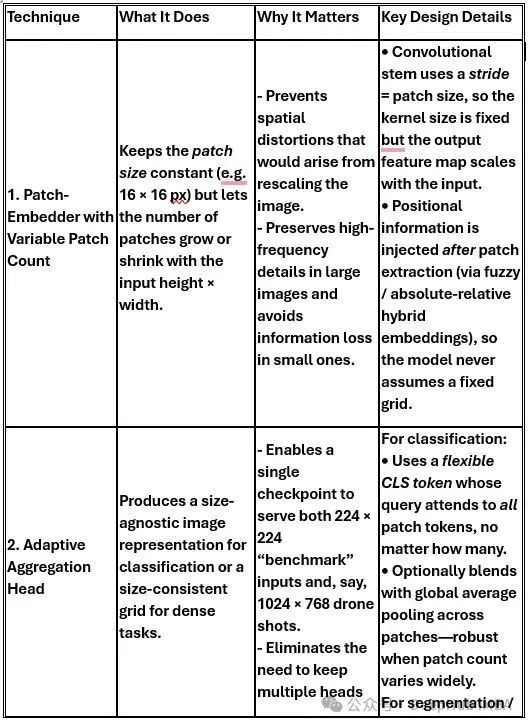
ViTAR的技术优化策略
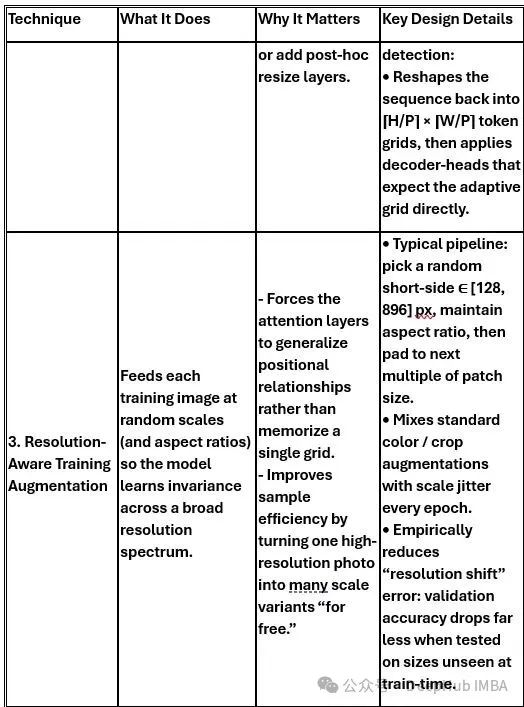
除了核心的模糊位置编码技术,ViTAR还集成了多项技术优化策略,以确保在处理可变尺寸图像时保持系统的稳定性和性能。
总结
ViTAR代表了视觉Transformer技术的重要进步,特别是在处理多样化和高分辨率图像数据的应用场景中表现出显著优势。该技术通过模糊位置编码的创新机制实现了输入尺寸的灵活性,保持了空间细节信息的完整性,同时避免了传统模型在预处理阶段的复杂操作。
对于需要处理真实世界复杂视觉数据的应用场景,ViTAR提供了一个技术上更为先进和实用的解决方案。其在保持计算效率的同时实现了对任意分辨率图像的有效处理,为计算机视觉技术在更广泛领域的应用奠定了坚实的技术基础。
编辑:王菁
关于我们
数据派THU作为数据科学类公众号,背靠清华大学大数据研究中心,分享前沿数据科学与大数据技术创新研究动态、持续传播数据科学知识,努力建设数据人才聚集平台、打造中国大数据最强集团军。

新浪微博:@数据派THU
微信视频号:数据派THU
今日头条:数据派THU























 7472
7472

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








