深度学习简介：第 1 部分

尽管深度学习作为人工智能的一个分支，最近才变得突出，但它是基于化学工程师熟悉的概念。本文介绍人工神经网络——支持深度学习的算法。

中国古代围棋游戏的可能走法比宇宙中原子的数量还要多。与国际象棋不同，围棋无法通过强力计算能力来分析大量的走法来获胜——可能性太多了。而且，与国际象棋不同，围棋获胜的策略不能用规则来有意义地编纂：它的原则是神秘的。在某些文化中，围棋被视为人类通过直觉实例与神的联系的一种方式，通过“不知道如何知道的情况下就知道”。

专家们认为，即使有的话，计算机几十年内也无法在围棋比赛中击败顶级人类棋手。但在 2016 年，一个名为 AlphaGo 的计算机程序击败了围棋传奇世界冠军李世石(1)。在比赛过程中，AlphaGo 发挥了高度的创造力，做出了人类从未做过的棋步，并以 4 比 1 击败了 18 届世界冠军。

AlphaGo 是一种使用深度学习技术构建的人工智能 (AI) 程序。从自动驾驶汽车到律师机器人(2)，深度学习正在推动许多人认为将是世界上最大的技术革命。“就像 100 年前电力几乎改变了一切一样，我实际上很难想象人工智能在未来几年内不会改变一个行业，”曾担任斯坦福人工智能实验室主任、百度首席科学家和谷歌大脑创始人的吴恩达 (Andrew Ng) 说道。

化学工程师通常使用计算机对化学过程进行建模、模拟、设计和优化。通常，计算方法是使用 Excel、MatLab、AspenPlus、CHEMCAD、COMSOL Multiphysics 等软件工具执行的数值算法（即回归、统计、微分方程等）。所有这些方法和工具都是众所周知的化学工程原理的应用，工程师将其巧妙地组合和应用来解决高级问题。计算机能否做的不仅仅是计算，并且有朝一日能像化学工程师一样解决高级问题？

“我们的愿景是，你将能够走到一个系统前说，‘我想制造这个分子。’” 软件会告诉你应该从哪条路线制造，然后机器就会制造出来，”麻省理工学院化学工程沃伦·K·刘易斯 (Warren K. Lewis) 教授 Klavs Jensen 说道(3)。他的研究利用深度学习来确定将一组可用反应物转化为目标化合物的途径(4)。在学术界之外，深度学习已经被实践工程师用来解决一系列以前棘手的问题，并且未来对于化学工程师来说可能会像 Excel 一样有价值。

什么是深度学习？

▲图 1.机器学习是人工智能的一个分支，它赋予计算机无需编程的学习能力。深度学习是机器学习的一个子领域。

人工智能是机器模仿人类智能行为的能力（图1）。机器学习 (ML) 是人工智能的一个分支，它使计算机能够“学习”（通常是从数据中），而无需进行显式编程。深度学习是机器学习的一个子领域，它使用称为人工神经网络 (ANN) 的算法，该算法受到大脑结构和功能的启发，并且能够进行自学习。人工神经网络被训练来“学习”模型和模式，而不是被明确告知如何解决问题。

人工神经网络的构建模块称为感知器，它是一种受生物神经元启发的算法(5)。尽管感知器是在 1957 年发明的，但直到最近，人工神经网络仍然默默无闻，因为它们需要大量的训练，而获得有用结果的训练量超出了可用的计算机能力和数据大小。

要了解最近计算能力的增长，请考虑一下 2012 年 Google Brain 项目必须使用一台消耗 600 千瓦电力、成本约为 5,000,000 美元的定制计算机。到 2014 年，斯坦福人工智能实验室通过使用三台现成的图形处理单元 (GPU) 加速服务器获得了更多的计算能力，每台服务器的成本约为 33,000 美元，仅消耗 4 千瓦的电力。如今，您可以花 80 美元购买一款专门的神经计算棒，它可以提供超过 100 gigaflops 的计算性能。

感知器

▲图 2.人类神经元使用树突收集其他神经元的输入并对所有输入求和。如果总数大于阈值，则会产生输出。

人脑平均约有 1000 亿个神经元。人类神经元使用树突收集来自其他神经元的输入，将所有输入相加，如果所得总和大于阈值，它就会触发并产生输出。然后，激发的输出被发送到其他连接的神经元（图 2）。

▲图 3。感知器是神经元的数学模型。它接收加权输入，将这些输入相加并传递给激活函数。激活函数决定是否应该产生输出。

感知器是生物神经元的数学模型(6)。就像真正的神经元一样，它接收输入并计算输出。每个输入都有一个相关的权重。所有输入都单独乘以其权重，相加，然后传递到激活函数，该函数确定神经元是否应该激发并产生输出（图 3）。

有许多不同类型的激活函数具有不同的属性，但最简单的之一是阶跃函数(7)。如果输入高于某个阈值，阶跃函数将输出 1，否则输出 0。例如，如果感知器有两个输入（x 1和x 2）：

x 1 = 0.9

x 2 = 0.7

其权重（w 1和w 2）为：

w 1 = 0.2

w 2 = 0.9

激活函数阈值等于 0.75，然后对输入进行加权并将它们相加得出：

x 1 w 1 + x 2 w 2 = (0.9×0.7) + (0.2×0.9) = 0.81

由于总输入高于阈值 (0.75)，神经元将放电。由于我们选择了一个简单的阶跃函数，因此输出将为 1。

那么这一切是如何导致智力的呢？它始于通过培训学习简单事物的能力。

训练感知器

▲图 4。为了训练感知器，调整权重以最小化输出误差。输出误差定义为期望输出与实际输出之间的差异。

训练感知器需要为其提供多个训练样本并计算每个训练样本的输出。每次采样后，都会调整权重以最小化输出误差，通常定义为期望（目标）与实际输出之间的差异（图 4）。

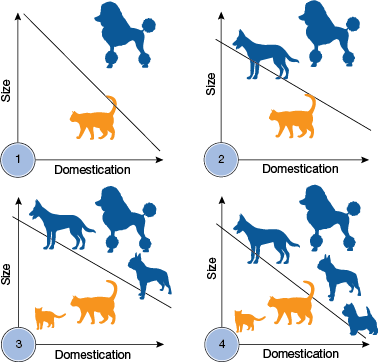
▲图 5。感知器可以根据体型和驯化数据学习区分狗和猫。随着更多训练示例的添加，感知器更新其线性边界。

通过遵循这个简单的训练算法来更新权重，感知器可以学习执行二元线性分类。例如，如果数据可线性分类，它可以在给定大小和驯化数据的情况下学习将狗与猫分开（图 5）。

感知器学习分类的能力非常重要，因为分类是许多智能行为的基础。分类的一个常见示例是检测垃圾邮件。给定一个训练数据集，其中包含标记为“垃圾邮件”的类似垃圾邮件的电子邮件和标记为“非垃圾邮件”的常规电子邮件，一种可以学习垃圾邮件特征的算法将非常有用。同样，此类算法可以学习将肿瘤分类为癌性或良性，了解您的音乐偏好并将歌曲分类为“可能喜欢”和“不太可能喜欢”，或者学习区分正常行为的瓣膜和异常行为的瓣膜 (8 )。

感知器是强大的分类器。然而，单独而言，它们只能学习线性可分类模式，而无法处理非线性或更复杂的模式。

多层感知器

单个神经元能够学习简单的模式，但是当许多神经元连接在一起时，它们的能力会急剧增强。人脑中 1000 亿个神经元中的每一个平均与其他神经元有 7000 个连接。据估计，三岁儿童的大脑神经元之间约有一万亿个连接。而且，从理论上讲，大脑中可能存在的神经连接比宇宙中的原子还要多。

▲图 6。多层感知器在输入和输出之间有多层神经元。每个神经元的输出都连接到下一层中的每个神经元。

多层感知器 (MLP) 是一种人工神经网络，在输入和输出之间具有多层神经元。MLP 也称为前馈神经网络。前馈是指数据从输入层沿一个方向流向输出层。通常，每个神经元的输出都连接到下一层中的每个神经元。输入层和输出层之间的层称为隐藏层（图 6）。

▲图 7。虽然单个感知器可以学习对线性模式进行分类，但它们无法处理非线性或其他更复杂的数据集。多层感知器更能够处理非线性模式，甚至可以对不可分离的数据进行分类。

MLP 广泛用于模式分类、识别、预测和近似，并且可以学习使用线性或其他容易表达的曲线不可分离的复杂模式。MLP 网络学习复杂模式的能力随着神经元和层数的增加而增加（图 7）。

▲图 8.用于识别支票上打印的数字的多层感知器将具有一个输入网格来读取数字的各个像素，然后是一层或多层隐藏神经元，以及 10 个输出神经元来指示识别了哪个数字。

MLP 在广泛的人工智能任务中取得了成功，从语音识别(9)到预测电解质水溶液的热导率(10)和控制连续搅拌釜反应器(11)。例如，用于识别印刷数字（例如，支票上印刷的帐户和路由号码）的 MLP 将由输入网格组成，用于读取数字的各个像素（例如，9×12 位图），后面是一个或多个隐藏层，最后是 10 个输出神经元，用于指示在输入 (0-9) 中识别了哪个数字（图 8 ）。

这种用于识别数字的 MLP 通常会通过向其显示数字图像并告诉它是否正确识别它们来进行训练。最初，MLP 的输出是随机的，但随着训练的进行，它将调整神经元之间的权重并开始正确对输入进行分类。

现实生活中用于识别手写数字的典型 MLP 由 784 个感知器组成，这些感知器接受来自表示手写数字的 28×28 像素位图的输入、隐藏层中的 15 个神经元和 10 个输出神经元 (12 )。通常，此类 MLP 是使用 50,000 个手写数字标记图像池进行训练的。在配置良好的计算机上经过几分钟的训练后，它可以学会识别以前未见过的手写数字，准确率达到 95%。

以类似的方式，其他人使用Perry 化学工程师手册中的数据来训练 MLP 来预测化合物的粘度(13)。在另一项研究中，科学家能够通过训练 MLP 识别温度和流量偏差作为换热器内部管道堵塞和部分污垢的症状来检测换热器中的故障 (14 )。

▲图 9. MLP 可以通过评估实际被控对象输出与神经网络输出之间的误差来学习被控对象的动态。

▲图 10.通过使用有关流入、浓度、液位和流出的过去数据，可以对连续搅拌釜反应器进行训练，以保持适当的产品浓度和流量。

另一个例子是，MLP 已用于化学反应器的预测控制(15)。典型的设置训练神经网络来学习植物的前向动态。工厂输出和神经网络输出之间的预测误差用于训练神经网络（图9）。神经网络从先前的输入和输出中学习，以预测工厂输出的未来值。例如，可以使用有关浓度C b 1 和 Q 2 的流入量 Q 1和Q 2的过去数据来训练催化连续搅拌釜反应器（图 10 ）的控制器，以维持适当的产品浓度和流量。C b 2分别为浓度C b处的液位h和流出量Q 0。

一般来说，给定一个统计相关的数据集，人工神经网络可以从中学习(16)。

训练多层感知器

训练单个感知器很容易——所有权重都会反复调整，直到输出与所有训练数据的预期值匹配。对于单个感知器，可以使用以下公式调整权重：

其中w i是权重，Δ w i是权重调整，t是目标输出，o是实际输出，η 是学习率——通常是一个用于调节权重变化率的小值。

然而，这种独立调整每个权重的方法不适用于 MLP，因为每个神经元的输出都是下一层中所有神经元的输入。调整一个连接的权重不仅会影响它直接传播到的神经元，还会影响后续层中的所有神经元，从而影响所有输出。因此，您无法通过一次优化一个权重来获得一组最佳权重。相反，必须同时搜索可能的权重组合的整个空间。实现此目的的主要方法依赖于一种称为梯度下降的技术。

想象一下，您位于山顶，并且需要以最快的方式到达山底。一种方法可能是向各个方向观察，看看哪条路的坡度最陡，然后朝那个方向迈进。如果你重复这个过程，你就会逐渐走下坡路。这就是梯度下降的工作原理：如果您可以在所有权重上定义一个反映期望输出和计算输出之间差异的函数，那么当 MLP 的输出与期望输出匹配时，该函数将是最低的（即山底）。朝着这个最低值移动将变成计算梯度（或函数的导数）并在梯度方向上迈出一小步的问题。

反向传播是“误差反向传播”的缩写，是使用梯度下降训练 MLP 的最常用算法。名称的后向部分源于梯度的计算通过网络向后进行的事实。先计算最后一层权重的梯度，最后计算第一层权重的梯度。

▲图 11. Sigmoid 和 tanh 函数是非线性激活函数。sigmoid 函数的输出是 0 到 1 之间的值。sigmoid 函数的输出可用于表示概率，通常是输入属于某个类别（例如猫或狗）的概率。

在了解反向传播如何工作之前，请回想一下感知器计算其输入的加权和，然后决定是否应该触发。是否触发的决定由激活函数决定。在感知器示例中，我们使用阶跃函数，如果输入高于某个阈值，则输出 1，否则输出 0。在实践中，人工神经网络使用非线性激活函数，如 sigmoid 或 tanh 函数（图 11），至少部分原因是简单的阶跃函数不适合计算梯度 - 它的导数为0。

sigmoid 函数将其输入映射到 0 到 1 的范围。您可能还记得，概率也由 0 到 1 之间的值表示。因此，sigmoid 函数的输出可用于表示概率 - 通常是输入属于某个类别（例如，猫或狗）的概率。因此，它是人工神经网络中使用最广泛的激活函数之一。

示例：使用反向传播训练 MLP

▲图 12。具有三层的 MLP 示例接受 [1, 1] 输入并计算输出 0.77。

考虑一个具有三层的简单 MLP（图 12）：输入层中的两个神经元 ( X i 1、X i 2 ) 通过权重W 1 – W 6连接到隐藏层中的三个神经元 ( X h 1、X h 2、X h 3 )，这些神经元通过权重W 7 – W 9连接到单个输出神经元 ( X o )。假设我们使用 sigmoid 激活函数，初始权重是随机分配的，输入值 [1, 1] 将导致输出为 0.77。

假设输入 [1, 1] 的期望输出为 0。反向传播算法可用于调整权重。首先，计算最后一个神经元 ( X o ) 输出的误差：

回想一下，输出 (0.77) 是通过将 sigmoid 激活函数应用于前一层输出 (1.2) 的加权和而获得的：

σ(1.2) = 1/(1 + e –1.2 ) = 0.77

sigmoid 函数的导数表示梯度或变化率：

因此，sigmoid 函数在x = 1.2处的梯度或变化率为： (0.77) × (1 – 0.77) = 0.177

如果我们将输出误差 (–0.77) 乘以该变化率 (0.177)，我们会得到 –0.13。这可以被认为是输入的一个小变化，可以将系统推向众所周知的“山底”。

回想一下，输出神经元的加权输入之和（1.2）是前一层中三个神经元的输出以及它们与输出神经元之间的权重的乘积：

要将总和 ( S o ) 更改 –0.13，我们可以调整每个传入权重 ( W 7、W 8、W 9 )，使其与前一个（隐藏层）神经元的相应输出 ( X h 1、X h 2、X h 3 )成比例。因此，隐藏神经元和输出神经元之间的权重变为：

W 7新= W 7旧+ (–0.13/ X h 1 ) = 0.3 + (–0.13/0.73) = 0.11

W 8新= W 8旧+ (–0.13/ X h 2 ) = 0.5 + (–0.13/0.79) = 0.33

W 9新= W 9旧+ (–0.13/ X h 3 ) = 0.9 + (–0.13/0.67) = 0.7

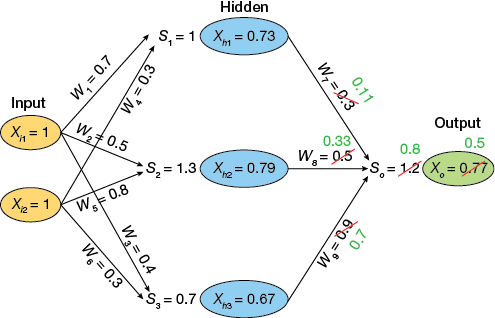
▲图13.使用反向传播算法调整隐藏层神经元和输出神经元之间的权重，使输出更接近目标值（0）。

调整隐藏层神经元和输出神经元之间的权重后（图13），我们重复该过程并类似地调整输入和隐藏层神经元之间的权重。这是通过首先计算进入隐藏层中每个神经元的输入的梯度来完成的。例如，X h 3处的梯度为：0.67×(1–0.67) = 0.22。

X h 3（即 S 3）的加权输入总和的建议变化可以通过将梯度（0.22）乘以后续神经元的加权输入总和的建议变化（–0.13），然后除以从该神经元到后续神经元的权重（W 9 ）来计算。请注意，我们正在向后传播误差，因此我们将后面的神经元 ( X o )中的误差按比例向后传播到该神经元的输入。

X h 3（即 S 3 ）的加权输入总和的建议变化为：

S 3的变化= X h 3处的梯度× S o / W 9的建议变化

S 3的变化= 0.22 × (–0.13)/0.9 = –0.03

请注意，我们使用W 9的原始值(0.9) 而不是最近计算的新值 (0.7) 来向后传播误差。这是因为，虽然我们一次一步地工作，但我们正在尝试搜索可能的权重组合的整个空间，并将它们更改为正确的方向（朝向山脚）。在每次迭代中，我们通过原始权重传播输出误差，从而产生新的迭代权重。输出神经元误差的全局反向传播是让所有权重向理想值变化的关键概念。

一旦您知道每个神经元（ S 1、S 2、S 3 ）输入的加权和的建议变化，您就可以与前一个神经元的输出成比例地更改通向该神经元的权重（W 1到W 6 ）。因此，W 6从0.3变为0.27。

对所有权重重复此过程后，此示例中的新输出变为 0.68，这比我们开始时的值 (0.77) 更接近理想值 (0)。通过执行一次这样的前向和反向传播迭代，网络就已经在学习了！

像本例中这样的小型神经网络通常会在数百次这样的权重调整迭代后学会产生正确的输出。另一方面，训练AlphaGo的神经网络有数万个神经元，分布在十几层中，需要更强大的计算能力，而这种计算能力正变得越来越可用。

期待

尽管人工智能领域取得了惊人的进步，例如自动驾驶汽车，但该技术的成就仍然非常有限，距离自动驾驶还很遥远。如今，99% 的机器学习需要人类工作和大量需要标准化和标记的数据（即，这是一只狗；这是一只猫）。而且，人们需要提供和微调适当的算法。这一切都依赖于体力劳动。

困扰神经网络的其他挑战包括：

• 偏见。机器学习正在寻找数据中的模式。如果你从糟糕的数据开始，你最终会得到糟糕的模型。
• 过拟合。一般来说，模型通常通过在特定训练数据集上最大化其性能来进行训练。因此，该模型会记住训练示例，但可能无法学习泛化到新情况和数据集。
• 超参数优化。超参数的值在学习过程开始之前定义（例如，层数、每层神经元数、激活函数类型、权重初始值、学习率值等）。少量更改此类参数的值可能会引起网络性能的大幅变化。
• 黑盒问题。神经网络本质上是黑匣子，研究人员很难理解它们如何推断出特定的结论。它们的操作对于人类来说基本上是不可见的，这使得它们不适合验证过程很重要的领域。

到目前为止，我们已经研究了从数据中学习的神经网络。这种方法称为监督学习。正如本文所讨论的，在监督学习下训练神经网络期间，向网络提供输入并产生与期望/目标输出进行比较的输出。如果实际输出和目标输出之间存在差异，则会产生误差，并根据该误差调整权重，直到实际输出与期望输出匹配。监督学习依赖于人工收集、准备和标记大量训练数据。

在本系列的第 2 部分中，我们将深入研究另外两种更自主的方法：无监督学习和强化学习。

无监督学习不依赖于学习的目标输出。相反，相似类型的输入被组合起来形成集群。当应用新的输入模式时，神经网络给出指示输入模式所属的类的输出。

强化学习涉及通过尝试和错误进行学习，仅通过奖励或惩罚来学习。这种神经网络直接从原始输入（例如视觉）构建和学习自己的知识，而不需要任何手工设计的特征或领域启发法。AlphaGo Zero 是 AlphaGo 的继承者，基于强化学习。与 AlphaGo 最初是通过数千种人类对弈来训练来学习如何下围棋不同，AlphaGo Zero 只是通过与自己对弈来学习下棋。尽管它一开始是完全随机的对弈，但它最终超越了人类的对弈水平，并以 100 比 0 击败了之前版本的 AlphaGo。

在第 2 部分中，我们还将研究一些奇特的神经网络架构，例如长短期记忆网络 (LSTM)、卷积神经网络 (CNN) 和生成对抗网络 (GAN)。

最后但并非最不重要的一点是，我们将讨论社会和伦理方面，因为人工智能最近的爆炸性进展引发了人们的担忧，即人工智能将从为人类社会造福演变为控制。就连英国最杰出的科学家之一史蒂芬·霍金也对人工智能的威胁发出了警告。“全面人工智能的发展可能意味着人类的终结，”霍金(17)说道。